Orantı için güven aralığı
Bu makalede orantı için güven aralığının ne olduğu ve istatistikte ne için kullanıldığı açıklanmaktadır. Benzer şekilde, oranın güven aralığını nasıl hesaplayacağınızı ve kavramı daha iyi anlamak için çözümlü bir alıştırmayı keşfedeceksiniz.
Oranın güven aralığı nedir?
Oran için güven aralığı, bir popülasyonun oranı için bir dizi kabul edilebilir değer sağlayan bir aralıktır. Yani orana ilişkin güven aralığı, nüfus oranının bir hata payı ile bu değerler arasında yer aldığı bir maksimum değeri ve bir minimum değeri belirtir.
Örneğin güven düzeyi %95 olan bir popülasyonun oranına ilişkin güven aralığı (0,73, 0,81) ise bu, bir popülasyonun oranının %95 olasılıkla %73 ile %81 arasında olduğu anlamına gelir.
Bu nedenle oranın güven aralığı, belirli özellikleri karşılayan bir popülasyonun oranının değerini tahmin etmek için kullanılır.
Bir sonraki bölümde göreceğimiz gibi orana ilişkin güven aralığı örneklem oranına ve örneklemdeki gözlem sayısına bağlıdır.
Oran için güven aralığı formülü
Oranın güven aralığı, Z α/2 değerinin örnek oranının kareköküyle (p) çarpılması, 1-p ile çarpılması ve örnek büyüklüğüne (n) bölünmesiyle örnek oranına eklenip çıkarılarak hesaplanır. Bu nedenle orana ilişkin güven aralığını hesaplama formülü şöyledir:

Altın:
-

örnek oranıdır.
-

örneklem büyüklüğüdür.
-

α/2 olasılığına karşılık gelen standart normal dağılımın niceliğidir. Büyük örneklem büyüklükleri ve %95 güven düzeyi için genellikle 1,96’ya, %99 güven düzeyi için ise genellikle 2,576’ya yakındır.
Oran için güven aralığı hesaplama örneği
Oran için güven aralığının nasıl hesaplandığını görebilmeniz için sizi adım adım somut bir örnekle aşağıda bırakıyoruz.
- Bir sigorta şirketi pazar araştırması yaparak bir ülkede kaç kişinin hayat sigortasına sahip olduğunu belirlemek istiyor. Bunun için rastgele 700 kişilik bir örneklem analiz ediliyor ve örneklemin %40’ının hayat sigortası olduğu sonucuna ulaşıyoruz. Ülke nüfusunun oranı için %95 güven düzeyinde güven aralığı nedir?
Popülasyon oranının güven aralığını belirlemek için yukarıda gördüğümüz formülü kullanmamız gerekiyor:

Bu durumda güven aralığının güven düzeyinin %95 olmasını istiyoruz yani almamız gereken Z α/2 değeri 1,96 olsun.
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-54dda39d0da5b29f2d25728b89565859_l3.png)
Sorun ifadesi zaten bize örneklem büyüklüğünün n=700 olduğunu ve örneklemde gözlemlenen oranın p=0,40 olduğunu söylüyor, bu nedenle verileri oran için güven aralığı formülüne yerleştiriyoruz ve aralığın sınırlarını hesaplıyoruz:

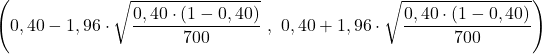
![]()
Sonuç olarak, incelenen popülasyonun oranı %95 güven düzeyiyle %36 ila %44 arasındadır.