Orantı için hipotez testi
Bu makale istatistikte oran hipotez testinin ne olduğunu açıklamaktadır. Bu nedenle orantıya ilişkin hipotez testinin formülünü ve ayrıca bunun nasıl yapıldığını tam olarak anlamak için adım adım bir alıştırma bulacaksınız.
Orantı için hipotez testi nedir?
Oran hipotez testi, bir popülasyon oranına ilişkin sıfır hipotezinin reddedilip reddedilmeyeceğini belirlemek için kullanılan istatistiksel bir yöntemdir.
Dolayısıyla, hipotez test istatistiğinin oran ve anlamlılık düzeyine ilişkin değerine bağlı olarak sıfır hipotezi reddedilir veya kabul edilir.
Hipotez testinin aynı zamanda hipotez karşıtlıkları, hipotez testi veya anlamlılık testi olarak da adlandırılabileceğini unutmayın.
Oran için Hipotez Testi Formülü
Oran için hipotez testi istatistiği, örneklem oranındaki farktan oranın önerilen değerinin çıkarılmasıyla oranın standart sapmasına bölünerek elde edilen değere eşittir.
Bu nedenle oran için test hipotezi formülü şu şekildedir:

Altın:
-

orana ilişkin hipotez testi istatistiğidir.
-

örnek oranıdır.
-

önerilen oranın değeridir.
-

örneklem büyüklüğüdür.
-

oranın standart sapmasıdır.
Oran için hipotez testi istatistiğini hesaplamanın yeterli olmadığını, ancak sonucun yorumlanması gerektiğini unutmayın:
- Oran için hipotez testi iki taraflı ise, istatistiğin mutlak değeri Z α/2 kritik değerinden büyükse sıfır hipotezi reddedilir.
- Oran için hipotez testi sağ kuyrukla eşleşirse, istatistiğin Z α kritik değerinden büyük olması durumunda sıfır hipotezi reddedilir.
- Oran için hipotez testi sol kuyrukla eşleşirse, istatistiğin -Z α kritik değerinden küçük olması durumunda sıfır hipotezi reddedilir.
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7d5bd583532769e3014286e8ffd94c9f_l3.png)
Kritik değerlerin normal dağılım tablosundan kolaylıkla elde edilebileceğini unutmayın.
Oran için Hipotez Testi Örneği
Oran hipotez testinin tanımını ve formülünü gördükten sonra kavramı daha iyi anlamak için bir örnek çözeceğiz.
- Üreticisine göre belirli bir hastalığa karşı ilaç %70 etkilidir. Araştırmacılar oranın farklı olduğuna inandıkları için laboratuvarda bu ilacın etkinliğini test ediyoruz. Bunun için ilaç 1000 hastadan oluşan bir örneklem üzerinde test ediliyor ve 641 kişi iyileşiyor. Araştırmacıların hipotezini reddetmek veya reddetmemek için popülasyon oranı üzerinde %5 anlamlılık düzeyinde bir hipotez testi yapın.
Bu durumda nüfus oranına ilişkin hipotez testinin sıfır hipotezi ve alternatif hipotezi şöyledir:
![Rendered by QuickLaTeX.com \begin{cases}H_0: p=0,70\\[2ex] H_1:p\neq 0,70 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f7da8281eeecc022e2ec7daea6a9756e_l3.png)
Örnekteki ilaçla iyileşenlerin oranı şöyle:
![]()
Yukarıda görülen formülü uygulayarak orana ilişkin hipotez testi istatistiğini hesaplıyoruz:
![Rendered by QuickLaTeX.com \begin{aligned} \displaystyle Z&=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}\\[2ex]Z&=\frac{0,641-0,70}{\displaystyle\sqrt{\frac{0,70\cdot (1-0,70)}{1000}}} \\[2ex] Z&=-4,07\end{aligned}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e689388b0a73e91c1e3d8812c2c4c42a_l3.png)
Öte yandan anlamlılık düzeyi 0,05 olduğundan ve bu iki yönlü bir hipotez testi olduğundan testin kritik değeri 1,96’dır.
![]()
Sonuç olarak test istatistiğinin mutlak değeri kritik değerden büyük olduğundan sıfır hipotezini reddedip alternatif hipotezi kabul ediyoruz.
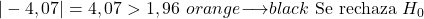 ➤ Bakınız: Ortalama için hipotez testi
➤ Bakınız: Ortalama için hipotez testi
İki örnek oran için hipotez testi
İki numunenin oranlarına yönelik hipotez testi, iki farklı popülasyonun oranlarının eşit olduğunu belirten boş hipotezi reddetmek veya kabul etmek için kullanılır.
Bu nedenle, iki örnekli oranlar için bir hipotez testinin sıfır hipotezi her zaman şöyledir:
![]()
Alternatif hipotez üç seçenekten biri olabilir:
*** QuickLaTeX cannot compile formula:
\begin{array}{l}H_1:p_1\neq p_2\\[2ex]H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio of the two samples is calculated as follows:[latex]p=\cfrac {x_1+x_2}{n_1+n_2}
*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ...H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio
Please use \mathaccent for accents in math mode.
leading text: ...\[2ex]H_1:p_1 The combined ratio of the two
Please use \mathaccent for accents in math mode.
leading text: ...combined of the two samples is calculated
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
İki örnek oran için hipotez testi istatistiğini hesaplama formülü şöyledir:
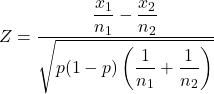
Altın:
-

iki örneklemli oranlar için hipotez test istatistiğidir.
-
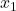
örnek 1’deki sonuçların sayısıdır.
-
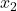
örnek 2’deki sonuçların sayısıdır.
-

örneklem büyüklüğü 1’dir.
-

örneklem büyüklüğü 2’dir.
-

iki numunenin birleşik oranıdır.
k örnek oranı için hipotez testi
K örneğinin oranlarına ilişkin bir hipotez testinde amaç, farklı popülasyonların tüm oranlarının eşit olup olmadığını veya tam tersine farklı oranların olup olmadığını belirlemektir. Dolayısıyla bu durumda sıfır hipotezi ve alternatif hipotez şunlardır:
![Rendered by QuickLaTeX.com \begin{cases}H_0: \text{Todas las proporciones son iguales}\\[2ex] H_1: \text{No todas las proporciones son iguales} \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-77d7e13b427dd927953473a6bfbe9a55_l3.png)
Bu durumda tüm örneklerin birleşik oranı şu şekilde hesaplanır:
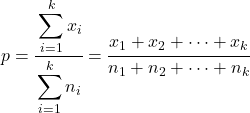
K örnek oranı için hipotez testi istatistiğini bulma formülü şöyledir:
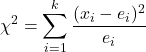
![]()
Altın:
-

k örneklem oranı için hipotez testi istatistiğidir. Bu durumda istatistik ki-kare dağılımını takip eder.
-

örnek i’deki sonuçların sayısıdır.
-

örneklem büyüklüğü i’dir.
-

tüm numunelerin birleşik oranıdır.
-

örnek i’den beklenen isabetlerin sayısıdır. Birleştirilmiş oranın çarpılmasıyla hesaplanır.

örneklem büyüklüğüne göre

.