Oranlardaki fark için güven aralığı
Oranlardaki bir fark için bir güven aralığı (CI), belirli bir güven düzeyine sahip iki nüfus oranı arasındaki gerçek farkı içermesi muhtemel bir değer aralığıdır.
Bu eğitimde aşağıdakiler açıklanmaktadır:
- Bu güven aralığını yaratma motivasyonu.
- Bu güven aralığını oluşturmanın formülü.
- Bu güven aralığının nasıl hesaplanacağına dair bir örnek.
- Bu güven aralığı nasıl yorumlanır?
Oranlardaki fark için CI: motivasyon
Araştırmacılar genellikle iki nüfus oranı arasındaki farkı tahmin etmek isterler. Bu farkı tahmin etmek için her popülasyondan rastgele bir örnek toplayacak ve her örnek için oranı hesaplayacaklar. Daha sonra iki oran arasındaki farkı karşılaştırabilirler.
Ancak örneklem oranları arasındaki farkın popülasyon oranları arasındaki gerçek farka uyup uymadığından emin olamazlar. Bu nedenle iki oran arasındaki fark için bir güven aralığı oluşturabilirler. Bu, nüfus oranları arasındaki gerçek farkı içermesi muhtemel bir değer aralığı sağlar.
Örneğin, A İlçesinde belirli bir yasayı destekleyen sakinlerin oranı ile B İlçesinde yasayı destekleyen sakinlerin oranı arasındaki farkı tahmin etmek istediğimizi varsayalım.
Her ilçede binlerce sakin bulunduğundan, her ilçede her bir sakini araştırmak ve araştırmak çok zaman alıcı ve pahalı olacaktır.
Bunun yerine, her ilçede yaşayanlardan basit rastgele bir örnek alabilir ve iki ilçe arasındaki oranlar arasındaki gerçek farkı tahmin etmek için her örnekte yasanın lehine olan oranı kullanabiliriz:
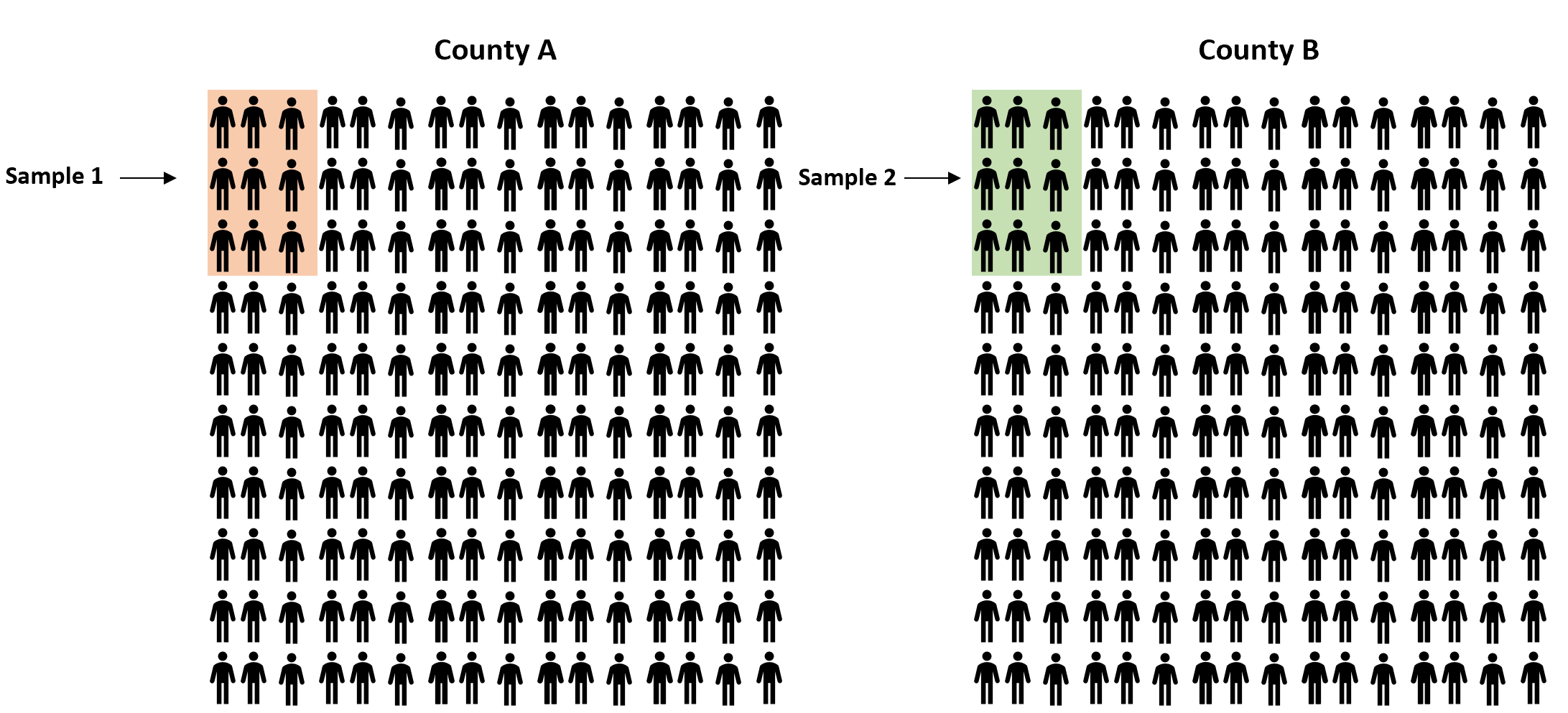
Örneklerimiz rastgele olduğundan, iki örnek arasındaki oran farkının iki popülasyon arasındaki oran farkına tam olarak karşılık geleceği garanti edilmez. Dolayısıyla, bu belirsizliği yakalamak için iki popülasyon arasındaki orantılardaki gerçek farkı içermesi muhtemel bir dizi değer içeren bir güven aralığı oluşturabiliriz.
Oranlardaki fark için CI: formül
İki nüfus oranı arasındaki farka ilişkin güven aralığını hesaplamak için aşağıdaki formülü kullanırız:
Güven aralığı = (p 1 –p 2 ) +/- z*√(p 1 (1-p 1 )/n 1 + p 2 (1-p 2 )/n 2 )
Altın:
- p 1 , p 2 : 1. numunenin oranı, 2. numunenin oranı
- z: güven düzeyine dayalı z-kritik değeri
- n 1 , n 2 : örneklem büyüklüğü 1, örneklem büyüklüğü 2
Kullandığınız z değeri seçtiğiniz güven düzeyine bağlıdır. Aşağıdaki tabloda en yaygın güven düzeyi seçeneklerine karşılık gelen z değeri gösterilmektedir:
| Bir güven düzeyi | z değeri |
|---|---|
| 0,90 | 1.645 |
| 0,95 | 1.96 |
| 0,99 | 2.58 |
Daha yüksek güven düzeylerinin daha büyük z değerlerine karşılık geldiğini ve bunun da daha geniş güven aralıklarına yol açtığını unutmayın. Bu, örneğin aynı veri seti için %95 güven aralığının %90 güven aralığından daha geniş olacağı anlamına gelir.
Oranlardaki fark için CI: örnek
A İlçesinde belirli bir yasayı destekleyen sakinlerin oranı ile B İlçesindeki yasayı destekleyen sakinlerin oranı arasındaki farkı tahmin etmek istediğimizi varsayalım. Her örnek için özet veriler aşağıda verilmiştir:
Örnek 1:
- n1 = 100
- p 1 = 0,62 (yani 100 kişiden 62’si yasayı destekliyor)
Örnek 2:
- n2 = 100
- p 2 = 0,46 (yani 100 kişiden 46’sı yasayı destekliyor)
Nüfus oranlarındaki fark için farklı güven aralıklarını nasıl bulacağınız aşağıda açıklanmıştır:
%90 güven aralığı:
(.62-.46) +/- 1.645*√(.62(1-.62)/100 + .46(1-.46)/100) = [.0456, .2744]
%95 güven aralığı:
(.62-.46) +/- 1.96*√(.62(1-.62)/100 + .46(1-.46)/100) = [.0236, .2964]
%99 güven aralığı:
(0,62-0,46) +/- 2,58*√(0,62(1-0,62)/100 + 0,46(1-0,46)/100) = [-0,0192, 0,3392]
Not: Bu güven aralıklarını Oranlar Farkı Hesaplayıcısı için Güven Aralığı’nı kullanarak da bulabilirsiniz.
Oranlardaki fark için CI : yorumlama
Bir güven aralığını yorumlama şeklimiz şu şekildedir:
[0,0236, 0,2964] güven aralığının iki ilçe arasında yasayı destekleyen sakinlerin oranındaki gerçek farkı içerme olasılığı %95’tir.
Bu aralık “0” değerini içermediğinden, bu, A İlçesinde bu yasayı destekleyen sakinlerin oranında B İlçesine kıyasla gerçek bir fark olduğu anlamına gelir.