Örnek boyut

İle Dr.benjamin anderson Ağustos 3, 2023 İstatistik 0 Yorum

Bu makalede örneklem büyüklüğünün ne olduğu ve istatistikte neden önemli olduğu açıklanmaktadır. Ek olarak, uygun örneklem boyutunun nasıl hesaplanacağını ve çözülmüş bir alıştırmayı keşfederek bunun nasıl yapıldığını görebilirsiniz.

Örneklem büyüklüğü nedir?

Örneklem büyüklüğü (veya örneklem büyüklüğü ), bir çalışmanın örneğini oluşturan bireylerin sayısıdır. İstatistiklerde örneklemin tüm popülasyonu temsil edebilmesi için örneklem büyüklüğü önemlidir.

Bu nedenle istatistiksel bir çalışmanın örneklem büyüklüğünün, evrenin tamamının özelliklerini temsil edecek kadar büyük olması gerekir. Öte yandan, örneklem büyüklüğü aşırı büyük olamaz çünkü araştırma daha pahalı hale gelir. Sonuç olarak örneklem büyüklüğü yeterli olmalı, ne çok büyük ne de çok küçük olmalıdır.

Örneğin bir ülkenin boy uzunluğuna ilişkin bir analiz yapmak istiyorsak, o ülkede yaşayan herkesin boyunu isteyemeyiz çünkü araştırma uzun zaman alır ve çok pahalı olur. Bu nedenle rastgele örnekleme yapılması ve popülasyonun yalnızca temsili bir örneğiyle röportaj yapılması gereklidir.

➤ Bakınız: Örnekleme türleri

Peki uygun örnek boyutunu nasıl bilebiliriz? Bir sonraki bölümde araştırma gereksinimlerine göre uygun örneklem büyüklüğünün nasıl belirleneceğini göreceğiz.

Örneklem büyüklüğü nasıl hesaplanır

Bir ortalamayı tahmin etmek için gerekli numune boyutu, Z _α/2’nin karesinin standart sapma (σ) ile istenen hata marjına (e) bölünmesine eşittir. Bu nedenle örneklem büyüklüğünü hesaplama formülü şu şekildedir:

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

Altın:

$n$

örneklem büyüklüğüdür.
$\alpha$

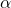
istenilen anlamlılık düzeyidir. Bunu dikkate alarak

$1-\alpha$

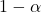
istenilen güven düzeyidir.
$Z_{\alpha/2}$

α/2 olasılığına karşılık gelen standart normal dağılımın niceliğidir. Büyük örneklem büyüklükleri ve %95 güven düzeyi için genellikle 1,96’ya, %99 güven düzeyi için ise genellikle 2,576’ya yakındır.
$\sigma$

standart sapmadır.

Bu formülde popülasyon büyüklüğünün sonsuz olduğu, yani popülasyon büyüklüğünün çok büyük olduğu veya bilinmediği varsayıldığını unutmayın.

Not: Yukarıdaki formül ortalama için güven formülü aralığından türetilmiştir.

Örnek büyüklüğü hesaplama örneği

Bu bölümde örnek olarak istatistiksel bir araştırma için uygun örneklem büyüklüğünü hesaplayacağız.

Bir popülasyonun standart sapmasının 15 civarında olduğunu biliyoruz ancak ortalamasını bilmiyoruz, bu nedenle ortalamayı tahmin etmek için bir çalışma yapmak istiyoruz. %95 güven düzeyinde ±2 hata payı istiyorsak hangi örneklem büyüklüğüne ihtiyacımız var?

Yukarıda gördüğümüz gibi örneklem büyüklüğünü hesaplama formülü şu şekildedir:

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

Bu durumda istenen güven düzeyi %95’tir, dolayısıyla karşılık gelen Z _α/2 değeri 1,96’dır.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

➤ Bakınız: Güven düzeyi değerlerini içeren tablo

Son olarak, artık tüm parametrelerin ne kadar değerli olduğunu bildiğimize göre, değerlerini formülde yerine koyarız ve örneklem büyüklüğünü hesaplarız:

$\begin{aligned}\displaystyle n&=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2\\[2ex] n&=\left(\frac{1,96\cdot 15}{2}\right)^2\\[2ex] n&=216,09 \approx 217 \end{array}$

Kısacası, istenen gereksinimlere sahip popülasyon ortalamasını tahmin etmek için en az 217 kişiden oluşan bir örneğe ihtiyacımız var.

Örneklem büyüklüğü, güven düzeyi ve hata payı

Güven düzeyine ve gerekli hata payına bağlı olarak gerekli örneklem büyüklüğü değişecektir. Dolayısıyla örneklem büyüklüğü, güven düzeyi ve hata payı şu şekilde ilişkilidir:

Örneklem büyüklüğü ve güven düzeyi doğru orantılıdır. Yani güven düzeyi arttıkça örneklem büyüklüğü de artacaktır.
Örneklem büyüklüğü ile hata payı ters orantılıdır. Yani hata payı artarsa örneklem büyüklüğü azalacaktır.
Bu nedenle örneklem büyüklüğünü artırmak güven düzeyini artırabilir veya hata payını azaltabilir.

Diğer numune büyüklüğü formülleri

Tahmin edilecek parametreye bağlı olarak gerekli örneklem büyüklüğü formülü biraz değişir. Bu nedenle bu bölümde bazı özel durumlarda örneklem büyüklüğünün hesaplanmasında faydalı olabilecek diğer formülleri göreceğiz.

bir oranın örneklem büyüklüğü

Bir oranı (p) tahmin etmek için gereken örnek boyutunu hesaplama formülü şöyledir:

$n=\cfrac{N\cdot Z_{\alpha/2}^2\cdot p\cdot (1-p)}{e^2\cdot (N-1)+Z_{\alpha/2}^2\cdot p\cdot (1-p)}$

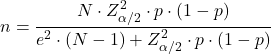
Bir olasılığın örnek büyüklüğü

Bir olasılığı tahmin etmek istediğinizde gerekli örnek boyutunu belirlemek için aşağıdaki formülü kullanmanız önerilir:

$\displaystyle n=\left(\frac{Z_{\alpha/2}}{2\cdot e}\right)^2$

İki bağımsız ortalamayı karşılaştırmak için örneklem büyüklüğü

İki bağımsız ortalamayı belirli bir α riski ve β riskiyle karşılaştırırken örneklem boyutunu hesaplama formülü aşağıdaki gibidir:

$n=\cfrac{2\cdot \sigma^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

Altın

$\Delta$

alternatif hipotezin iki aracı arasındaki farktır.

İki eşleştirilmiş ortalamayı karşılaştırmak için örnek boyutu

Sabit hata α ve hata β ile iki eşleştirilmiş ortalamayı karşılaştırmak istiyorsanız, örnekteki gözlem sayısını bulmak için kullanılacak formül şöyledir:

$n=\cfrac{2\cdot \sigma_d^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

Altın

$\Delta$

alternatif hipotezin iki eşleştirilmiş aracı arasındaki farktır ve

$\sigma_d^2$

Aynı bireyin iki ölçümü arasındaki farkların varyansıdır.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil