Örnekleme dağılımı
Bu makalede istatistikte örnekleme dağılımının ne olduğu ve ne için kullanıldığı açıklanmaktadır. Böylece örnekleme dağılımının anlamını, örnekleme dağılımının somut bir örneğini ve ayrıca en yaygın örnekleme dağılımı türlerine ilişkin formülleri bulacaksınız.
Örnekleme dağılımı nedir?
Örnekleme dağılımı veya örnekleme dağılımı , bir popülasyondaki olası tüm örneklerin dikkate alınmasından kaynaklanan dağılımdır. Başka bir deyişle örnekleme dağılımı, bir evrenden alınabilecek tüm örneklerin örnekleme parametresinin hesaplanmasıyla elde edilen dağılımdır.
Örneğin, istatistiksel bir popülasyondan olası tüm örnekleri çıkarırsak ve her örneğin ortalamasını hesaplarsak, örnek ortalamaları kümesi bir örnekleme dağılımı oluşturur. Daha doğrusu hesaplanan parametre aritmetik ortalama olduğundan ortalamanın örnekleme dağılımıdır.
İstatistikte örnekleme dağılımı, tek bir örnek üzerinde çalışılırken ana kütle parametresinin değerine yaklaşma olasılığını hesaplamak için kullanılır. Benzer şekilde örnekleme dağılımı, belirli bir örneklem büyüklüğü için örnekleme hatasını tahmin etmemizi sağlar.
Örnekleme Dağıtımı Örneği
Artık örnekleme dağılımının tanımını bildiğimize göre, kavramı tam olarak anlamak için basit bir örneğe bakalım.
- Bir kutuya üç top koyuyoruz ve her birinde birden üçe kadar yazılmış bir sayı var, böylece bir topun numarası 1, diğer topun numarası 2 ve son topun numarası da 3 numaradır. n boyutunda bir örnek için = 2, değiştirilen örneklerin seçilmesi durumunda ortalamanın örnekleme dağılımının olasılıklarını hesaplar.
Numuneler değiştirilerek seçilir, yani numunenin ilk elemanını seçmek için alınan top kutuya geri gönderilir ve ikinci ekstraksiyon sırasında tekrar seçilebilir. Bu nedenle popülasyondan alınabilecek tüm örnekler şunlardır:
1,1 1,2 1,3
2,1 2,2 2,3
3,1 3,2 3,3
Böylece olası her örneğin aritmetik ortalamasını hesaplıyoruz:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Bu nedenle popülasyondan rastgele bir örnek seçildiğinde örnek ortalamasının her bir değerinin elde edilme olasılıkları aşağıdaki gibidir:
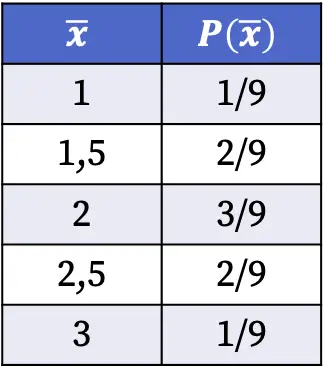
Yukarıdaki tabloda gösterilen örnekleme dağılımının olasılıkları, söz konusu ortalama değere sahip örnek sayısının toplam olası durum sayısına bölünmesiyle hesaplanmıştır. Örneğin: mümkün olan dokuz durumdan ikisinde örneklem ortalaması 1,5’tir, dolayısıyla P(1,5)=2/9.
Örnekleme dağılım türleri
Örnekleme dağılımları (veya örnekleme dağılımları), elde edildikleri örnekleme parametresine göre sınıflandırılabilir. Dolayısıyla, en yaygın dağıtım türleri aşağıdaki gibidir:
- Ortalamanın örnekleme dağılımı : Her örneğin aritmetik ortalamasının hesaplanmasından kaynaklanan örnekleme dağılımıdır.
- Oranlı Örnekleme Dağılımı : Tüm örneklerin oranları hesaplanarak elde edilen örnekleme dağılımıdır.
- Varyans örnekleme dağılımı : Örnekteki tüm varyansların kümesini oluşturan örnekleme dağılımıdır.
- Ortalama örnekleme dağılımının farkı : İki farklı popülasyondan mümkün olan tüm örneklerin ortalamaları arasındaki farkın hesaplanmasından kaynaklanan örnekleme dağılımıdır.
- Oran Farkı Örnekleme Dağılımı : İki anakütleden olası tüm örnekleme oranlarının çıkarılmasıyla elde edilen örnekleme dağılımıdır.
Her bir örnekleme dağılımı türü aşağıda daha ayrıntılı olarak açıklanmaktadır.
Ortalamanın örnekleme dağılımı
Ortalama ile normal bir olasılık dağılımını takip eden bir popülasyon göz önüne alındığında
![]()
ve standart sapma
![]()
ve boyut örnekleri çıkarıldı
![]()
ortalamanın örnekleme dağılımı aşağıdaki özelliklere sahip bir normal dağılımla da tanımlanacaktır:
![Rendered by QuickLaTeX.com \begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-44571aa7337b095ab9c9fa1f746e93a5_l3.png)
Altın
![]()
ortalamanın örnekleme dağılımının ortalamasıdır ve
![]()
onun standart sapmasıdır. Üstelik,
![]()
örnekleme dağılımının standart hatasıdır.
Not: Popülasyon normal bir dağılım izlemiyorsa ancak örneklem büyüklüğü büyükse (n>30), ortalamanın örnekleme dağılımı, merkezi teorem limiti ile yukarıdaki normal dağılıma da yaklaştırılabilir.
Bu nedenle, ortalamanın örnekleme dağılımı normal bir dağılım izlediğinden, örnek ortalamasına ilişkin herhangi bir olasılığı hesaplama formülü şöyledir:

Altın:
-

örnek anlamına gelir.
-

Bu nüfus ortalamasıdır.
-

nüfus standart sapmasıdır.
-

örneklem büyüklüğüdür.
-

standart normal dağılım N(0,1) tarafından tanımlanan bir değişkendir.
Oranın örnekleme dağılımı
Aslında bir örneklemin belli bir kısmını incelediğimizde başarı durumlarını analiz etmiş oluyoruz. Bu nedenle çalışmadaki rastgele değişken binom olasılık dağılımını izlemektedir.
Merkezi limit teoremine göre, büyük boyutlar için (n>30) binom dağılımını normal dağılıma yaklaştırabiliriz. Bu nedenle, oranın örnekleme dağılımı aşağıdaki parametrelerle normal dağılıma yaklaşmaktadır:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f3408076893f390bb65baecfe38e6eff_l3.png)
Altın
![]()
başarı olasılığı ve
![]()
başarısızlık olasılığı
![]()
.
Not: Bir binom dağılımı ancak normal dağılıma yaklaşık olarak şu durumlarda verilebilir:

![]()
Ve
![]()
.
Bu nedenle, oranın örnekleme dağılımı normal bir dağılıma yakınlaştırılabildiğinden, bir numunenin oranına ilişkin herhangi bir olasılığın hesaplanmasına yönelik formül şu şekildedir:

Altın:
-

örnek oranıdır.
-

nüfusa oranıdır.
-

popülasyonun başarısız olma olasılığıdır,

.
-

örneklem büyüklüğüdür.
-

standart normal dağılım N(0,1) tarafından tanımlanan bir değişkendir.
Varyansın Örnekleme Dağılımı
Varyansın örnekleme dağılımı ki-kare olasılık dağılımı ile tanımlanır. Bu nedenle, örnekleme varyans dağılımı istatistiğinin formülü şöyledir:
![]()
Altın:
-

ki-kare dağılımını takip eden varyansın örnekleme dağılımının istatistiğidir.
-

örneklem büyüklüğüdür.
-

örnek varyansıdır.
-

nüfus varyansıdır.
Ortalamalar farkının örnekleme dağılımı
Örneklem büyüklüğü yeterince büyükse (n 1 ≥30 ve n 2 ≥30), ortalama farkın örnekleme dağılımı normal bir dağılım izler. Daha doğrusu söz konusu dağılımın parametreleri şu şekilde hesaplanır:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-90c67b74b4e9326b7869d641a59725d9_l3.png)
Not: Her iki popülasyon da normal dağılıma sahipse, ortalamalardaki farkın örnekleme dağılımı, örneklem büyüklüğünden bağımsız olarak normal bir dağılım izler.
Bu nedenle, ortalamalardaki farkın örnekleme dağılımı normal bir dağılımla tanımlandığından, ortalamalardaki farkın örnekleme dağılımının istatistiğini hesaplamak için formül şu şekildedir:

Altın:
-

örnek i’nin ortalamasıdır.
-

nüfusun ortalamasıdır i.
-

popülasyonun standart sapması i’dir.
-

örneklem büyüklüğü i’dir.
-

standart normal dağılım N(0,1) tarafından tanımlanan bir değişkendir.
Farklı popülasyonlardan alınan numunelerin farklı numune boyutlarına sahip olabileceğini unutmayın.
Oranlardaki farkın örnekleme dağılımı
Orantı örnekleme dağılımındaki fark için seçilen örnekler binom dağılımlarıyla tanımlanır, çünkü pratik amaçlar için oran, başarı durumlarının toplam gözlem sayısına oranıdır.
Ancak merkezi limit teoremi nedeniyle binom dağılımları normal olasılık dağılımlarına yaklaştırılabilir. Bu nedenle oranlardaki farkın örnekleme dağılımı, aşağıdaki özelliklerle normal bir dağılıma yaklaştırılabilir:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a1ce359b5dd6d80f8d27b0b9a1034bed_l3.png)
Not: Oranlardaki farkın örnekleme dağılımı ancak aşağıdaki durumlarda normal dağılıma yaklaşabilir:
![]()
,
![]()
,
![]()
,
![]()
,
![]()
Ve
![]()
.
Bu nedenle, oranlardaki farkın örnekleme dağılımı normal bir dağılıma yakınlaştırılabileceğinden, oranlardaki farkın örnekleme dağılımının istatistiğini hesaplama formülü aşağıdaki gibidir:

Altın:
-

örnek oranı i’dir.
-

i nüfus oranıdır.
-

i popülasyonunun başarısızlık olasılığıdır,

.
-

örneklem büyüklüğü i’dir.
-

standart normal dağılım N(0,1) tarafından tanımlanan bir değişkendir.