Oranın örnekleme dağılımı

İle Dr.benjamin anderson Ağustos 3, 2023 İstatistik 0 Yorum

Bu makalede istatistikte orantı örnekleme dağılımının ne olduğu açıklanmaktadır. Benzer şekilde, orantı örnekleme dağıtım formülünü ve ayrıca adım adım çözülmüş bir alıştırmayı bulacaksınız.

Oranın örnekleme dağılımı nedir?

Oranın örnekleme dağılımı (veya oranların örnekleme dağılımı ), bir popülasyondaki olası her örneğin oranının hesaplanmasından kaynaklanan dağılımdır. Yani, bir evrendeki olası tüm örneklerin örnekleme oranları, oranın örnekleme dağılımını oluşturur.

Başka bir deyişle orantısal örnekleme dağılımı, bir evrenden seçilebilecek tüm örneklerin incelenmesi ve her örneğin örnekleme oranının türetilmesiyle elde edilir. Böylece hesaplanan örneklem oranları kümesi, oranın örnekleme dağılımını oluşturur.

Oranın örnekleme dağılımının ne işe yaradığını merak ediyorsanız istatistiklerde, tek bir örnek analiz edilirken nüfus oranının değerine yaklaşma olasılığını hesaplamak için kullanılır.

➤ Bakınız: Ortalamanın örnekleme dağılımı

Orantılı Örnekleme Dağıtım Formülü

Aslında bir örneklemin belli bir kısmını incelediğimizde başarı durumlarını analiz etmiş oluyoruz. Bu nedenle çalışmadaki rastgele değişken binom olasılık dağılımını izlemektedir.

Merkezi limit teoremine göre, büyük boyutlar için (n>30) binom dağılımını normal dağılıma yaklaştırabiliriz. Bu nedenle, oranın örnekleme dağılımı aşağıdaki parametrelerle normal dağılıma yaklaşmaktadır:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

Altın

$p$

başarı olasılığı ve

$q$

başarısızlık olasılığı

$q=1-p$

Not: Bir binom dağılımı ancak normal dağılıma yaklaşık olarak şu durumlarda verilebilir:

$n>30″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”52″ style=”vertical-align: -2px;”> , <p class=$ $np\ge 5$

$nq\ge 5$

➤ Bakınız: Normal dağılım örnekleri

Bu nedenle, oranın örnekleme dağılımı normal bir dağılıma yakınlaştırılabildiğinden, bir numunenin oranına ilişkin herhangi bir olasılığın hesaplanmasına yönelik formül şu şekildedir:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

Altın:

$\widehat{p}$

örnek oranıdır.
$p$

nüfusa oranıdır.
$q$

popülasyonun başarısız olma olasılığıdır,

$q=1-p$

.
$n$

örneklem büyüklüğüdür.
$Z$

standart normal dağılım N(0,1) tarafından tanımlanan bir değişkendir.

Orantılı Örnekleme Dağıtımının Somut Örneği

Oranlı Örnekleme Dağıtımının tanımını ve ilgili formüllerinin neler olduğunu gördükten sonra, kavramı tam olarak anlamak için aşağıda adım adım çözümlü bir örnek verilmiştir.

Bir sanayi şirketi, parçaları yalnızca %3 hatalı parçayla ürettiğini iddia eden bir fabrikadan partiler halinde parça satın alıyor. Bunu kontrol etmek için şirket 500 parçalık bir siparişi analiz etmeye karar verir. Numunede %5’ten fazla kusurlu parça bulma olasılığı nedir?

Bu durumda, incelemek istediğimiz popülasyonun oranı 0,03’tür, dolayısıyla q parametresi 0,97’ye eşdeğerdir.

$\begin{array}{c}p=0,03\\[2ex]q=1-p=0,97\end{array}$

Dolayısıyla bize sordukları olasılığı bulmak için, önceki bölümde gördüğümüz formülü uygulayarak ilgili istatistiği hesaplamalıyız:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}=\cfrac{0,05-0,03}{\displaystyle\sqrt{\frac{0,03\cdot 0,97}{500}}}=2,62$

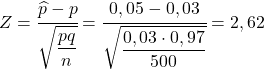
Dolayısıyla %5’ten fazla hatalı parça elde etme olasılığı aşağıdaki olasılığa eşdeğerdir:

$P\left[\widehat{p}>0,05\right]=P[Z>2,62]=1-P[Z\leq 2,62]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”360″ style=”vertical-align: -5px;”> Son olarak <a href=$ Z dağılım tablosunda P[Z≤2.62] olasılığını arıyoruz ve problemin bize sorma olasılığını hesaplıyoruz:

$\begin{array}{l}P\left[\widehat{p}>0,05\right]=\\[2ex]=P[Z>2,62]=\\[2ex]=1-P[Z\leq 2,62]=\\[2ex]=1-0,9956=\\[2ex]=0,0044\end{array}” title=”Rendered by QuickLaTeX.com” height=”167″ width=”162″ style=”vertical-align: 0px;”> Sonuç olarak, analiz edilen numunede %5’ten fazla hatalı parça bulunma olasılığı %0,44’tür. </div>  <div class=$

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Oranın örnekleme dağılımı nedir?

Orantılı Örnekleme Dağıtım Formülü

Orantılı Örnekleme Dağıtımının Somut Örneği

yazar hakkında

Dr.benjamin anderson

Yorum ekle