Orta fark
Bu makalede ortalama sapmanın ne olduğu ve nasıl hesaplandığı açıklanmaktadır. Ayrıca ortalama sapmanın hesaplanmasına ilişkin somut örnekler de bulacaksınız. Üstelik çevrimiçi bir hesap makinesi kullanarak herhangi bir istatistiksel veri setinin ortalama sapmasını hesaplayabileceksiniz.
Ortalama sapma nedir?
Ortalama mutlak sapma olarak da adlandırılan ortalama sapma , istatistiksel dağılımın bir ölçüsüdür.
Bir veri setinin ortalama sapması mutlak sapmaların ortalamasıdır . Bu nedenle ortalama sapma, her veri öğesinin aritmetik ortalamadan sapmalarının toplamının toplam veri öğesi sayısına bölünmesine eşittir.
Başka bir deyişle ortalama sapmanın formülü aşağıdaki gibidir:

👉Herhangi bir veri setinin ortalama sapmasını hesaplamak için aşağıdaki hesaplayıcıyı kullanabilirsiniz.
İstatistikte ortalama sapmaya ortalama mutlak sapma da denir.
Ortalama sapmanın yorumlanması şu şekilde yapılır: ortalama sapmanın değeri ne kadar büyük olursa, bu, verilerin ortalama olarak aritmetik ortalamadan daha uzakta olduğu anlamına gelir; tersine, ortalama sapma ne kadar düşük olursa değer o kadar yakın olur. veriler şöyle. Ortalama sapma bu nedenle bir veri serisinin dağılımını gösterir.
Dağıtıldığı düşünülen diğer önlemler aralık, çeyrekler arası aralık, standart sapma (veya standart sapma), varyans ve varyasyon katsayısıdır.
Ortalama sapma nasıl hesaplanır
Bir veri serisinin ortalama sapmasını hesaplamak için aşağıdaki adımların izlenmesi gerekir:
- İstatistiksel veri setinin aritmetik ortalamasını hesaplayın .
- Her veri noktasının, veriler ile ortalama arasındaki farkın mutlak değeri olarak tanımlanan ortalamadan sapmasını hesaplayın.
- Önceki adımda hesaplanan tüm farkları toplayın.
- Toplam veri sayısına bölün. Elde edilen sonuç, veri serisinin ortalama sapmasıdır.
Özetle ortalama sapmayı bulmak için uygulanması gereken formül şudur:
![]()
Ortalama sapmayı hesaplama örneği
Ortalama sapmanın tanımı göz önüne alındığında, aşağıda bir istatistiksel örneğin ortalama sapmasını hesaplamanın adım adım çözülmüş bir örneği bulunmaktadır. Bu şekilde ortalama sapmanın nasıl elde edileceğini daha iyi anlayacaksınız.
- Bir analist, bir şirketin geçtiğimiz yıldaki ekonomik sonuçlarını inceliyor ve şirketin söz konusu yılın her çeyreğinde elde ettiği kâr hakkında bilgi sahibi oluyor: 2, 3, 7 ve 5 milyon dolar. Verilerin ortalama sapması nedir?
Öncelikle verilerin ortalamasını almamız gerekiyor, bu nedenle toplayıp toplam gözlem sayısına bölüyoruz (4):
![]()
Aritmetik ortalamayı hesapladıktan sonra ortalama sapma formülünü kullanırız:
![]()
Verileri formülde değiştiririz:
![]()
Hesaplamaları payda yapıyoruz:
![]()
![]()
![]()
Son olarak, numunenin ortalama sapmasını elde etmek için toplam veri sayısına bölüyoruz:
![]()
Ortalama Sapma Hesaplayıcı
Ortalama sapmasını hesaplamak için aşağıdaki hesap makinesine bir dizi istatistiksel veri girin. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.
Gruplandırılmış veriler için ortalama sapma
Aralıklara göre gruplandırılmış verilerin ortalama sapmasını hesaplamak için aşağıdaki adımlar izlenmelidir:
- İstatistiksel veri setinin aritmetik ortalamasını belirleyin. Veriler gruplandırıldığı için ortalamayı hesaplamak için kullanılan ifade şu şekildedir:
- Her aralığın, sınıf notu ile ortalama arasındaki farkın mutlak değerine eşdeğer olan ortalamadan sapmasını hesaplayın.
- Her aralığın sapmasını mutlak frekansıyla çarpın.
- Önceki adımdaki tüm sonuçları toplayın ve ardından toplam veri sayısına bölün. Elde edilen sonuç, aralıklarla gruplandırılmış numunenin ortalama sapmasıdır.
![]()
![]()
![]()
![]()
Sonuç olarak, gruplandırılmış verilerden ortalama sapmayı elde etme formülü şöyledir:
![]()
Veriler gruplandırıldığında, bu genellikle çok fazla veri olduğu ve ortalama sapmanın bulunmasının birçok adım içerdiği anlamına gelir. Bu nedenle hesaplamayı gerçekleştirmek için genellikle frekans tabloları kullanılır.
Aşağıda, veriler aralıklar halinde gruplandırıldığında ortalama sapmanın nasıl hesaplanacağına ilişkin adım adım bir alıştırma bulunmaktadır:
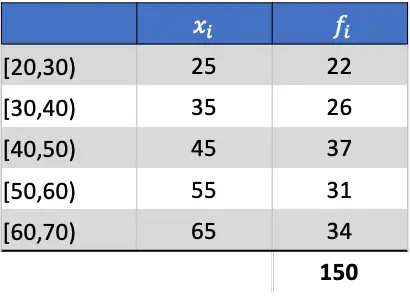
Yapılacak ilk şey, gruplandırılmış verilerin ortalamasını hesaplamaktır. Bunu yapmak için sınıf notunu frekansıyla çarparak tabloya bir sütun ekliyoruz:
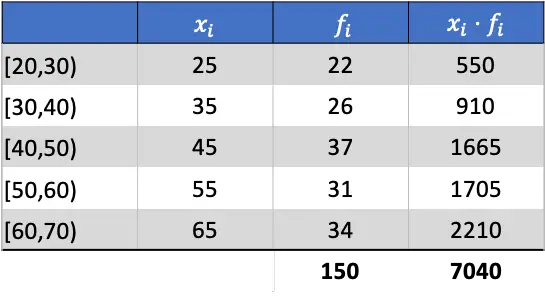
Bu nedenle aritmetik ortalama, eklenen sütunun toplamının mutlak frekansların toplamına bölünmesinin sonucu olacaktır:
![]()
Artık verilerin ortalamasını bildiğimize göre, ortalama sapmayı bulmak için gerekli tüm sütunları ekleyebiliriz:
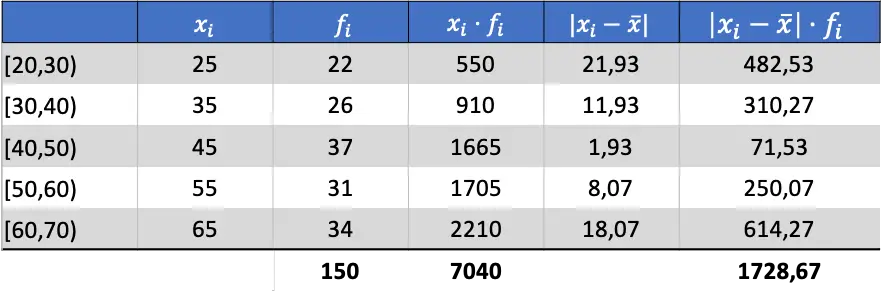
Bu nedenle, ortalama sapmayı elde etmek için son sütunun toplamını toplam gözlem sayısına bölmeniz gerekir:
![]()