Kök kare ortalama

Burada kök ortalama karenin ne olduğunu ve nasıl hesaplandığını açıklıyoruz. Ayrıca ortalamayı kullanmanın avantajlarını ve dezavantajlarını ve adım adım çözülmüş bir alıştırmayı öğreneceksiniz. Son olarak yazının sonunda yer alan hesap makinesi ile herhangi bir veri setinin ortalama karekökünü hesaplayabileceksiniz.

Ortalama kare nedir?

Kök ortalama kare, tanımlayıcı istatistiklerin merkeziliğinin bir ölçüsüdür. Kök ortalama kare, verilerin karelerinin aritmetik ortalamasının kareköküne eşittir.

Kök ortalama kare aynı zamanda kök ortalama kare veya RMS olarak da adlandırılır.

İkinci dereceden ortalamanın formülü bu nedenle aşağıdaki gibidir:

Kare ortalaması özellikle istatistiksel değişken pozitif ve negatif değerler aldığında kullanışlıdır çünkü her bir veri parçasının karesi alındığında tüm değerler pozitif olur. Bu nedenle ortalama kare, işaretinin önemli olmadığı ancak mutlak değerinin önemli olduğu değişkenleri analiz etmek için kullanılır.

Örneğin, ölçüm hatalarını incelemek için ortalama kare kullanılır, çünkü bu durumlarda hatanın pozitif mi yoksa negatif mi olduğuna bakmıyoruz, bunun yerine ölçüm sırasında hatanın büyüklüğünü analiz ediyoruz.

Ayrıca büyük sayıların kareleri küçük sayıların karelerine göre çok daha yüksek değerlere sahip olduğundan ortadaki karede büyük sayılar küçük sayılara göre daha önemlidir.

Kare ortalama, aritmetik ortalama, ağırlıklı ortalama, geometrik ortalama ve harmonik ortalamanın yanı sıra bir tür istatistiksel ortalamadır.

Ortalama Karekökün Avantajları ve Dezavantajları

İkinci dereceden ortalamanın diğer ortalama türlerine göre avantajları ve dezavantajları vardır.

İkinci dereceden ortalamanın temel avantajı , ayrık bir değişkenin ortalama değerine çok iyi bir yaklaşım elde etmenize olanak sağlamasıdır. Öte yandan, kare ortalamanın en büyük dezavantajı , birden fazla işlemin gerçekleştirilmesi gerektiğinden hesaplamasının oldukça karmaşık olmasıdır.

Buna karşılık, ortalama karekök, hata ölçümlerini analiz etmek için çok kullanışlıdır. Her ne kadar bu özellik yanlış bir ölçümün rms sonucunu önemli ölçüde değiştireceğini ima etse de, yüksek değerlere de çok daha fazla önem verilmektedir.

Kök ortalama kare nasıl hesaplanır

Kök ortalama kareyi hesaplamak için aşağıdaki adımlar gerçekleştirilmelidir:

1. Her istatistiksel verinin karesini hesaplayın.
2. Önceki adımda hesaplanan tüm kareleri toplayın.
3. Sonucu örnekteki veri öğesi sayısına bölün.
4. Önceki değerin karekökünü bulun.
5. Elde edilen sonuç istatistiksel numunenin kare ortalamasıdır.

👉Herhangi bir veri setinin ortalama karekökünü hesaplamak için aşağıdaki hesap makinesini kullanabilirsiniz.

Ortalama kare örneği

Kök ortalama kareyi nasıl elde edeceğimizi öğrendikten sonra, örnek olarak bir veri kümesinin ortalama karekökünü belirleyeceğiz.

• Bir üniversitenin laboratuvar dersinde profesör, öğrencilerinden kimyasallarla bir deney yapmalarını ister. Kimyasal deneyin amacı toplamda 3 litrelik bir çözelti elde etmektir. Öğrenci grupları şu verilere ulaştı:

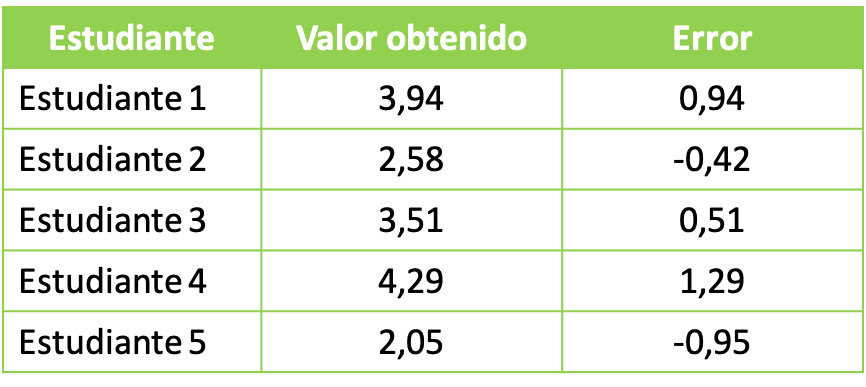
Elde edilen istatistiksel verileri incelemek için, her grubun elde ettiği hatanın kare ortalamasının değerini hesaplamaya devam ediyoruz. Bu nedenle ikinci dereceden ortalama formülünü uyguluyoruz:

Verileri formülde yerine koyarız ve ortalamanın karekökünü hesaplarız:

Böylece deneyde ortalama kareköklere göre elde edilen ortalama hata 0,88 litredir.

Ortalama Kare Hesaplayıcı

Herhangi bir istatistiksel örnekten elde edilen verileri, kök ortalama karesini hesaplamak için aşağıdaki hesap makinesine girin. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.