Ortalama için hipotez testi

İle Dr.benjamin anderson Ağustos 3, 2023 İstatistik 0 Yorum

Bu makale istatistikte ortalamaya ilişkin hipotez testinin ne olduğunu açıklamaktadır. Böylece ortalama için hipotez testi formülünü ve ayrıca adım adım çözülen bir alıştırmayı bulacaksınız.

Ortalama için hipotez testi nedir?

Ortalama için hipotez testi, bir popülasyon ortalamasının sıfır hipotezini reddetmek veya reddetmek için kullanılan istatistiksel bir yöntemdir.

Daha spesifik olarak, ortalama için hipotez testi, test istatistiğinin hesaplanmasını ve sıfır hipotezinin reddedilip reddedilmeyeceğini kritik değerle karşılaştırmayı içerir.

Hipotez testlerinin farklı isimlere sahip olduğunu belirtmek gerekir; istatistiklerde bunlara hipotez karşıtlıkları, hipotez testleri veya anlamlılık testleri de denir.

Ortalama için Hipotez Testi Formülü

Daha sonra ortalama için hipotez testi istatistiğinin nasıl hesaplandığını göreceğiz. Bununla birlikte, varyansın bilinip bilinmemesine bağlı olarak formül biraz değişir, bu nedenle önce varyans bilindiğinde ve sonra varyans bilinmediğinde bunun nasıl yapıldığını göreceğiz.

Bilinen sapma ile

Bilinen varyanslı ortalama için test hipotezi formülü şöyledir:

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle \frac{\sigma}{\sqrt{n}}}$

Altın:

$Z$

ortalama için hipotez testi istatistiğidir.
$\overline{x}$

örnek anlamına gelir.
$\mu$

önerilen ortalama değerdir.
$\sigma$

nüfus standart sapmasıdır.
$n$

örneklem büyüklüğüdür.

Ortalama için hipotez testi istatistiği hesaplandıktan sonra sonuç, sıfır hipotezini reddedecek veya reddedecek şekilde yorumlanmalıdır:

Ortalama için hipotez testi iki taraflı ise, istatistiğin mutlak değeri Z _α/2 kritik değerinden büyükse sıfır hipotezi reddedilir.
Ortalamaya yönelik hipotez testi sağ kuyrukla eşleşiyorsa, istatistiğin Z _α kritik değerinden büyük olması durumunda sıfır hipotezi reddedilir.
Ortalama için hipotez testi sol kuyrukla eşleşirse, istatistik kritik değer -Z _α’dan küçükse sıfır hipotezi reddedilir.

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

Bu durumda kritik değerler standartlaştırılmış normal dağılım tablosundan elde edilir.

Bilinmeyen varyansla

Bilinmeyen varyanslı ortalama için test hipotezi formülü şöyledir:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

Altın:

$t$

Ortalamaya ilişkin hipotez test istatistiğidir ve bu, Öğrenci t dağılımı ile tanımlanır.
$\overline{x}$

örnek anlamına gelir.
$\mu$

önerilen ortalama değerdir.
$s$

örnek standart sapmasıdır.
$n$

örneklem büyüklüğüdür.

Daha önce olduğu gibi, test istatistiğinin hesaplanan sonucu, boş hipotezin reddedilmesi veya reddedilmemesi için kritik değerle yorumlanmalıdır:

Ortalamaya yönelik hipotez testi iki taraflı ise, istatistiğin mutlak değeri _tα/2|n-1 kritik değerinden büyükse sıfır hipotezi reddedilir.
Ortalama için hipotez testi sağ kuyrukla eşleşiyorsa, istatistiğin _tα|n-1 kritik değerinden büyük olması durumunda sıfır hipotezi reddedilir.
Ortalama için hipotez testi sol kuyrukla eşleşirse, istatistik kritik değer -t _α|n-1’den küçükse sıfır hipotezi reddedilir.

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Varyansın bilinmediği durumlarda kritik test değerleri Öğrenci dağılım tablosundan elde edilir.

Ortalama için Gerçek Dünyadan Hipotez Testi Örneği

Nüfus ortalamasına yönelik hipotez testi kavramını tam olarak anlamak için, aşağıda bu tür hipotez testinin gerçek hayattan bir örneğini görebilirsiniz.

Bir teknoloji şirketi sattığı dizüstü bilgisayarın pilinin 6 saat dayandığını iddia ediyor. Bu hipotezin yanlış olup olmadığını, anlamlılık seviyesi α = 0,05 olan bir hipotez testi yaparak kontrol ediyoruz. Bunun için 20 adet satın alınmasına ve her bilgisayarın pil ömrünün gözlemlenmesine karar verilir (değerler saat cinsinden ifade edilmiştir):

5,2 5,9 7,1 4,2 6,5
8,5 4,6 6,8 6,9 5,8
5,1 6,5 7,0 5,3 6,2
5,7 6,6 7,5 5,1 6,1

Bu durumda hipotez testinin ortalamaya ilişkin sıfır ve alternatif hipotezleri şu şekildedir:

$\begin{cases}H_0: \mu=6\\[2ex] H_1:\mu\neq 6 \end{cases}$

Test istatistiğini belirlemek için öncelikle örnek ortalamasını ve örnek standart sapmasını hesaplamamız gerekir:

$\overline{x}=6,13 \qquad s=1,05$

Popülasyon varyansını bilmediğimizden, test istatistiğini elde etmek için bilinmeyen varyanslı ortalamaya yönelik hipotez test formülünü uygulamamız gerekir:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

$\displaystyle t=\frac{6,13-6}{\displaystyle \frac{1,05}{\sqrt{20}}}$

$\displaystyle t=0,68$

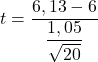
Şimdi hipotez testinin kritik değerini bulmamız gerekiyor, dolayısıyla karşılık gelen değer için Öğrenci t dağılım tablosuna bakıyoruz. Öğrenci t’sinin serbestlik derecesi örneklem büyüklüğünden bir eksiktir (20-1=19) ve buna karşın karşılık gelen olasılık iki yönlü olduğundan anlamlılık düzeyinin yarısı kadardır (0.05/2= 0.025). hipotez testi.

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 19}=2,093\end{array}$

Sonuç olarak, bu iki taraflı bir hipotez testi olduğundan ve test istatistiğinin mutlak değeri kritik değerden küçük olduğundan sıfır hipotezi reddedilmez, alternatif hipotez reddedilir.

$0,68<2,093 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

Ortalamalardaki fark için hipotez testi

Ortalamalar arasındaki fark hipotez testi, iki popülasyonun ortalamalarının aynı olduğunu belirten sıfır hipotezini reddetmek veya kabul etmek için kullanılır.

Dolayısıyla, iki ortalamanın farkına ilişkin bir hipotez testinin sıfır hipotezi her zaman aşağıdaki gibidir:

$H_0: \mu_1=\mu_2$

Alternatif hipotez aşağıdaki üçten biri olabilir:

$\begin{array}{l}H_1:\mu_1\neq \mu_2\\[2ex]H_1:\mu_1>\mu_2\\[2ex]H_1:\mu_1<\mu_2\end{array}$

Daha sonra, varyans bilindiğinde ortalamalar arasındaki farka ilişkin hipotez testi istatistiğini hesaplamak için formül şöyledir:

$\displaystyle Z=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

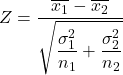
Altın:

$Z$

standart normal dağılıma uyan, bilinen varyansa sahip iki ortalamanın farkı için hipotez test istatistiğidir.
$\overline{x_1}$

örnek 1’in ortalamasıdır.
$\overline{x_2}$

örnek 2’nin ortalamasıdır.
$\sigma_1^2$

popülasyon 1’in varyansıdır.
$\sigma_2^2$

popülasyon 2’nin varyansıdır.
$n_1$

örneklem büyüklüğü 1’dir.
$n_2$

örneklem büyüklüğü 2’dir.

Öte yandan, varyansın bilinmediği durumlarda ortalamalar arasındaki farka ilişkin hipotez testi istatistiğini hesaplama formülü şu şekildedir:

$\displaystyle t=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

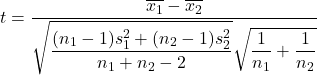
Altın:

$t$

varyansı bilinmeyen iki ortalamanın farkına ilişkin hipotez test istatistiği olup, Öğrenci t dağılımını takip eder.
$\overline{x_1}$

örnek 1’in ortalamasıdır.
$\overline{x_2}$

örnek 2’nin ortalamasıdır.
$s_1^2$

örnek 1’in varyansıdır.
$s_2^2$

örnek 2’nin varyansıdır.
$n_1$

örneklem büyüklüğü 1’dir.
$n_2$

örneklem büyüklüğü 2’dir.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Ortalama için hipotez testi nedir?

Ortalama için Hipotez Testi Formülü

Bilinen sapma ile

Bilinmeyen varyansla

Ortalama için Gerçek Dünyadan Hipotez Testi Örneği

Ortalamalardaki fark için hipotez testi

yazar hakkında

Dr.benjamin anderson

Yorum ekle