Ortalama ve standart sapma arasındaki i̇lişki (örnekle)
Ortalama, bir veri kümesindeki ortalama değeri temsil eder.
Aşağıdaki şekilde hesaplanır:
Örnek ortalama = Σx i / n
Altın:
- Σ: “toplam” anlamına gelen bir sembol
- x i : Bir veri setindeki i’inci gözlem
- n: veri kümesindeki toplam gözlem sayısı
Standart sapma, bir veri setindeki değerlerin ortalamaya göre dağılımını temsil eder.
Aşağıdaki şekilde hesaplanır:
Örneklem standart sapması = √ Σ(x i – x bar ) 2 / (n-1)
Altın:
- Σ: “toplam” anlamına gelen bir sembol
- x i : örneğin i’inci değeri
- x çubuğu : Örnek anlamına gelir
- n: Örneklem büyüklüğü
Ortalama ile standart sapma arasındaki ilişkiye dikkat edin: ortalama, formülde standart sapmayı hesaplamak için kullanılır .
Aslında, numune ortalamasını bilmeden bir numunenin standart sapmasını hesaplayamayız.
Aşağıdaki örnek, pratikte bir veri seti için örnek ortalamanın ve örnek standart sapmanın nasıl hesaplanacağını gösterir.
Örnek: Bir Veri Seti İçin Ortalama ve Standart Sapmanın Hesaplanması
Diyelim ki 10 farklı basketbolcunun attığı sayıları gösteren aşağıdaki veri setine sahibiz:
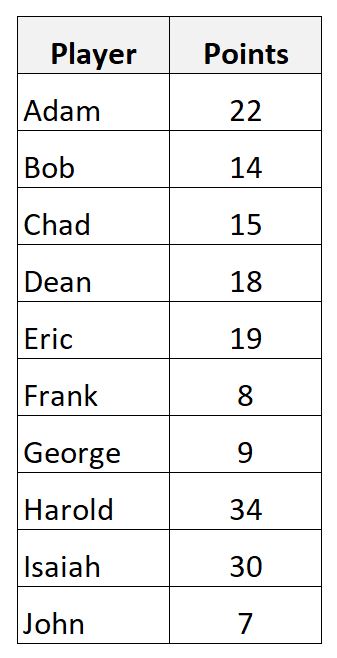Aşağıdaki formülü kullanarak alınan puanların örnek ortalamasını hesaplayabiliriz:
- Örnek ortalama = Σx i / n
- Örneklem ortalaması = (22+14+15+18+19+8+9+34+30+7) / 10
- Örnek ortalama = 17,6
Örneklemde alınan puanların ortalaması 17,6’dır . Bu, tüm oyuncular arasında kazanılan ortalama puan sayısını temsil eder.
Numune ortalamasını öğrendikten sonra numune standart sapmasını hesaplamak için bunu formüle ekleyebiliriz:
- Örneklem standart sapması = √ Σ(x i – x bar ) 2 / (n-1)
- Örneklem standart sapması = √ ((22-17,6) 2 + (14-17,6) 2 + (15-17,6) 2 + (18-17,6) 2 + (19-17,6) 6) 2 + (8-17,6) 2 + (9 -17,6) 2 + (34-17,6) 2 + (30-17,6) 2 + (7-17,6) 2 ) / (10-1)
- Örneklem standart sapması = 9,08
Örneklem standart sapması 9,08’dir . Bu, her bir nokta değeri ile örnek nokta ortalaması arasındaki ortalama mesafeyi temsil eder.
Bir veri kümesinin hem ortalamasını hem de standart sapmasını bilmek faydalıdır çünkü her ölçüm bize farklı bir şey anlatır.
Ortalama bize bir veri kümesinin “merkezi” değerinin nerede olduğuna dair bir fikir verir.
Standart sapma bize bir veri setindeki değerlerin ortalama etrafındaki dağılımı hakkında fikir verir. Standart sapma değeri ne kadar yüksek olursa, değerler bir numunede o kadar dağılmış demektir.
Bu iki değeri bilerek bir veri setindeki değerlerin dağılımı hakkında çok şey öğrenebiliriz.
Ek kaynaklar
Aşağıdaki eğitimler ortalama ve standart sapma hakkında ek bilgi sağlar:
İstatistiklerde ortalama neden önemlidir?
İstatistikte standart sapma neden önemlidir?
Excel’de Ortalama ve Standart Sapma Nasıl Hesaplanır?
yazar hakkında
Dr.benjamin anderson
Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil