Ortalama türler (i̇statistikler)

İle Dr.benjamin anderson Ağustos 6, 2023 İstatistik 0 Yorum

Burada istatistiklerde her türlü ortalamanın ne olduğunu ve nasıl hesaplandığını açıklıyoruz. Her çorap türüne ilişkin formülü ve örnekleri bulacaksınız.

Ancak ortalama türlerinin ne olduğunu görmeden önce mantıksal olarak istatistikte ortalamanın ne olduğunu bilmeliyiz. Bu nedenle devam etmeden önce aşağıdaki bağlantıya başvurmanızı öneririz.

➤ Bakınız: Ortalama (istatistik) nedir?

İstatistikte ortalama türleri nelerdir?

İstatistikte ortalama türleri şunlardır:

Aritmetik ortalama
Ağırlıklı ortalama
Geometrik araçlar
kök kare demektir
harmonik anlamı
genelleştirilmiş ortalama
genelleştirilmiş f-ortalaması
kesilmiş anlamına gelir
çeyrekler arası ortalama
bir fonksiyonun ortalaması

Daha sonra istatistiklerdeki her türlü ortalamanın nasıl hesaplanacağını açıklayacağız. En sık kullanılan beş ortalama türü aritmetik ortalama, ağırlıklı ortalama, geometrik ortalama, ikinci dereceden ortalama ve harmonik ortalamadır. Bu beş ana medya türü hakkında daha fazla ayrıntıya gireceğiz.

Aritmetik ortalama

Aritmetik ortalama, tüm değerlerin toplanması ve ardından toplam veri noktası sayısına bölünmesiyle hesaplanır.

Dolayısıyla aritmetik ortalamanın formülü aşağıdaki gibidir:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+\dots+x_N}{N}$

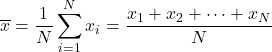
Aritmetik ortalama aynı zamanda aritmetik ortalama olarak da bilinir.

Aritmetik ortalama istatistikte muhtemelen en çok kullanılan ortalama türüdür.

Bu tür ortalamanın nasıl elde edildiğine dair bir örnek görmek için aşağıdaki verilerin aritmetik ortalamasını hesaplayacağız:

$4\quad 7\quad 10\quad 1\quad 8\quad9$

Aritmetik ortalamayı hesaplamak için tüm istatistiksel verileri toplayıp toplam veri sayısına (6) bölmeniz yeterlidir:

$\overline{x}=\cfrac{4+7+10+1+8+9}{6}=6,5$

Ağırlıklı ortalama

Ağırlıklı ortalamayı hesaplamak için, önce her istatistiksel veriyi ağırlığıyla (veya ağırlığıyla) çarpmanız, ardından tüm ürünleri toplamanız ve son olarak ağırlıklı toplamı tüm ağırlıkların toplamına bölmeniz gerekir.

Dolayısıyla ağırlıklı ortalama formülü aşağıdaki gibidir:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+\dots x_N\cdot w_N}{w_1+w_2+\dosts +w_N}$

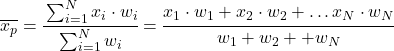
Burada x _i istatistiksel değerdir ve w _i buna karşılık gelen ağırlıktır.

Ağırlıklı ortalamanın anlaşılması daha zor olduğundan, nasıl hesaplandığını adım adım açıklayan aşağıdaki örneğe göz atmanızı öneririz:

➤ Bakınız: Ağırlıklı ortalama örneği

Geometrik araçlar

Bir istatistiksel veri kümesinin geometrik ortalaması, tüm değerlerin çarpımının n’inci köküne eşittir.

Bu tür ortalama, işletme finansmanında getiri oranlarını, ortalama yüzdeleri ve bileşik faizi hesaplamak için kullanılır.

Bu tür depolamanın formülü oldukça karmaşıktır. Aslında tüm istatistiksel kümelerin geometrik ortalaması hesaplanamayabilir ancak bazen bu tür bir ortalama belirlenemeyebilir. Bu nedenle aşağıdaki bağlantıda açıklanan tüm istisnalara başvurmanızı öneririz:

➤ Bakınız: geometrik ortalama formülü

kök kare demektir

Kök ortalama kare, verilerin karelerinin aritmetik ortalamasının kareköküne eşittir.

Ortalama kare formülü bu nedenle aşağıdaki gibidir:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

Bu ortalama türüne aynı zamanda ortalama karekök , ortalama karekök veya RMS de denir.

Kübik ortalamanın da mevcut olduğunu ancak çok özel durumlarda kullanıldığını belirtelim.

Kare ortalamanın avantajları ve dezavantajları vardır; örneğin, istatistiksel değişken pozitif ve negatif değerler aldığında özellikle kullanışlıdır, çünkü her veri parçasının karesi alındığında tüm değerler pozitif olur. Aşağıdaki bağlantıya tıklayarak bu medya türünün daha fazla özelliğini görebilirsiniz:

➤ Bakınız: ortalamanın karekökünün avantajları ve dezavantajları

harmonik anlamı

Harmonik ortalama, toplam istatistiksel veri sayısının her bir değerin karşılıklarının toplamına bölünmesiyle hesaplanır.

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}$

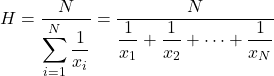
Harmonik ortalama, ortalama hızları, süreleri hesaplamak veya elektronik hesaplamalar yapmak için kullanılır. Bu özellik, harmonik ortalamayı, fiyat ortalamaları veya yüzdelerin hesaplanmasında sıklıkla kullanılan diğer ortalama türlerinden ayırır.

Bu tür ortalamanın hesaplanmasına ilişkin örnekleri aşağıdaki sayfada görebilirsiniz:

➤ Bakınız: harmonik anlam örnekleri

Diğer çorap türleri

Bu bölümde diğer çorap türlerine ait formülleri göreceğiz. Yaygın olarak kullanılmadıkları için her bir tür hakkında detaya girmeyeceğiz ancak başka çorap türlerinin de olduğunu bilmenizde fayda var.

Genelleştirilmiş ortalama, yukarıda görülen ortalama türlerinin bir karışımıdır ve aşağıdaki formül kullanılarak hesaplanır:

$\displaystyle\overline{x}(m) = \left ( \frac{1}{N}\cdot\sum_{i=1}^N{x_i^m} \right ) ^{1/m}$

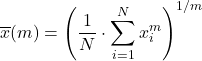
F’nin birebir ve monotonik bir fonksiyon olduğunu kabul edersek genelleştirilmiş f-ortalaması şu şekilde tanımlanır:

$\displaystyle\overline{x} = f^{-1}\left({\frac{1}{N}\cdot\sum_{i=1}^N{f(x_i)}}\right)$

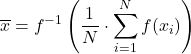
Kırpılmış ortalama, numunenin üst ve alt uçlarındaki gözlemlerin yüzdesinin çıkarılmasından sonra aritmetik ortalamanın hesaplanmasını içerir. Her iki uçta da aynı yüzde reddedilmelidir.

Çeyrekler arası ortalama olarak da adlandırılan çeyrekler arası ortalamayı hesaplamak için, birinci ve dördüncü çeyreklerden gelen veriler ilk önce atılır ve ardından yalnızca numunenin ikinci ve üçüncü çeyreklerinin aritmetik ortalaması hesaplanır. Dolayısıyla bu tür ortalamanın formülü şu şekildedir:

$\displaystyle\overline{x}={2 \over n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}}{x_i}$

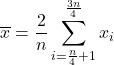
Son olarak bir fonksiyonun ortalamasını da bulabilirsiniz. Kapalı bir aralıkta [a,b] sürekli bir fonksiyonun ortalama değeri aşağıdaki formül kullanılarak hesaplanır:

$\displaystyle\overline{f}=\frac{1}{b-a} \int_a^b f(t) dt$

Örneklem ve popülasyon ortalaması

Son olarak, sıklıkla karıştırılan iki ortalama türü olan örneklem ortalaması ile nüfus ortalaması arasındaki farkın ne olduğunu göreceğiz.

Örnek ortalaması, istatistiksel bir örneğin değerleri üzerinden hesaplanan ortalamadır, yani bir değişkenin tüm değerlerinin bir kısmı üzerinden hesaplanır.

Popülasyon ortalaması, istatistiksel bir popülasyon üzerinden, yani bir değişkenin tüm değerleri üzerinden hesaplanan ortalamadır. Bu nedenle popülasyon ortalaması değişkenin matematiksel beklentisiyle örtüşmektedir.

Yeterince büyük miktarda veri biliniyorsa, örnek ortalamasının popülasyon ortalamasına pratik olarak eşit olduğu düşünülebilir. Ancak gerçekte bir dağılımın tüm değerleri nadiren bilindiğinden popülasyon ortalamasının değerini elde etmek çok zordur.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil