Çoklu standart sapmaların ortalaması nasıl bulunur?

Bazen iki veya daha fazla standart sapmanın ortalamasını bulmak isteyebilirsiniz.

Bunu yapmak için verilerinize bağlı olarak aşağıdaki iki formülden birini kullanabilirsiniz:

Yöntem 1: Eşit örneklem büyüklüğü

K grup arasındaki ortalama standart sapmayı bulmak istiyorsanız ve her grup aynı örneklem büyüklüğüne sahipse aşağıdaki formülü kullanabilirsiniz:

Ortalama SD = √ (s ₁ ² + s ₂ ² + … + s _k ² ) / k

Altın:

• _sk : ^k’inci grubun standart sapması
• k : Toplam grup sayısı

Yöntem 2: Eşit olmayan numune boyutları

K grup arasındaki ortalama standart sapmayı bulmak istiyorsanız ve her grup aynı örneklem büyüklüğüne sahip değilse aşağıdaki formülü kullanabilirsiniz:

Ortalama SD = √ ((n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² + … + (n _k -1)s _k ² ) / (n ₁ +n ₂ + … + n _k – J)

Altın:

• n _k : k ^. grup için örneklem büyüklüğü
• _sk : ^k’inci grubun standart sapması
• k : Toplam grup sayısı

Aşağıdaki örnekler her formülün pratikte nasıl kullanılacağını göstermektedir.

Yöntem 1: Eşit Örneklem Büyüklüğü için Standart Sapmaların Ortalamasının Hesaplanması

Aşağıdaki altı satış dönemi boyunca satışların ortalama standart sapmasını hesaplamak istediğimizi varsayalım:

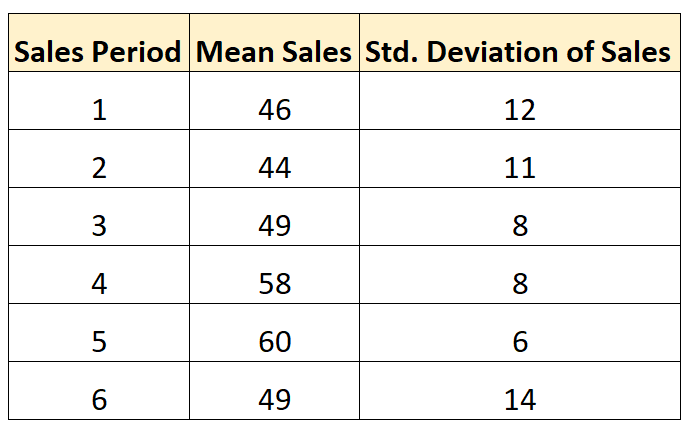
Her satış döneminde aynı sayıda satış işlemi yaptığımızı varsayalım. Dönem başına satışların ortalama standart sapmasını hesaplamak için aşağıdaki formülü kullanabiliriz:

• Ortalama standart sapma = √ (s ₁ ² + s ₂ ² + … + s _k ² ) / k
• Ortalama standart sapma = √ (12 ² + 11 ² + 8 ² + 8 ² + 6 ² + 14 ² ) / 6
• Ortalama standart sapma = 10,21

Dönem başına satışların ortalama standart sapması 10,21’dir .

Yöntem 2: Eşit Olmayan Örneklem Boyutları için Standart Sapmaların Ortalamasını Alma

Aşağıdaki altı satış dönemi boyunca satışların ortalama standart sapmasını hesaplamak istediğimizi varsayalım:

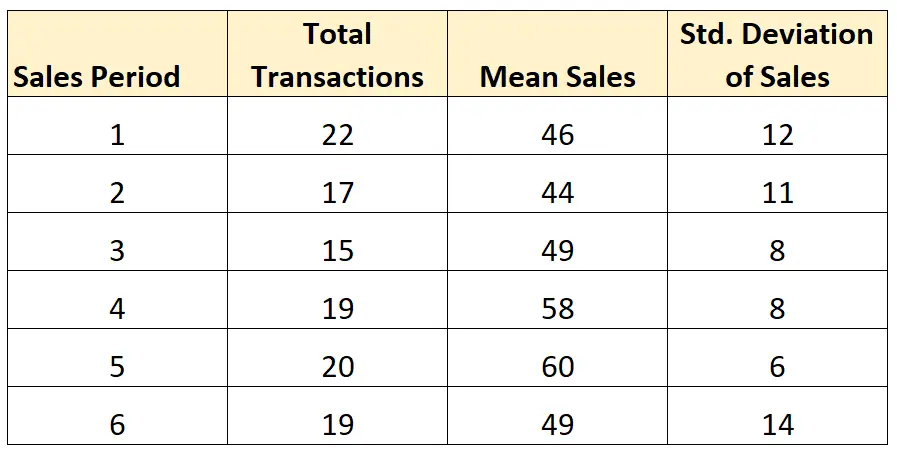
Örneklem büyüklüğü (toplam işlemler) her satış döneminde eşit olmadığından, dönem başına satışların ortalama standart sapmasını hesaplamak için aşağıdaki formülü kullanacağız:

• Ortalama SD = √ ((n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² + … + (n _k -1)s _k ² ) / (n ₁ +n ₂ + … + n _k – J)
• Ortalama SD = √ ((21)12 ² + (16)11 ² + (14)8 ² + (18)8 ² + (19)6 ² + (18)14 ² ) / 106
• Ortalama SD = 10,29

Dönem başına satışların ortalama standart sapması 10,29’dur .

İki örnekteki ortalama standart sapmanın oldukça benzer olduğunu unutmayın. Bunun nedeni, ikinci örnekteki örneklem büyüklüklerinin (toplam işlemlerin) birbirine oldukça yakın olmasıdır.

Ortalama standart sapmayı hesaplamaya yönelik iki yöntem, yalnızca örneklem boyutları gruplar arasında önemli ölçüde farklılık gösterdiğinde önemli ölçüde farklılık gösterir.