Ortalama ve standart sapma verilen bir olasılık nasıl bulunur?

Normal dağılım gösteren bir rastgele değişkenin olasılığını bulmak için aşağıdaki süreci kullanabiliriz.

Adım 1: Z-puanını bulun.

Z-puanı, tek bir veri değerinin ortalamadan ne kadar standart sapma düştüğünü gösterir. Aşağıdaki şekilde hesaplanır:

z-puanı = (x – μ) / σ

Altın:

• x: bireysel veri değeri
• μ: nüfus ortalaması
• σ: popülasyon standart sapması

Adım 2: Z puanına karşılık gelen olasılığı bulun.

Z puanını hesapladıktan sonra buna karşılık gelen olasılığı z tablosunda bulabiliriz.

Aşağıdaki örneklerde bu sürecin farklı senaryolarda nasıl kullanılacağı gösterilmektedir.

Örnek 1: Belirli bir değerin altındaki olasılık

Belirli bir testteki puanlar ortalama μ = 82 ve standart sapma σ = 8 ile normal olarak dağıtılır. Belirli bir öğrencinin testte 84’ten düşük puan alma olasılığı nedir?

Adım 1: Z-puanını bulun.

İlk olarak 84 puanıyla ilişkili z-puanını bulacağız:

z-puanı = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25

Adım 2: Karşılık gelen olasılığı bulmak için z tablosunu kullanın.

Daha sonra z tablosunda 0,25 değerini arayacağız:

Belirli bir öğrencinin 84’ten az puan alma olasılığı yaklaşık %59,87’dir .

Örnek 2: Belirli bir değerden büyük olasılık

Belirli bir penguen türünün boyu, μ = 30 inç ortalaması ve σ = 4 inç standart sapması ile normal olarak dağıtılır. Rastgele bir penguen seçersek boyunun 28 inçten fazla olma olasılığı nedir?

Adım 1: Z-puanını bulun.

İlk olarak 28 inç yüksekliğe ilişkin z-puanını bulacağız.

Puan z = (x – μ) / σ = (28 – 30) / 4 = -2 / 4 = -0,5

Adım 2: Karşılık gelen olasılığı bulmak için z tablosunu kullanın.

Daha sonra -0,5 değerini arayacağız   z tablosunda:

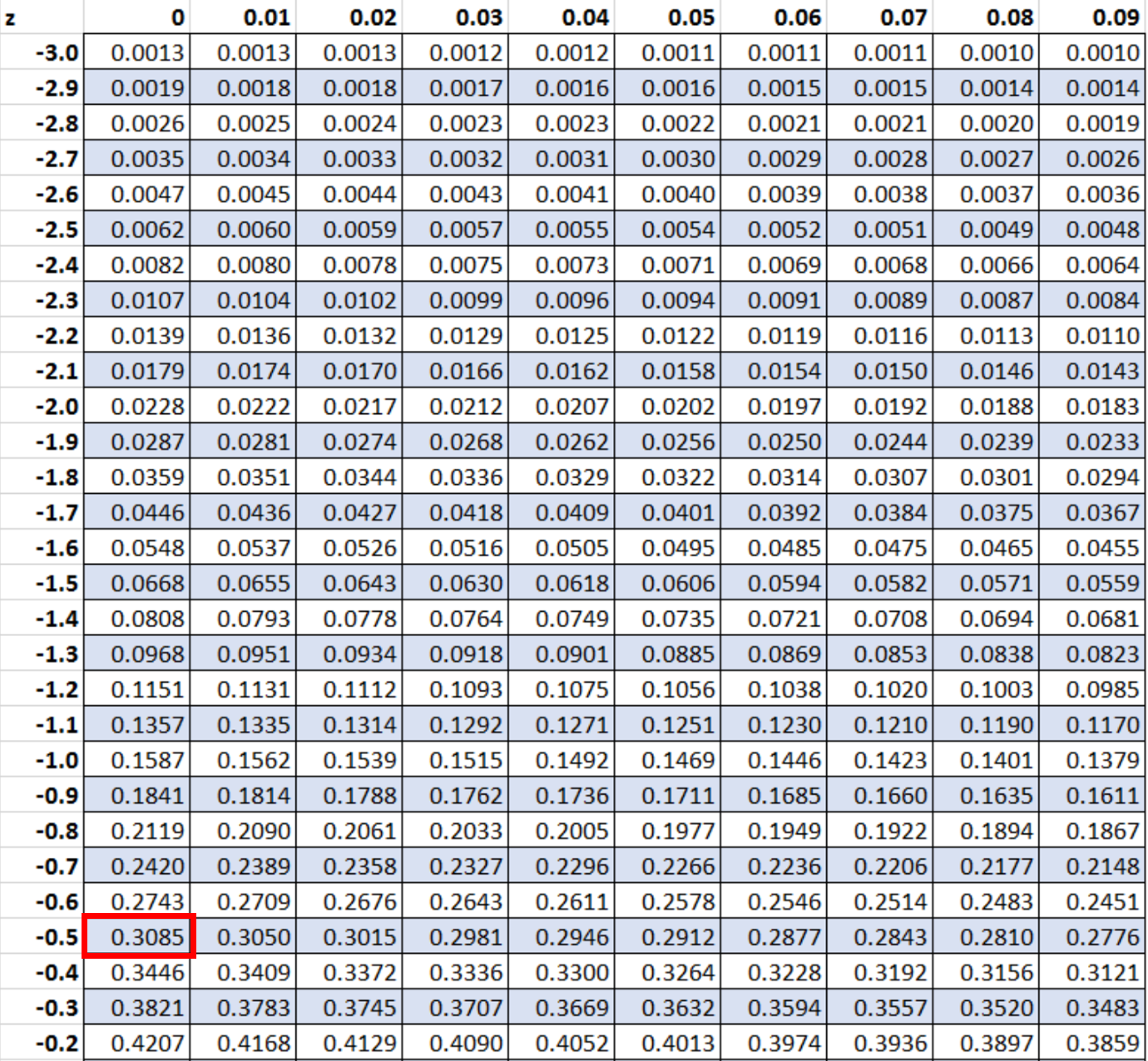
-0,5 z-puanına karşılık gelen değer 0,3085’tir. Bu, bir penguenin 28 inçten kısa olma olasılığını temsil eder.

Ancak bir penguenin 28 inçten uzun olma olasılığını bilmek istediğimiz için bu olasılığı 1’den çıkarmamız gerekiyor.

Yani bir penguenin 28 inçten uzun olma olasılığı: 1 – 0,3085 = 0,6915 .

Örnek 3: İki değer arasındaki olasılık

Belirli bir kaplumbağa türünün ağırlığı, μ = 400 pound ortalaması ve σ = 25 pound standart sapması ile normal olarak dağıtılır. Rastgele bir kaplumbağa seçersek ağırlığının 410 ila 425 pound arasında olma olasılığı nedir?

Adım 1: Z-puanlarını bulun.

İlk olarak 410 kitap ve 425 kitapla ilişkili z puanlarını bulacağız.

410’un z-puanı = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4

425 z puanı = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

Adım 2: Karşılık gelen olasılığı bulmak için z tablosunu kullanın.

İlk önce 0,4 değerini arayacağız.   z tablosunda:

Daha sonra 1 değerini arayacağız   z tablosunda:

Daha sonra küçük değeri büyük değerden çıkaracağız: 0,8413 – 0,6554 = 0,1859 .

Yani rastgele seçilen bir kaplumbağanın 410 pound ile 425 pound arasında ağırlığa sahip olma olasılığı %18,59’dur .

Ek kaynaklar

Z puanından P değeri manuel olarak nasıl hesaplanır?
Z puanları ham puanlara nasıl dönüştürülür?
Belirli bir alanda Z puanları nasıl bulunur?