Ortalamalar arasındaki fark için güven aralığı

Ortalamalar arasındaki fark için bir güven aralığı (CI), belirli bir güven düzeyine sahip iki popülasyon ortalaması arasındaki gerçek farkı içermesi muhtemel bir değer aralığıdır.

Bu eğitimde aşağıdakiler açıklanmaktadır:

• Bu güven aralığını yaratma motivasyonu.
• Bu güven aralığını oluşturmanın formülü.
• Bu güven aralığının nasıl hesaplanacağına dair bir örnek.
• Bu güven aralığı nasıl yorumlanır?

Araçlar arasındaki fark için CI: motivasyon

Araştırmacılar genellikle iki popülasyonun ortalamaları arasındaki farkı tahmin etmek isterler. Bu farkı tahmin etmek için her popülasyondan rastgele bir örnek toplayacak ve her örneğin ortalamasını hesaplayacaklar. Daha sonra iki ortalama arasındaki farkı karşılaştırabilirler.

Ancak örnek ortalamalar arasındaki farkın popülasyon ortalamaları arasındaki gerçek farka karşılık gelip gelmediğinden emin olamazlar. Bu nedenle iki ortalama arasındaki fark için bir güven aralığı oluşturabilirler. Bu, popülasyon ortalamaları arasındaki gerçek farkı içermesi muhtemel bir değer aralığı sağlar.

Örneğin, iki farklı kaplumbağa türü arasındaki ortalama ağırlık farkını tahmin etmek istediğimizi varsayalım. Her popülasyonda binlerce kaplumbağa bulunduğundan, her kaplumbağayı ayrı ayrı tartmak çok zaman alıcı ve pahalı olacaktır.

Bunun yerine, her popülasyondan 15 kaplumbağadan oluşan basit rastgele bir örnek alabilir ve iki popülasyon arasındaki ortalama ağırlıktaki gerçek farkı tahmin etmek için her örneğin ortalama ağırlığını kullanabiliriz:

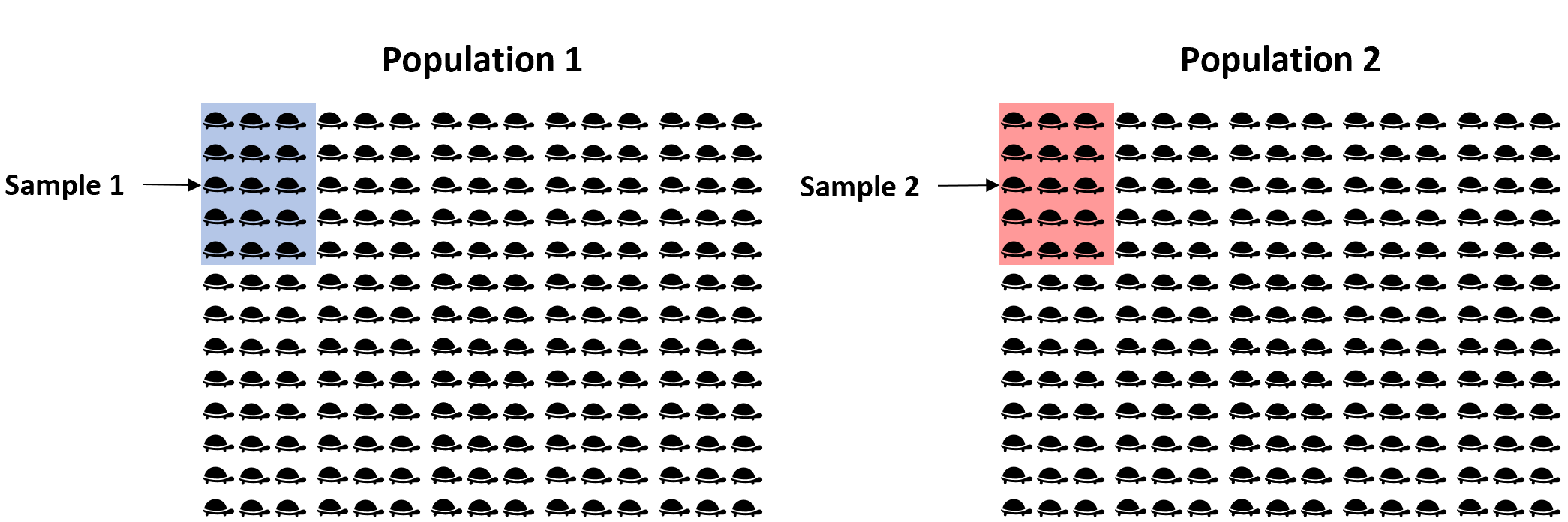
Sorun, örneklerimizin rastgele olmasıdır, bu nedenle iki örnek arasındaki ortalama ağırlık farkının, iki popülasyon arasındaki ortalama ağırlık farkıyla tam olarak eşleşeceği garanti edilmez. Dolayısıyla, bu belirsizliği yakalamak için, iki popülasyon arasındaki ortalama ağırlıktaki gerçek farkı içermesi muhtemel bir dizi değer içeren bir güven aralığı oluşturabiliriz.

Araçlar arasındaki fark için CI: formül

İki ortalama arasındaki farka ilişkin güven aralığını hesaplamak için aşağıdaki formülü kullanırız:

Güven aralığı = ( x ₁ – x ₂ ) +/- t*√((s _p ² /n ₁ ) + (s _p ² /n ₂ ))

Altın:

• x ₁ , x ₂ : örnek 1’in ortalaması, örnek 2’nin ortalaması
• t: güven düzeyine ve (n ₁ + n ₂ -2) serbestlik derecesine dayalı t-kritik değeri
• _sp ² : birleştirilmiş varyans
• n ₁ , n ₂ : örneklem büyüklüğü 1, örneklem büyüklüğü 2

Altın:

• Birleştirilmiş varyans şu şekilde hesaplanır: s _p ² = ((n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² ) / (n ₁ +n ₂ -2)
• T-kritik değeri t, ters t dağılımı hesaplayıcısı kullanılarak bulunabilir.

Araçlar arasındaki fark için CI: örnek

İki farklı kaplumbağa türü arasındaki ortalama ağırlık farkını tahmin etmek istediğimizi varsayalım. Bu nedenle her popülasyondan rastgele 15 kaplumbağa örneği toplayacağız. Her numunenin özet verileri aşağıda verilmiştir:

Örnek 1:

• x1 = ₃₁₀
• ₁ = 18,5
• _n1 = 15

Örnek 2:

• x2 ₌ 300
• _s2 = 16,4
• _n2 = 15

Popülasyon ortalama ağırlıklarındaki gerçek fark için farklı güven aralıklarını nasıl bulacağınız aşağıda açıklanmıştır:

%90 güven aralığı:

(310-300) +/- 1,70*√((305,61/15) + (305,61/15)) = [-0,8589, 20,8589]

%95 güven aralığı:

(310-300) +/- 2,05*√((305,61/15) + (305,61/15)) = [-3,0757, 23,0757]

%99 güven aralığı:

(310-300) +/- 2,76*√((305,61/15) + (305,61/15)) = [-7,6389, 27,6389]

Not: Bu güven aralıklarını Ortalamalar Arasındaki Fark Hesaplayıcısı için İstatistiksel Güven Aralığı’nı kullanarak da bulabilirsiniz.

Güven düzeyi ne kadar yüksek olursa güven aralığının da o kadar geniş olacağını fark edeceksiniz. Bu mantıklı olmalı, çünkü daha geniş aralıkların gerçek nüfus ortalamasını içerme olasılığı daha yüksektir, dolayısıyla aralığın gerçek nüfus ortalamasını içerdiğinden daha “eminiz”.

Araçlar arasındaki fark için CI : yorumlama

Bir güven aralığını yorumlama şeklimiz şu şekildedir:

[-3.0757, 23.0757] güven aralığının iki kaplumbağa popülasyonu arasındaki ortalama ağırlıktaki gerçek farkı içerme olasılığı %95’tir.

Bu aralık “0” değerini içerdiğinden, bu iki popülasyondaki kaplumbağalar arasında ortalama ağırlık farkı olmamasının mümkün olduğu anlamına gelir. Başka bir deyişle, bu iki popülasyondaki kaplumbağalar arasında ortalama ağırlık açısından bir fark olduğunu %95 güvenle söyleyemeyiz.