Ortalamalar farkının örnekleme dağılımı

İle Ağustos 3, 2023 İstatistik 0 Yorum

Bu makalede istatistikte iki ortalama arasındaki farkın örnekleme dağılımının ne olduğu açıklanmaktadır. Ayrıca ortalamalar farkının örnekleme dağılımına ilişkin formülü ve buna ek olarak adım adım çözülmüş bir alıştırmayı da bulacaksınız.

Ortalamalar farkının örnekleme dağılımı nedir?

Ortalamalardaki farkın örnekleme dağılımı, iki farklı popülasyondan olası tüm örneklerin ortalamaları arasındaki farkların hesaplanmasından kaynaklanan dağılımdır.

Yani, ortalamalar arasındaki farkın örnekleme dağılımını elde etmek için, iki çalışma popülasyonundan olası tüm örneklerin seçilmesi gerekir, ardından seçilen her örneğin ortalaması hesaplanır ve son olarak iki popülasyondan hesaplanan tüm ortalamalar arasındaki fark. Böylece tüm bu işlemlerin uygulanmasından sonra elde edilen değerler kümesi, ortalamalar farkının örnekleme dağılımını oluşturur.

ortalamalar farkının örnekleme dağılımı

Ortalama örnekleme dağılımının farkı, iki farklı popülasyondan rastgele seçilen örneklerin ortalamaları arasındaki farkın, popülasyon ortalamalarındaki farka yakın olma olasılığını hesaplamak için kullanılır.

Ortalamalar farkının örnekleme dağılımı için formül

Örneklem büyüklüğü yeterince büyükse (n 1 ≥30 ve n 2 ≥30), ortalamalardaki farkın örnekleme dağılımı normal bir dağılım izler. Daha doğrusu söz konusu dağılımın parametreleri şu şekilde hesaplanır:

\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}

Not: Her iki popülasyon da normal dağılıma sahipse, ortalamalardaki farkın örnekleme dağılımı, örneklem büyüklüğünden bağımsız olarak normal bir dağılım izler.

Bu nedenle, ortalamalardaki farkın örnekleme dağılımı normal bir dağılımla tanımlandığından, ortalamalardaki farkın örnekleme dağılımının istatistiğini hesaplamak için formül şu şekildedir:

Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}

Altın:

  • \overline{x_i}

    örnek i’nin ortalamasıdır.

  • \mu_i

    nüfusun ortalamasıdır i.

  • \sigma_i

    popülasyonun standart sapması i’dir.

  • n_i

    örneklem büyüklüğü i’dir.

  • Z

    standart normal dağılım N(0,1) tarafından tanımlanan bir değişkendir.

Farklı popülasyonlardan alınan numunelerin farklı numune boyutlarına sahip olabileceğini unutmayın.

Ortalamalar farkının örnekleme dağılımının somut örneği

Ortalama örnekleme dağılımının farkının tanımını ve formülünün ne olduğunu gördükten sonra, ortalama örnekleme dağılımının farkı kavramını anlamayı tamamlamak için adım adım bir örnek göreceğiz.

  • İstatistiksel bir çalışmada belirli bir yaşa gelen kız ve erkek çocukların boy farkını analiz etmek istiyoruz. Bu yaştaki erkek nüfusunu tanımlayan dağılımın ortalamasının 157 cm, standart sapmasının 9 cm, buna karşılık bu yaştaki kız nüfusunu tanımlayan dağılımın ortalamasının 148 cm olduğunu biliyoruz. cm ve standart sapması 7 cm’dir. Bu yaştan 30 erkek çocuktan ve bu yaştan 35 kızdan oluşan bir örneklem seçilirse, erkek örnekleminin ortalama boyunun kız örnekleminin ortalama boyundan 12 cm daha büyük olma olasılığı nedir?

Bu sorunu çözmek için yapılacak ilk şey, ortalama örnekleme dağılımı farkının istatistiğini hesaplamaktır. Bu nedenle yukarıda görülen formülü uyguluyoruz:

Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right)}=\cfrac{12-(157-148)}{\displaystyle\sqrt{\frac{9^2}{30}+\frac{7^2}{35}}}=1,48

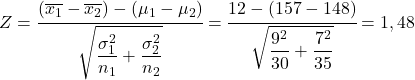
Dolayısıyla erkeklerin ortalama örnek boylarının kızların ortalama boylarından 12 cm daha büyük olma olasılığı, Z değişkeninin 1,48’den büyük olma olasılığına eşdeğerdir.

P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”253″ style=”vertical-align: -5px;”></p> </p> <p> Bu nedenle <a href=Z tablosunda Z>1,48 olasılığını arıyoruz:

P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”331″ style=”vertical-align: -5px;”></p> </p> <p> Kısacası erkek çocukların ortalama boy uzunluğunun kızların ortalama boyundan 12 cm fazla olma olasılığı %6,94’tür.</p> </div><!-- End Content --> <!-- Start Author Box --> <div class=

yazar hakkında

Dr.Benjamin Anderson
Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Yorum ekle

E-posta hesabınız yayımlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir