Ortalamalardaki fark için güven aralığı
Bu makalede istatistiklerde ortalamalar arasındaki farka ilişkin güven aralığının ne olduğu ve ne için kullanıldığı açıklanmaktadır. Böylece, iki ortalamanın farkı için güven aralığını nasıl hesaplayacağınızı ve adım adım çözülen bir alıştırmayı keşfedeceksiniz.
Ortalamalar arasındaki fark için güven aralığı nedir?
Ortalamalar farkı için güven aralığı, iki popülasyonun ortalamaları farkının değerinin belirli bir güven düzeyinde bulunduğu bir maksimum değer ve bir minimum değer sağlayan bir aralıktır.
Örneğin, %95 güven düzeyine sahip iki popülasyonun ortalamaları arasındaki farkın güven aralığı (3,5) ise bu, iki popülasyonun ortalamaları arasındaki farkın 95 olasılıkla 3 ile 5 arasında olacağı anlamına gelir. %.
Bu nedenle istatistiklerde, ortalamalar arasındaki farka ilişkin güven aralığı, iki popülasyon ortalaması arasındaki farkın aralarında bulunduğu iki değeri tahmin etmek için kullanılır. Böylece, iki örnekten elde edilen verileri kullanarak popülasyon ortalamaları arasındaki farkı yaklaşık olarak tahmin etmek mümkündür.
Ortalamalardaki fark için güven aralığı formülü
Ortalamalardaki farka ilişkin güven aralığı formülü, popülasyon varyanslarının bilinip bilinmediğine ve bilinmiyorsa popülasyon varyanslarının eşit olduğunun varsayılıp varsayılamayacağına bağlıdır. . Daha sonra her durumda ortalamalar arasındaki farka ilişkin güven aralığının nasıl hesaplandığını göreceğiz.
bilinen sapmalar
İki popülasyonun varyansları 1-α güven düzeyiyle bilindiğinde ortalamalar arasındaki fark için güven aralığını hesaplamaya yönelik formül aşağıdaki gibidir:
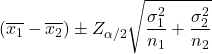
Altın:
-

örnek i’nin ortalamasıdır.
-

popülasyonun standart sapması i’dir.
-

α/2 olasılıkla standart normal dağılımın değeridir.
-

örneklem büyüklüğü i’dir.
Popülasyon varyanslarının değeri genellikle bilinmediğinden bu durum en az görülen durumdur.
bilinmeyen ve eşit varyanslar
İki popülasyonun varyansları bilinmediğinde ancak eşit olduğu tahmin edilebildiğinde, 1-α güven düzeyine sahip ortalamalar farkı için güven aralığını hesaplamaya yönelik formül aşağıdaki gibidir:
![]()
Altın:
-

örnek i’nin ortalamasıdır.
-

havuzlanmış standart sapmadır.
-

α/2 olasılığı ile n 1 + n 2 -2 serbestlik derecesinin Öğrenci t dağılımının değeridir.
-

örneklem büyüklüğü i’dir.
Bu durumda popülasyon varyanslarının eşdeğer olduğu varsayıldığından, aşağıdaki formülle hesaplanan güven aralığını hesaplamak için birleşik standart sapma kullanılır:

Altın
![]()
örnek i’nin standart sapmasıdır.
Bilinmeyen ve farklı varyasyonlar
İki popülasyonun varyansları bilinmediğinde ve eşit olduğu varsayılamazsa, 1-α güven düzeyiyle ortalamalar farkı için güven aralığını hesaplamaya yönelik formül aşağıdaki gibidir:
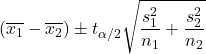
Altın:
-

örnek i’nin ortalamasıdır.
-
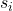
örnek i’nin standart sapmasıdır.
-

α/2 olasılıklı Öğrenci t dağılımının değeridir.
-

örneklem büyüklüğü i’dir.
Bu durumda Öğrenci t dağılımının serbestlik derecesi aşağıdaki formül kullanılarak hesaplanır:

Altın
![]()
örnek i’nin standart sapmasıdır.
Ortalamalardaki fark için güven aralığının somut örneği
Ortalamalar farkı için güven aralığının tanımını ve farklı formüllerin neler olduğunu gördükten sonra, şimdi iki ortalamanın farkı için güven aralığının nasıl hesaplandığını özümsemeyi bitirmek için somut bir örnek göreceğiz.
- Tütünün çocukların doğum ağırlığı üzerindeki etkisini araştırmak istiyoruz. Bunu yapmak için iki örnek karşılaştırılır: ilk örnek, anneleri sigara içmeyen çocuklardan, ikinci örnek ise anneleri sigara içen çocuklardan oluşur (örnek parametreleri aşağıda belirtilmiştir). Ortalamalar arasındaki fark için güven aralığını %95 güven düzeyiyle hesaplayın.
- Sigara içmeyen anneler:
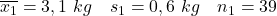
- Sigara içen anneler:
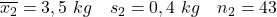
- Sigara içmeyen anneler:
Bu durumda popülasyon varyanslarının değerlerini bilmiyoruz ancak popülasyon varyanslarının eşdeğer olduğunu varsayabiliriz çünkü çok benzer özelliklere sahip iki popülasyonla karşı karşıyayız. Bu nedenle, ortalamalar arasındaki farka ilişkin güven aralığı formülü şu şekildedir:
![]()
Böylece, iki numunenin standart sapmalarından birleşik standart sapmayı hesaplıyoruz:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(39-1)\cdot 0,6^2+(43-1)\cdot 0,4^2}{39+43-2}}\\[2ex]\displaystyle s_p&=0,50\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-688958252e9838e7fddc2ddcb9061b01_l3.png)
Aynı şekilde, Öğrenci t dağılımının olasılık dağılım tablosunda, 80 serbestlik derecesinin Öğrenci t dağılımının değerini %2,5 olasılıkla bulmamız gerekir:
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025|80}=1,990\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5e4ea90fdc33c9a3d3dab0f1d9d29af0_l3.png)
Son olarak, ortalamalar arasındaki fark için verileri güven aralığı formülüne yerleştiririz ve hesaplamaları yaparız:
![]()
![]()
![]()
Dolayısıyla problemin ortalamaları arasındaki farka ilişkin güven aralığı aşağıdaki gibidir:
![]()