İstatistiklerde ortalama neden önemlidir?

Bir veri kümesinin ortalaması , veri kümesinin ortalama değerini temsil eder. Aşağıdaki şekilde hesaplanır:

Ortalama = Σx _i / n

Altın:

• Σ: “toplam” anlamına gelen bir sembol
• x _i : Bir veri setindeki ^i’inci gözlem
• n: veri kümesindeki toplam gözlem sayısı

Örneğin, 11 gözlem içeren aşağıdaki veri setine sahip olduğumuzu varsayalım:

Veri kümesi: 3, 4, 4, 6, 7, 8, 12, 13, 15, 16, 17

Veri setinin ortalaması şu şekilde hesaplanır:

Ortalama = (3+4+4+6+7+8+12+13+15+16+17) / 11 = 9,54

İstatistiklerde ortalama aşağıdaki nedenlerden dolayı önemlidir:

1. Ortalama bize bir veri kümesinin “merkezinin” nerede olduğuna dair bir fikir verir.

2. Hesaplanma şekli nedeniyle ortalama, bir veri setindeki her gözlemden elde edilen bilgileri içerir.

Aşağıdaki örnek bu iki nedeni göstermektedir.

Örnek: Bir veri kümesinin ortalamasını hesaplama

Diyelim ki elimizde belli bir şehirdeki 10.000 farklı evin satış fiyatlarını içeren bir veri setimiz var.

Binlerce satırlık ham veriye bakmak yerine, o şehirdeki evlerin ortalama satış fiyatını hızlı bir şekilde anlamak için ortalama değeri hesaplayabiliriz.

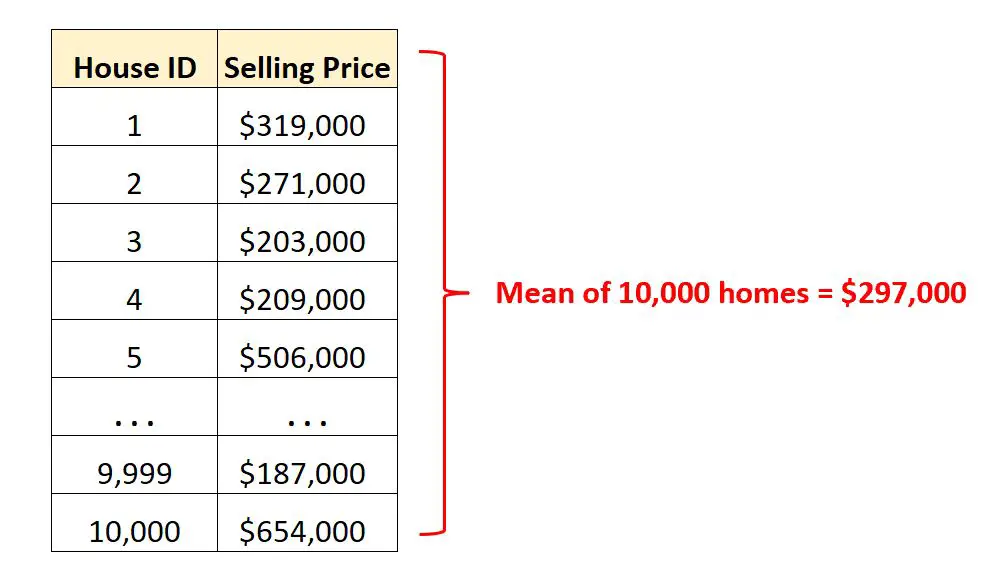
Ortalama satış fiyatının 297.000 dolar olduğunu bilmek bize bu şehirde “tipik” bir evin ne kadara satıldığı konusunda fikir veriyor.

Ortalamanın bu tek değerini yorumlamak, tüm ham veri satırlarına bakmaktan çok daha kolaydır.

Ortalamayı hesaplamak için her ev satış fiyatı kullanıldığından, o şehirdeki tüm evlerin toplam satış fiyatını bulmak için ortalama satış fiyatını toplam ev sayısıyla çarpabiliriz:

• Tüm evlerin toplam satış fiyatı = Ortalama satış fiyatı * Ev sayısı
• Tüm evlerin toplam satış fiyatı = 297.000 $ * 10.000
• Tüm evlerin toplam satış fiyatı = 2.970.000.000$

Bu şehirdeki tüm evlerin toplam satış fiyatının 2,97 milyar dolar olduğunu görüyoruz.

Ortalama ne zaman kullanılır?

Veri setlerini analiz ederken genellikle merkezi değerin nerede olduğunu anlamak isteriz.

İstatistikte bir veri kümesinin merkezini ölçmek için kullandığımız iki ortak ölçüm vardır:

• Ortalama : Bir veri kümesindeki ortalama değer
• Medyan : Bir veri kümesindeki medyan değeri

Ortalama, bir veri kümesinin merkezini ölçmenin en yaygın yoludur, ancak aslında aşağıdaki durumlarda yanıltıcı olabilir:

• Dağıtım asimetrik olduğunda.
• Dağıtım aykırı değerler içerdiğinde.

Bunu açıklamak için aşağıdaki iki örneği inceleyin.

Örnek 1: Çarpık bir dağılımın ortalamasını hesaplamak

Belirli bir şehrin sakinleri için aşağıdaki maaş dağılımını düşünün:

Dağılımın sağ tarafındaki yüksek ücretler, ortalamayı dağılımın merkezinden uzaklaştırır.

Bu nedenle, dağılım sağa çarpık olduğundan medyan, bir sakinin “tipik” maaşını ortalamadan daha iyi yansıtır.

Bu özel örnekte ortalama maaş 47.000 Dolar, ortalama maaş ise 32.000 Dolardır.

Dolayısıyla medyan o şehirdeki tipik maaşı çok daha iyi temsil ediyor.

Örnek 2: Aykırı değerlerin varlığında ortalamanın hesaplanması

Belirli bir caddedeki evlerin metrekaresini gösteren aşağıdaki grafiği düşünün:

Ortalama, birkaç aşırı büyük evden büyük ölçüde etkilenirken, medyan etkilenmemektedir.

Ortancanın o sokaktaki bir evin “tipik” metrekaresini ortalamadan daha iyi yakaladığını görebiliriz çünkü aykırı değerlerden etkilenmez.

Özet

İşte bu makaleden çıkan ana çıkarımların kısa bir özeti:

• Ortalama, bir veri kümesindeki ortalama değeri temsil eder.
• Ortalama önemlidir çünkü bize bir veri setinde merkezi değerin nerede olduğuna dair bir fikir verir.
• Ortalama aynı zamanda önemlidir çünkü bir veri setindeki her gözlemden elde edilen bilgileri içerir.
• Bir veri seti çarpık olduğunda veya aykırı değerler içerdiğinde ortalama yanıltıcı olabilir. Bu senaryolarda medyan, bir veri kümesinin “merkezinin” nerede olduğuna dair daha kesin bir fikir verir.

Ek kaynaklar

Aşağıdaki eğitimler diğer tanımlayıcı istatistikler hakkında ek bilgi sağlar:

Medyan istatistikte neden önemlidir?
İstatistikte standart sapma neden önemlidir?
Ortalama ve medyan ne zaman kullanılmalı?