Pareto dağılımı

İle Ağustos 3, 2023 Olasılık 0 Yorum

Bu makalede istatistikte Pareto dağılımının ne olduğu ve ne için kullanıldığı anlatılmaktadır. Ayrıca Pareto dağılım grafiğini ve bu tür olasılık dağılımının özelliklerini de görebileceksiniz.

Pareto dağılımı nedir?

Pareto dağılımı, istatistikte Pareto ilkesini modellemek için kullanılan sürekli bir olasılık dağılımıdır. Dolayısıyla Pareto dağılımı, gerçekleşme olasılığı diğer değerlerden çok daha yüksek olan birkaç değere sahip bir olasılık dağılımıdır.

80-20 kuralı olarak da adlandırılan Pareto yasasının, bir olgunun nedeninin çoğunun nüfusun küçük bir kısmından kaynaklandığını söyleyen istatistiksel bir ilke olduğunu unutmayın.

Pareto dağılımının iki karakteristik parametresi vardır: ölçek parametresi x m ve şekil parametresi α.

X\sim \text{Pareto}(\alpha,x_m)

Başlangıçta Pareto dağılımı, nüfusun küçük bir kısmından kaynaklandığı için nüfus içindeki servet dağılımını tanımlamak için kullanılıyordu. Ancak şu anda Pareto dağılımının birçok uygulaması vardır; örneğin kalite kontrolde, ekonomide, bilimde, sosyal alanda vb.

Pareto dağılımı, adını dağılımı formüle eden ekonomist Vilfredo Pareto’dan almıştır. Ancak en çok Pareto şemasıyla tanınır.

➤ Bakınız: Pareto şeması nedir?

Pareto dağılım tablosu

Artık Pareto dağılımının tanımını bildiğimize göre, grafiksel olarak temsil edilen çeşitli Pareto dağılım örneklerine bakalım.

Aşağıda Pareto dağılımının yoğunluk fonksiyonunun grafiğinin karakteristik değerlerine bağlı olarak nasıl göründüğünü görebilirsiniz:

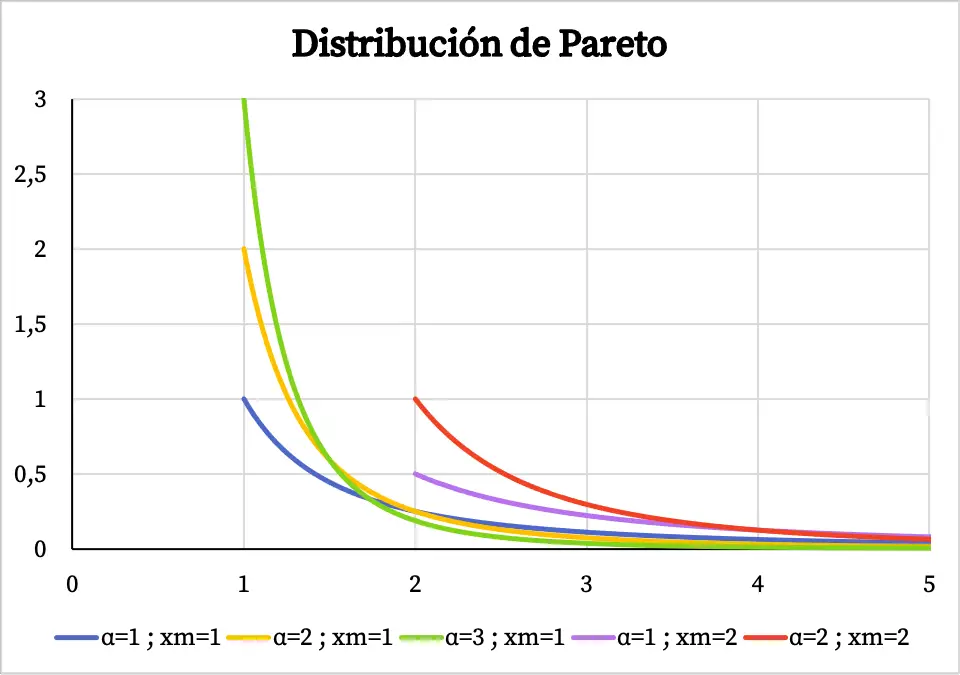
Pareto Dağılım Tablosu

Pareto dağılımının etki alanının x m değerinden +∞’a gittiğine dikkat edin, bu nedenle yoğunluk fonksiyonu x m değerinden önce mevcut değildir.

Öte yandan Pareto dağılımının kümülatif olasılık fonksiyonunun grafiği şu şekildedir:

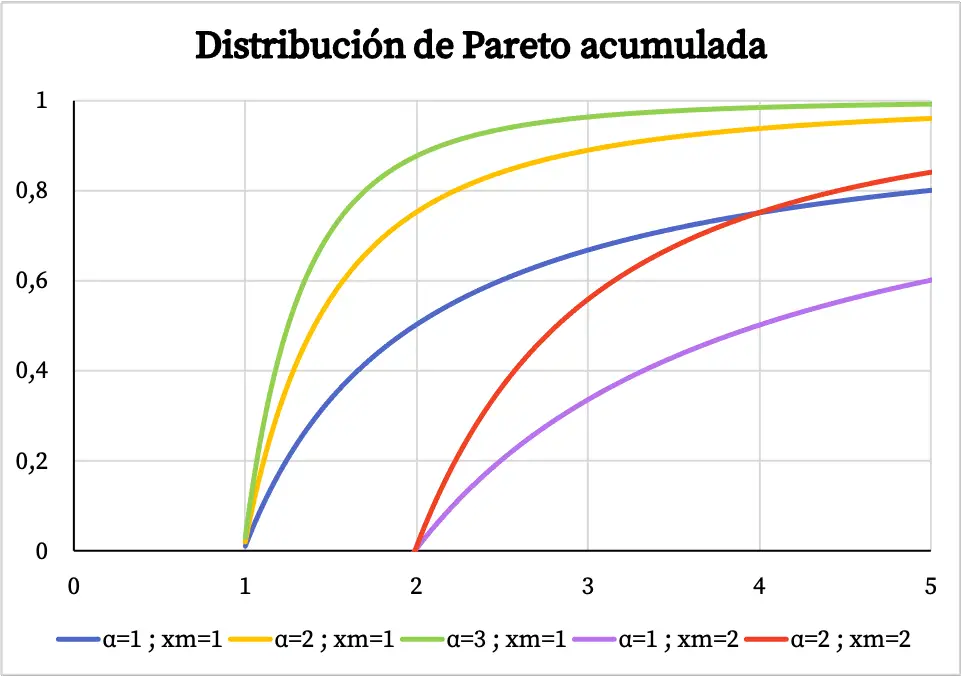
Pareto dağılımının kümülatif olasılığı

Pareto dağılımının özellikleri

Olasılık teorisi ve istatistik ile ilgili Pareto dağılımının en önemli özellikleri aşağıda verilmiştir.

  • Pareto dağılımının eğrisini tanımlayan iki karakteristik parametresi vardır: ölçek parametresi x m ve şekil parametresi α.

X\sim \text{Pareto}(\alpha,x_m)

  • Pareto dağılımının alanı, ölçek parametresinden artı sonsuza kadar tüm gerçek sayılardan oluşur.

x\in [x_m,+\infty)

  • Eğer α 1’den büyükse, Pareto dağılımının ortalaması α çarpı x m ve α eksi 1’in çarpımına eşittir.

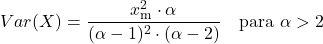
E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”34″ width=”214″ style=”vertical-align: -12px;”></p> </p> <ul> <li> Pareto dağılımının varyansı, dağılımın iki karakteristik parametresine bağlıdır ve aşağıdaki formülle hesaplanır:</li> </ul> <p class=\displaystyle Var(X)=\frac{x_\mathrm{m}^2\cdot \alpha}{(\alpha-1)^2\cdot(\alpha-2)}\quad \text{para }\alpha>2″ title=”Rendered by QuickLaTeX.com” height=”44″ width=”323″ style=”vertical-align: -17px;”></p> </p> <ul> <li> Pareto dağılımının medyanı aşağıdaki ifadeyle belirlenebilir:</li> </ul> <p class=\displaystyle Me=x_\mathrm{m}\cdot \sqrt[\alpha]{2}

  • Pareto dağılımının modu, dağılımın x m ölçek parametresine eşdeğerdir.

Mo=x_m

  • Pareto dağılımının yoğunluk fonksiyonunun formülü şöyledir:

\displaystyle P[X=x]=\frac{\alpha\cdot x_m^\alpha}{x^{\alpha+1}}\quad\text{para }x\geq x_m

  • Benzer şekilde Pareto dağılımının kümülatif olasılık fonksiyonu formülü şöyledir:

\displaystyle P[X\leq x]=1-\left(\frac{x_\mathrm{m}}{x}\right)^\alpha

  • Pareto dağılımının asimetri katsayısı yalnızca şekil parametresi α’ya bağlıdır ve ifadesi şöyledir:

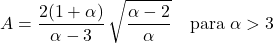
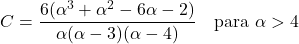
\displaystyle A=\frac{2(1+\alpha)}{\alpha-3}\,\sqrt{\frac{\alpha-2}{\alpha}}\quad\text{para }\alpha>3″ title=”Rendered by QuickLaTeX.com” height=”43″ width=”274″ style=”vertical-align: -14px;”></p> </p> <ul> <li> Pareto dağılımının basıklık katsayısı da α parametresinin değerine bağlı olarak değişir ve aşağıdaki formül kullanılarak hesaplanır:</li> </ul> <p class=\displaystyle C=\frac{6(\alpha^3+\alpha^2-6\alpha-2)}{\alpha(\alpha-3)(\alpha-4)}\quad\text{para }\alpha>4″ title=”Rendered by QuickLaTeX.com” height=”44″ width=”299″ style=”vertical-align: -17px;”></p></p> </div><!-- End Content --> <!-- Start Author Box --> <div class=

yazar hakkında

Dr.Benjamin Anderson
Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Yorum ekle

E-posta hesabınız yayımlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir