Pearson korelasyon katsayısı
Pearson korelasyon katsayısı (“çarpım-moment korelasyon katsayısı” olarak da bilinir) iki değişken X ve Y arasındaki doğrusal ilişkinin bir ölçüsüdür. -1 ile 1 arasında bir değere sahiptir; burada:
- -1, iki değişken arasında tamamen negatif bir doğrusal korelasyonu gösterir
- 0, iki değişken arasında doğrusal bir korelasyon olmadığını gösterir
- 1, iki değişken arasında mükemmel pozitif doğrusal bir korelasyonu gösterir
Pearson korelasyon katsayısını bulma formülü
Bir veri örneği için r ile gösterilen Pearson korelasyon katsayısını bulma formülü ( Wikipedia aracılığıyla ):
Muhtemelen bu formülü hiçbir zaman elle hesaplamak zorunda kalmayacaksınız çünkü bunu sizin yerinize yapacak bir yazılım kullanabilirsiniz, ancak bir örnek üzerinden geçerek bu formülün tam olarak ne işe yaradığını anlamak yararlı olacaktır.
Aşağıdaki veri setine sahip olduğumuzu varsayalım:
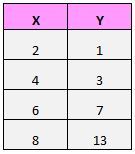
Bu çiftleri (X, Y) bir dağılım grafiğine çizersek, şöyle görünecektir:
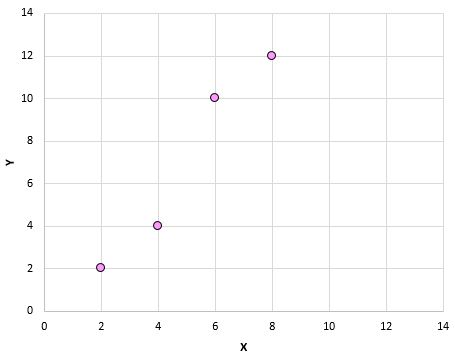
Sadece bu dağılım grafiğine bakarak, X ve Y değişkenleri arasında pozitif bir ilişki olduğunu görebiliriz: X arttıkça Y de artma eğilimindedir. Ancak bu iki değişkenin tam olarak ne kadar pozitif ilişkili olduğunu ölçmek için Pearson korelasyon katsayısını bulmamız gerekiyor.
Formülün payına odaklanalım:
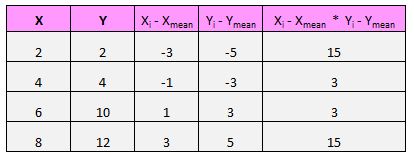
Veri setimizdeki her bir (X, Y) çifti için x değeri ile ortalama x değeri arasındaki farkı, y değeri ile ortalama y değeri arasındaki farkı bulmamız ve daha sonra bu iki sayıyı çarpmamız gerekiyor.
Örneğin ilk çiftimiz (X, Y) (2, 2)’dir. Bu veri setinde x’in ortalama değeri 5 ve y’nin bu veri setinde ortalama değeri 7’dir. Yani bu çiftin x değeri ile x’in ortalama değeri arasındaki fark 2 – 5 = -3 olur. Bu çiftin y değeri ile ortalama y değeri arasındaki fark 2 – 7 = -5’tir. Daha sonra bu iki sayıyı çarptığımızda -3 * -5 = 15 elde ederiz.
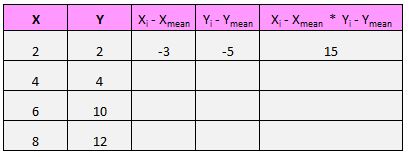
İşte az önce yaptıklarımızın görsel bir özeti:
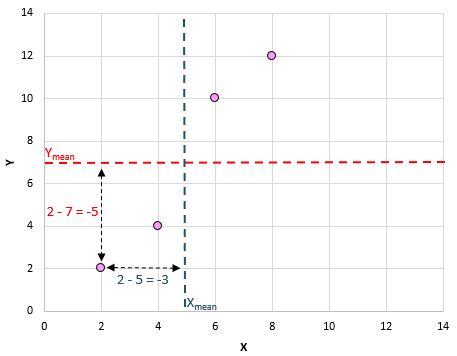
Daha sonra her çift için bunu yapın:
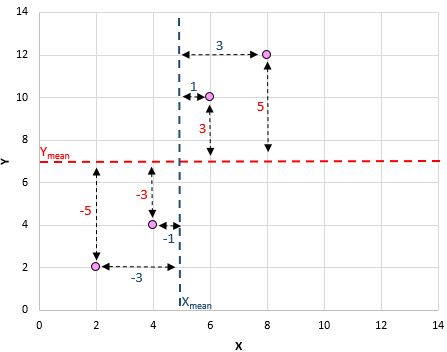
Formülün payını elde etmenin son adımı, tüm bu değerleri bir araya toplamaktır:
15 + 3 +3 + 15 = 36
Daha sonra formülün paydası bize x ve y’nin tüm kare farklarının toplamını bulmamızı, ardından bu iki sayıyı çarpmamızı ve ardından karekök almamızı söyler:
Öncelikle x ve y farklarının karelerinin toplamını bulacağız:
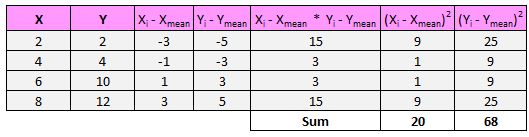
Daha sonra bu iki sayıyı birbiriyle çarpacağız: 20 * 68 = 1.360.
Son olarak karekökünü alacağız: √ 1,360 = 36,88
Böylece formülün payının 36, paydasının ise 36,88 olduğunu bulduk. Bu, Pearson korelasyon katsayımızın r = 36 / 36,88 = 0,976 olduğu anlamına gelir
Bu sayının 1’e yakın olması, X ve Y değişkenlerimiz arasında güçlü bir pozitif doğrusal ilişki olduğunu gösterir. Bu, dağılım grafiğinde gözlemlediğimiz ilişkiyi doğrular.
Korelasyonları görüntüle
Pearson korelasyon katsayısının bize iki değişken arasındaki doğrusal ilişkinin türünü (pozitif, negatif, yok) ve bu ilişkinin gücünü (zayıf, orta, güçlü) söylediğini unutmayın.
İki değişkenin dağılım grafiğini oluşturduğumuzda iki değişken arasındaki gerçek ilişkiyi görebiliriz . Gözlemleyebileceğimiz birçok doğrusal ilişki türü şunlardır:
Güçlü, pozitif ilişki: X eksenindeki değişken arttıkça y eksenindeki değişken de artar. Noktaların yakından kümelenmesi güçlü bir ilişkiyi gösterir. 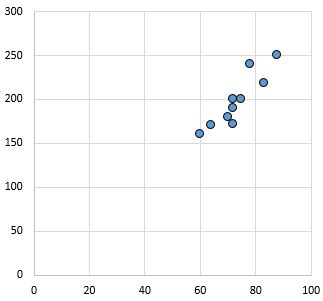
Pearson korelasyon katsayısı: 0,94
Zayıf ve pozitif ilişki: X eksenindeki değişken arttıkça y eksenindeki değişken de artar. Noktaların oldukça dağınık olması zayıf bir ilişkiye işaret etmektedir.
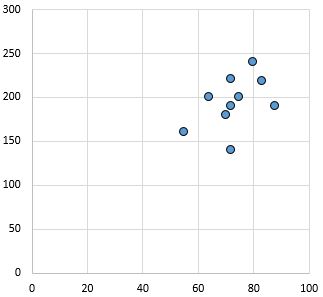
Pearson korelasyon katsayısı: 0,44
İlişki yok: Değişkenler arasında açık (olumlu veya olumsuz) bir ilişki yoktur.
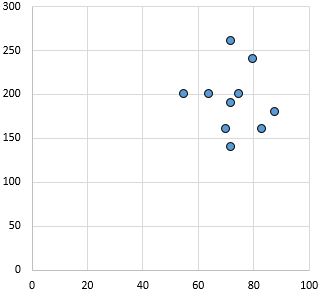
Pearson korelasyon katsayısı: 0,03
Güçlü, negatif ilişki: X eksenindeki değişken arttıkça y eksenindeki değişken azalır. Noktalar sıkı bir şekilde bir araya toplanmıştır, bu da güçlü bir ilişkiyi gösterir.
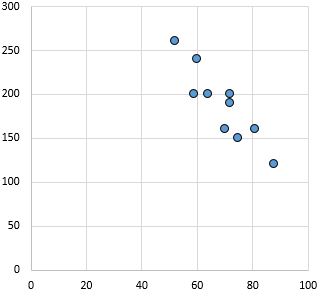
Pearson korelasyon katsayısı: -0,87
Zayıf ve negatif ilişki: X eksenindeki değişken arttıkça y eksenindeki değişken azalır. Noktaların oldukça dağınık olması zayıf bir ilişkiye işaret etmektedir.
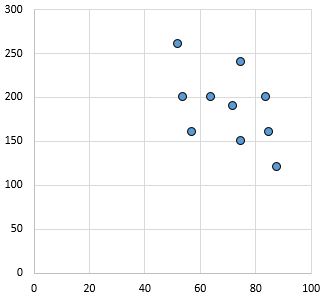
Pearson korelasyon katsayısı: – 0,46
Pearson korelasyon katsayısının öneminin test edilmesi
Bir veri kümesi için Pearson korelasyon katsayısını bulduğumuzda genellikle daha büyük bir popülasyondan alınan bir veri örneğiyle çalışıyoruz. Bu, genel popülasyonda aslında korelasyonsuz olsalar bile iki değişken için sıfırdan farklı bir korelasyon bulmanın mümkün olduğu anlamına gelir.
Örneğin, tüm popülasyondaki her veri noktası için X ve Y değişkenlerine yönelik bir dağılım grafiği oluşturduğumuzu ve bunun şöyle göründüğünü varsayalım:
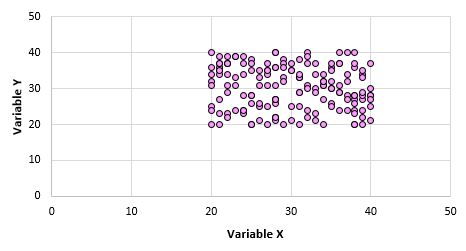
Bu iki değişkenin birbiriyle ilişkili olmadığı açıktır. Ancak evrenden 10 puanlık bir örneklem aldığımızda aşağıdaki noktaları seçmemiz mümkündür:
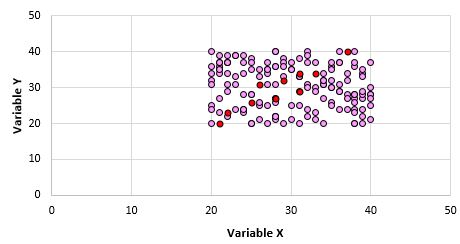
Bu puan örneği için Pearson korelasyon katsayısının 0,93 olduğunu görebiliriz; bu da popülasyon korelasyonu sıfır olmasına rağmen güçlü bir pozitif korelasyona işaret eder.
İki değişken arasındaki ilişkinin istatistiksel olarak anlamlı olup olmadığını test etmek için aşağıdaki test istatistiğini bulabiliriz:
Test istatistiği T = r * √ (n-2) / (1-r 2 )
burada n , örneğimizdeki çiftlerin sayısıdır, r , Pearson korelasyon katsayısıdır ve T testi istatistiği, n-2 serbestlik derecesine sahip bir dağılım izler.
Pearson korelasyon katsayısının öneminin nasıl test edileceğine dair bir örneği inceleyelim.
Örnek
Aşağıdaki veri seti 12 kişinin boy ve kilosunu göstermektedir:

Aşağıdaki dağılım grafiği bu iki değişkenin değerini göstermektedir:

Bu iki değişken için Pearson korelasyon katsayısı r = 0,836’dır.
Test istatistiği T = 0,836 * √ (12 -2) / (1-0,836 2 ) = 4,804.
T dağılımı hesaplayıcımıza göre, 10 serbestlik derecesine sahip 4,804 puanının p değeri 0,0007’dir. 0,0007 < 0,05 olduğundan, bu örnekte ağırlık ve boy arasındaki korelasyonun alfa = 0,05’te istatistiksel olarak anlamlı olduğu sonucuna varabiliriz.
Önlemler
Pearson korelasyon katsayısı bize iki değişkenin doğrusal bir ilişkiye sahip olup olmadığını söylemede yararlı olsa da, Pearson korelasyon katsayısını yorumlarken üç şeyi aklımızda tutmamız gerekir:
1. Korelasyon nedensellik anlamına gelmez. İki değişkenin birbiriyle ilişkili olması, birinin zorunlu olarak diğerinin daha fazla veya daha az sıklıkta ortaya çıkmasına neden olması değildir. Bunun klasik bir örneği, dondurma satışları ile köpekbalığı saldırıları arasındaki pozitif korelasyondur. Yılın belirli zamanlarında dondurma satışları arttığında köpekbalığı saldırıları da artma eğilimindedir.
Bu, dondurma yemenin köpekbalığı saldırılarına neden olduğu anlamına mı geliyor? Tabii ki değil! Bu basitçe yaz aylarında buz tüketiminin ve köpekbalığı saldırılarının artma eğiliminde olduğu anlamına gelir, çünkü buz yazın daha popülerdir ve yaz aylarında daha fazla insan okyanusa gider.
2. Korelasyonlar aykırı değerlere duyarlıdır. Aşırı uç değerler Pearson korelasyon katsayısını önemli ölçüde değiştirebilir. Aşağıdaki örneği düşünün:

X ve Y değişkenlerinin Pearson korelasyon katsayısı 0,00’dır . Ancak veri kümesinde bir aykırı değerin olduğunu hayal edin:

Ancak bu iki değişkene ilişkin Pearson korelasyon katsayısı 0,878’dir . Bu aykırı durum her şeyi değiştirir. Bu nedenle, iki değişken için korelasyon hesaplanırken aykırı değerleri kontrol etmek için değişkenleri bir dağılım grafiği kullanarak görselleştirmek iyi bir fikirdir.
3. Pearson korelasyon katsayısı iki değişken arasındaki doğrusal olmayan ilişkileri yansıtmaz. Aşağıdaki ilişkiye sahip iki değişkenimiz olduğunu varsayalım:

Bu iki değişkenin Pearson korelasyon katsayısı 0,00’dır çünkü doğrusal bir ilişki yoktur. Ancak bu iki değişkenin doğrusal olmayan bir ilişkisi vardır: y değerleri basitçe x değerlerinin karesidir.
Pearson korelasyon katsayısını kullanırken, yalnızca iki değişkenin doğrusal olarak ilişkili olup olmadığını test ettiğinizi unutmayın. Pearson korelasyon katsayısı bize iki değişkenin ilişkili olmadığını söylese bile, yine de bir tür doğrusal olmayan ilişkiye sahip olabilirler. Bu, iki değişken arasındaki ilişkiyi analiz ederken bir dağılım grafiği oluşturmanın yararlı olmasının bir başka nedenidir: doğrusal olmayan bir ilişkiyi tespit etmenize yardımcı olabilir.