İstatistikte olasılık kütle fonksiyonu (pmf) nedir?

Genellikle PMF olarak kısaltılan bir olasılık kütle fonksiyonu , bize ayrı bir rastgele değişkenin belirli bir değeri alma olasılığını söyler.

Örneğin bir zarı bir kez attığımızı varsayalım. Zarın geldiği sayıyı x olarak kabul edersek, x’in farklı değerlere eşit olma olasılığı şu şekilde açıklanabilir:

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

Zarların 1 ile 6 arasında herhangi bir sayıya gelme şansı eşittir.

Bu olasılıkları olasılık kütle fonksiyonu olarak şu şekilde yazabiliriz:

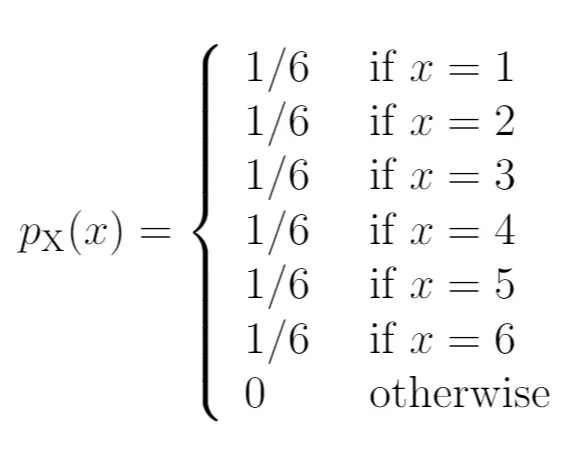
Diyagramın sol tarafı, sağ taraftaki sonuçlarla ilişkili olasılığı gösterir:

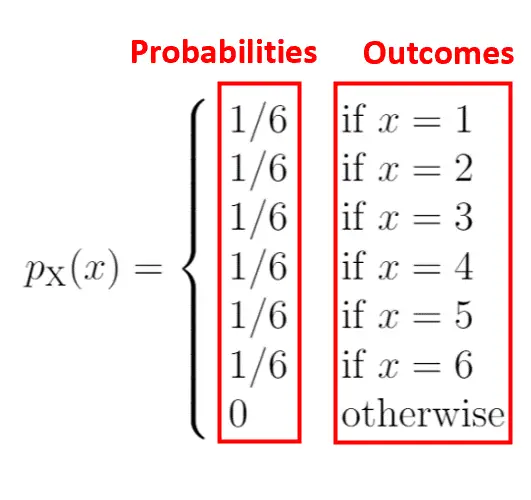
Olasılık kütle fonksiyonunun bir özelliği, tüm olasılıkların toplamının 1 olması gerektiğidir. Bu PMF’nin bu koşulu karşıladığını fark edeceksiniz:

Olasılıkların toplamı = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

Olasılık kütle fonksiyonu desteği, ayrık rastgele değişkenin alabileceği değerler kümesini ifade eder. Bu örnekte zarın değeri bu değerlerden herhangi birini alabileceği için destek {1, 2, 3, 4, 5, 6} olacaktır.

Desteğin dışında PMF değeri sıfırdır. Örneğin zarın “0” veya “7” veya “8” üzerine gelme olasılığı bu sayıların hiçbiri parantez içinde yer almadığı için sıfırdır.

Pratikte olasılık kütle fonksiyonları

Pratikte olasılık kütle fonksiyonlarının en yaygın iki örneği binom dağılımı ve Poisson dağılımı ile ilgilidir.

Binom dağılımı

Eğer bir X rastgele değişkeni binom dağılımını takip ediyorsa, X = k başarısının olasılığı aşağıdaki formülle bulunabilir:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Altın:

• n: deneme sayısı
• k: başarı sayısı
• p: belirli bir denemede başarı olasılığı
• _n C _k : n denemede k başarı elde etmenin yollarının sayısı

Örnek: Bir parayı 3 kez attığımızı varsayalım. Bu 3 atışta 0, 1, 2 ve 3 tura gelme olasılığını belirlemek için yukarıdaki formülü kullanabiliriz:

• P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125
• P(X=1) = ₃ C ₁ * 0,5 ¹ * (1-0,5) ^3-1 = 1 * 1 * (0,5) ² = 0,375
• P(X=2) = ₃ C ₂ * 0,5 ² * (1-0,5) ^3-2 = 1 * 1 * (0,5) ¹ = 0,375
• P(X=3) = ₃ C ₃ * 0,5 ³ * (1-0,5) ^3-3 = 1 * 1 * (0,5) ⁰ = 0,125

Balık dağıtımı

Bir X rastgele değişkeni bir Poisson dağılımını takip ediyorsa, X = k başarısının olasılığı aşağıdaki formülle bulunabilir:

P(X=k) = λ ^k * e ^{– λ} / k!

Altın:

• λ: belirli bir aralıkta meydana gelen ortalama başarı sayısı
• k: başarı sayısı
• e: yaklaşık 2,71828’e eşit bir sabit

Örneğin, belirli bir hastanede saatte ortalama 2 doğum gerçekleştiğini varsayalım. 0, 1, 2, 3 doğum vb. yaşanma olasılığını belirlemek için yukarıdaki formülü kullanabiliriz. belirli bir saatte:

• P(X=0) = 2 ⁰ * e ^{– 2/0} ! = 0,1353
• P(X=1) = 2 ¹ * e ^{– 2/1} ! = 0,2707
• P(X=2) = 2 ² * e ^{– 2/2} ! = 0,2707
• P(X=3) = 2 ³ * e ^{– 2/3} ! = 0,1805

PMF’yi görüntüle

Olasılık kütle fonksiyonlarını sıklıkla çubuk grafiklerle görselleştiririz.

Örneğin, aşağıdaki çubuk grafik, önceki örnekte açıklanan Poisson dağılımı için saat başına doğum sayısıyla ilişkili olasılıkları göstermektedir:

Doğum sayısının sonsuza kadar uzayabileceğini, ancak 10’dan sonra olasılıkların o kadar azaldığını ve bunları çubuk grafikte bile göremeyeceğinizi unutmayın.

PMF’nin özellikleri

Bir olasılık kütle fonksiyonu aşağıdaki özelliklere sahiptir:

1. Destekte tüm olasılıklar pozitiftir. Örneğin bir zarın 1 ile 6 arasına düşme olasılığı pozitif iken diğer tüm sonuçların olasılığı sıfırdır.

2. Tüm sonuçların olasılığı 0 ile 1 arasındadır. Örneğin, zarın 1 ile 6 arasına düşme olasılığı her sonuç için 1/6 veya 0,1666666’dır.

3. Tüm olasılıkların toplamı 1 olmalıdır. Örneğin bir zarın belirli bir sayıya düşme olasılıklarının toplamı 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1’dir. /6 = 1.

Ek kaynaklar

Rastgele değişkenler nelerdir?
CDF veya PDF: fark nedir?
Binom dağılımına giriş
Poisson dağılımına giriş