Poisson güven aralığı nasıl hesaplanır (adım adım)

Poisson dağılımı, olayların bağımsız olarak ve sabit bir ortalama hızla meydana geldiği bilindiğinde, sabit bir zaman aralığında meydana gelen belirli sayıda olayın olasılığını modellemek için kullanılan bir olasılık dağılımıdır.

Bir Poisson sürecinin ortalama oluşum sayısını bilmek yararlı olsa da, ortalama oluşum sayısı etrafında bir güven aralığına sahip olmak daha da yararlı olabilir.

Örneğin rastgele bir günde bir çağrı merkezinde veri topladığımızı ve saat başına ortalama çağrı sayısının 15 olduğunu görelim.

Yalnızca tek bir güne ait verileri topladığımız için çağrı merkezinin yıl boyunca saatte ortalama 15 çağrı aldığından emin olamıyoruz.

Ancak saat başına ortalama çağrı sayısına ilişkin güven aralığını hesaplamak için aşağıdaki formülü kullanabiliriz:

Poisson güven aralığı formülü

Güven aralığı = [0,5*X ² _{2N, α/2} , 0,5*X ² _{2(N+1), 1-α/2} ]

Altın:

• X ² : Ki karenin kritik değeri
• N: Gözlemlenen olayların sayısı
• α: anlamlılık düzeyi

Aşağıdaki adım adım örnek, pratikte %95 Poisson güven aralığının nasıl hesaplanacağını göstermektedir.

1. Adım: gözlemlenen olayları sayın

Bir çağrı merkezinde saat başına ortalama çağrı sayısını 15 olarak hesapladığımızı varsayalım. Yani N = 15 .

Ve %95’lik bir güven aralığı hesapladığımız için aşağıdaki hesaplamalarda α = 0,05’i kullanacağız.

Adım 2: Güven aralığının alt sınırını bulun

Güven aralığının alt sınırı şu şekilde hesaplanır:

• Alt sınır = 0,5*X ² _{2N, α/2}
• Alt sınır = 0,5*X ² _{2(15), 0,975}
• Alt sınır = 0,5*X ² _{30, 0,975}
• Alt sınır = 0,5*16,791
• Alt sınır = 8,40

Not: X ² _{30, 0,975’i} hesaplamak için ki-kare kritik değer hesaplayıcısını kullandık.

3. Adım: Güven aralığının üst sınırını bulun

Güven aralığının üst sınırı şu şekilde hesaplanır:

• Üst sınır = 0,5*X ² _{2(N+1), 1-α/2}
• Üst sınır = 0,5*X ² _{2(15+1), 0,025}
• Üst sınır = 0,5*X ² _{32, 0,025}
• Üst sınır = 0,5*49,48
• Üst sınır = 24,74

Not: X ² _32.0.025’i hesaplamak için ki-kare kritik değer hesaplayıcısını kullandık.

Adım 4: Güven Aralığını Bulun

Daha önce hesaplanan alt ve üst limitleri kullanarak %95 Poisson güven aralığımız şu şekilde ortaya çıkıyor:

• %95 GA = [8,40, 24,74]

Bu, çağrı merkezinin saat başına aldığı gerçek ortalama çağrı sayısının 8,40 çağrı ile 24,74 çağrı arasında olduğundan %95 emin olduğumuz anlamına geliyor.

Bonus: Balık Güven Aralığı Hesaplayıcısı

Poisson güven aralığını otomatik olarak hesaplamak için bu Poisson güven aralığı hesaplayıcısını kullanmaktan çekinmeyin.

Örneğin, az önce manuel olarak hesapladığımız Poisson güven aralığını bulmak için bu hesap makinesini nasıl kullanacağınız aşağıda açıklanmıştır:

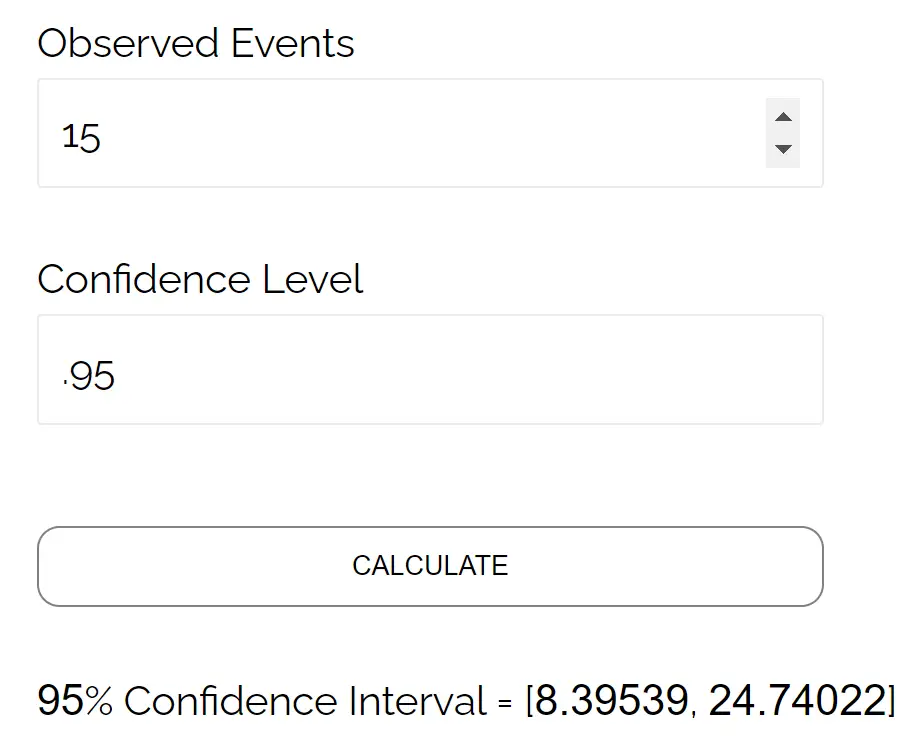
Sonuçların manuel olarak hesapladığımız güven aralığına karşılık geldiğini unutmayın.