Python'da polinom regresyonu nasıl gerçekleştirilir

Regresyon analizi, bir veya daha fazla açıklayıcı değişken ile bir yanıt değişkeni arasındaki ilişkiyi ölçmek için kullanılır.

En yaygın regresyon analizi türü, bir yordayıcı değişken ile bir yanıt değişkeninin doğrusal bir ilişkiye sahip olduğu durumlarda kullanılanbasit doğrusal regresyondur .

Ancak bazen yordayıcı değişken ile yanıt değişkeni arasındaki ilişki doğrusal değildir.

Örneğin, gerçek ilişki ikinci dereceden olabilir:

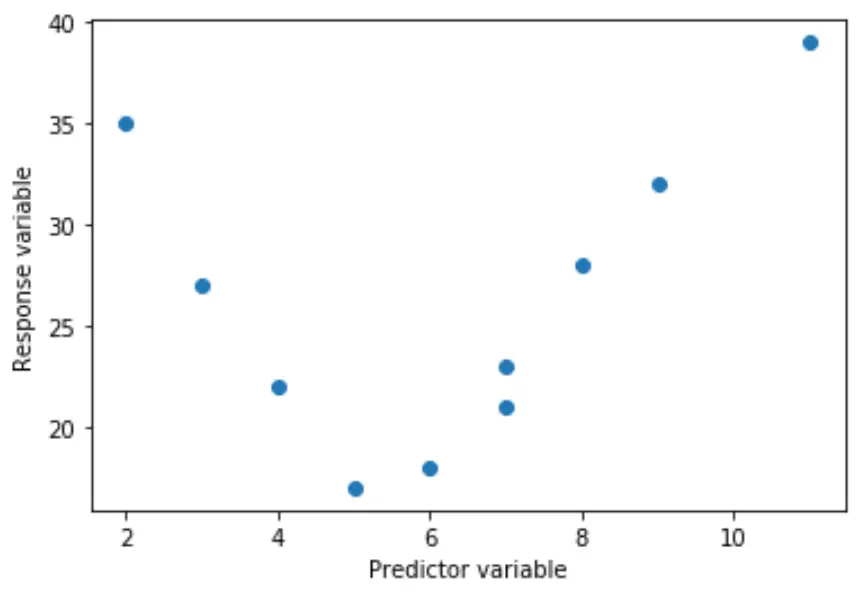
Veya kübik olabilir:

Bu durumlarda değişkenler arasındaki doğrusal olmayan ilişkiyi açıklayabilen polinom regresyonunu kullanmak mantıklıdır.

Bu eğitimde Python’da polinom regresyonunun nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: Python’da Polinom Regresyon

Python’da aşağıdaki tahmin değişkenine (x) ve yanıt değişkenine (y) sahip olduğumuzu varsayalım:

 x = [2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12]
y = [18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]

Bu verilerin basit bir dağılım grafiğini oluşturursak, x ile y arasındaki ilişkinin açıkça doğrusal olmadığını görebiliriz:

 import matplotlib.pyplot as plt

#create scatterplot 
plt.scatter(x, y)

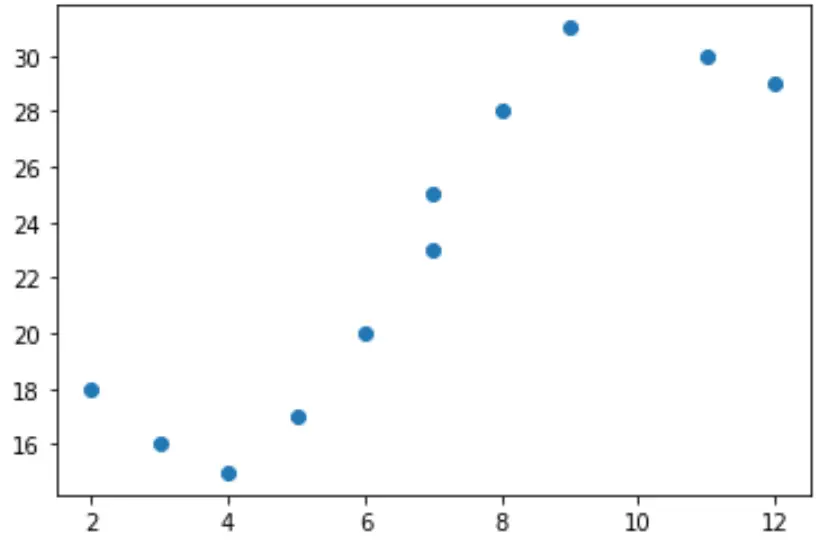
Dolayısıyla bu verilere doğrusal bir regresyon modeli uydurmak mantıklı olmayacaktır. Bunun yerine numpy.polyfit() işlevini kullanarak derece 3’e sahip bir polinom regresyon modeli uydurmaya çalışabiliriz:

 import numpy as np

#polynomial fit with degree = 3
model = np.poly1d(np.polyfit(x, y, 3))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 12, 50)
plt.scatter(x, y)
plt.plot(polyline, model(polyline))
plt.show() 

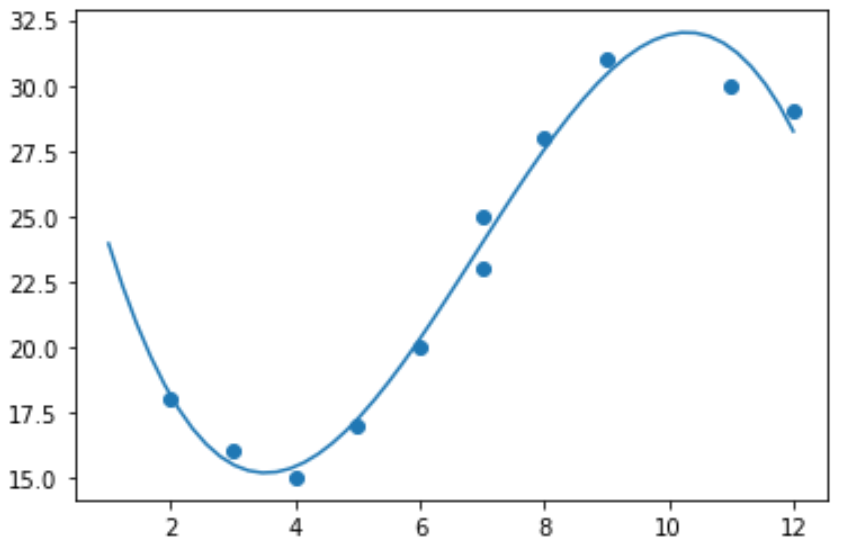
Uygun polinom regresyon denklemini model katsayılarını yazdırarak elde edebiliriz:

 print(model)

poly1d([ -0.10889554, 2.25592957, -11.83877127, 33.62640038])

Uygun polinom regresyon denklemi şöyledir:

y = ^-0,109×3 + ^2,256×2 – 11,839x + 33,626

Bu denklem, açıklayıcı değişkenin belirli bir değeri verildiğinde yanıt değişkeninin beklenen değerini bulmak için kullanılabilir.

Örneğin, x = 4 olduğunu varsayalım. Yanıt değişkeni y için beklenen değer şöyle olacaktır:

y = -0,109(4) ³ + 2,256(4) ² – 11,839(4) + 33,626= 15,39 .

Ayrıca, yordayıcı değişkenler tarafından açıklanabilen yanıt değişkenindeki varyansın oranı olan modelin R-karesini elde etmek için kısa bir fonksiyon da yazabiliriz.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = numpy.polyfit(x, y, degree)
    p = numpy.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = numpy.sum(y)/len(y)
    ssreg = numpy.sum((yhat-ybar)**2)
    sstot = numpy.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(x, y, 3)

{'r_squared': 0.9841113454245183}

Bu örnekte modelin R karesi 0,9841’dir .

Bu, yanıt değişkenindeki değişimin %98,41’inin yordayıcı değişkenler tarafından açıklanabileceği anlamına gelmektedir.