Polinom regresyon

İle Dr.benjamin anderson Ağustos 2, 2023 İstatistik 0 Yorum

Bu makalede istatistikte polinom regresyonunun ne olduğu ve nasıl yapıldığı anlatılmaktadır. Ek olarak polinom regresyonunun gerçekleştirildiği bir örneği görebileceksiniz.

Polinom regresyon nedir?

Polinom regresyon veya polinom regresyon , bağımsız değişken X ile bağımlı değişken Y arasındaki ilişkinin bir polinom kullanılarak modellendiği bir regresyon modelidir.

Örneğin, ikinci dereceden bir polinom regresyon modelinin denklemi y=β ₀ +β ₁ x+β ₂ x ² +ε’dir.

Polinom regresyonu, grafikleri polinom eğrileri olan veri kümelerinin uydurulması için kullanışlıdır. Dolayısıyla, bir veri örneğinin nokta grafiği parabol şeklindeyse, doğrusal regresyon modeli yerine ikinci dereceden regresyon modeli oluşturmak daha iyi olacaktır. Bu şekilde regresyon modeli denklemi veri örneğine daha iyi uyacaktır.

Polinom regresyonun, tıpkı üstel regresyon ve logaritmik regresyon gibi, doğrusal olmayan bir regresyon türü olduğunu unutmayın.

Polinom Regresyon Formülü

Bir polinom regresyon modelinin denklemi şöyledir: y=β ₀ +β ₁ x+β ₂ x ² +β ₃ x ³ …+β _m x ^m +ε.

$y=\beta_0+\beta_1 x+\beta_2 x^2+\beta_3 x^3+\dots+\beta_m x^m+\varepsilon$

Altın:

$y$

bağımlı değişkendir.
$x$

bağımsız değişkendir.
$\beta_0$

polinom regresyon denkleminin sabitidir.
$\beta_i$

değişkenle ilişkili regresyon katsayısıdır

$x^i$

.
$\bm{\varepsilon}$

Bu hata veya artıktır, yani gözlemlenen değer ile model tarafından tahmin edilen değer arasındaki farktır.

Toplamda bir örneğimiz varsa

$n$

gözlemler için polinom regresyon modelini matris biçiminde önerebiliriz:

$\begin{pmatrix}y_1\\y_2\\y_3\\\vdots\\y_n\end{pmatrix}=\begin{pmatrix}1&x_1&x_1^2&\dots&x_1^m\\1&x_2&x_2^2&\dots&x_2^m\\1&x_3&x_3^2&\dots&x_3^m\\ \vdots&\vdots&\ddots&\vdots\\1&x_{n}&x_n^2&\dots&x_n^m\end{pmatrix}\cdot\begin{pmatrix}\beta_0\\\beta_1\\\beta_2\\\vdots\\\beta_m\end{pmatrix}+\begin{pmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\vdots\\\varepsilon_n\end{pmatrix}$

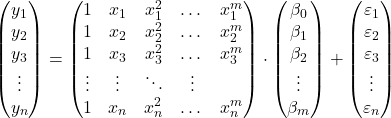
Yukarıdaki matris ifadesi, her matrise bir harf atanarak yeniden yazılabilir:

$Y=X\beta+\varepsilon$

Böylece, en küçük kareler kriterini uygulayarak, bir polinom regresyon modelinin katsayılarını tahmin etmek için kullanılan formüle ulaşabiliriz:

$\widehat{\beta}=\left(X^tX\right)^{-1}X^tY$

Ancak bu hesaplamaları elle yapmak çok zahmetli ve zaman alıcı olduğundan, polinom regresyon modelini çok daha hızlı gerçekleştirmenizi sağlayan bilgisayar yazılımlarını (Minitab veya Excel gibi) kullanmak daha uygundur.

Polinom regresyon modeli örneği

Artık polinom regresyonun tanımını ve nasıl yapıldığını bildiğimize göre, kavramı tam olarak anlamak için gerçek hayattan bir örneğe bakalım.

Öncelikle veri grafiğinin polinom eğrisi şekline sahip olduğu durumlarda polinom regresyon modelinin yapılması gerektiği unutulmamalıdır. Örneğin nokta grafiği kübik eğri şeklindeyse üçüncü dereceden polinom regresyon modeli oluşturmamız gerekir.

Yani aşağıdaki görselde gördüğünüz gibi verilerimizin nokta grafiği ikinci dereceden bir şekle sahip çünkü bağımsız değişkenin değerini artırdıkça bağımlı değişken daha hızlı büyüyor. Bu durumda doğrusal bir regresyon modeli uygulandı ve gördüğünüz gibi noktalara pek iyi uymuyor çünkü çizginin tüm noktaların altında olduğu bölümler ve çizginin bunların üstünde olduğu bölümler var.

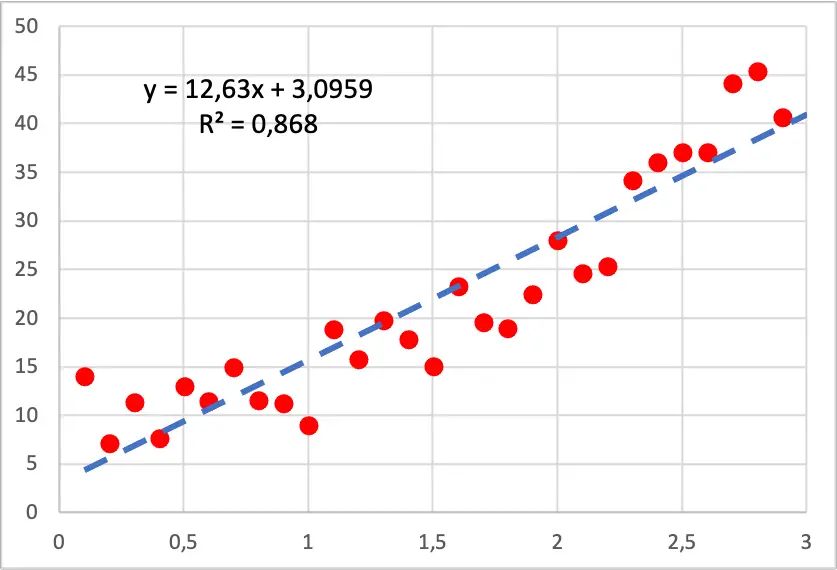
Öte yandan ikinci dereceden polinom regresyon modelini çalıştırırsak aşağıdaki görselde de görebileceğiniz gibi örnek verilere çok daha iyi uyum sağlıyor.

Ayrıca polinom regresyon modeli geliştirilirken belirleme katsayısı %86,80’den %94,05’e çıktığı için oldukça iyileşir. Dolayısıyla yeni regresyon modeli veri setini çok daha iyi açıklamaktadır.

Öte yandan polinom regresyonu yapmamız gerektiğinin bir diğer göstergesi de artıkların grafiğidir. Doğrusal bir regresyonda artıkların grafiği bir parabol veya başka türde bir polinom şeklindeyse, bir polinom regresyon modeli çalışılan verilere kesinlikle daha iyi uyar.

Diğer doğrusal olmayan regresyon türleri

Temel olarak üç tür doğrusal olmayan regresyon vardır:

Polinom Regresyon – Regresyon modeli denklemi bir polinom biçimindedir.
Logaritmik regresyon : Bağımsız değişkenin logaritması alınır.
Üstel Regresyon : Bağımsız değişken denklemin üssünde bulunur.

➤ Bakınız: Logaritmik regresyon
➤ Bakınız: Üstel Regresyon

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil