Python'da eğri uydurma (örneklerle)

Çoğu zaman Python’da bir veri kümesine bir eğri sığdırmak isteyebilirsiniz.

Aşağıdaki adım adım örnek, numpy.polyfit() işlevini kullanarak eğrilerin Python’daki verilere nasıl sığdırılacağını ve verilere en iyi uyan eğrinin nasıl belirleneceğini açıklamaktadır.

1. Adım: Verileri oluşturun ve görselleştirin

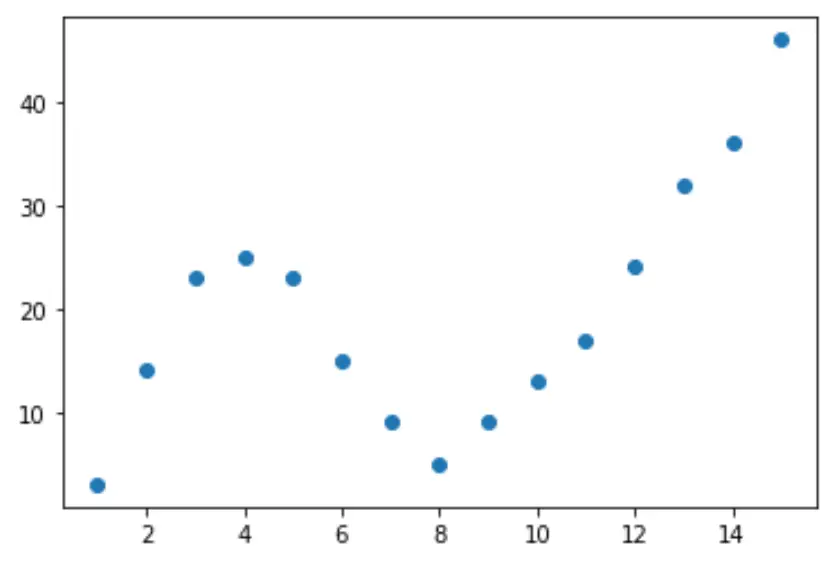
Sahte bir veri kümesi oluşturarak başlayalım, ardından verileri görselleştirmek için bir dağılım grafiği oluşturalım:

 import pandas as pd
import matplotlib. pyplot as plt

#createDataFrame
df = pd. DataFrame ({' x ': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15],
                   ' y ': [3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46]})

#create scatterplot of x vs. y
plt. scatter (df. x , df. y ) 

Adım 2: Birden Fazla Eğriyi Ayarlayın

Daha sonra verilere birkaç polinom regresyon modeli yerleştirelim ve her modelin eğrisini aynı çizimde görselleştirelim:

 import numpy as np

#fit polynomial models up to degree 5
model1 = np. poly1d (np. polyfit (df. x , df. y , 1))
model2 = np. poly1d (np. polyfit (df. x , df. y , 2))
model3 = np. poly1d (np. polyfit (df. x , df. y , 3))
model4 = np. poly1d (np. polyfit (df. x , df. y , 4))
model5 = np. poly1d (np. polyfit (df. x , df. y , 5))

#create scatterplot
polyline = np. linspace (1, 15, 50)
plt. scatter (df. x , df. y )

#add fitted polynomial lines to scatterplot 
plt. plot (polyline, model1(polyline), color=' green ')
plt. plot (polyline, model2(polyline), color=' red ')
plt. plot (polyline, model3(polyline), color=' purple ')
plt. plot (polyline, model4(polyline), color=' blue ')
plt. plot (polyline, model5(polyline), color=' orange ')
plt. show ()

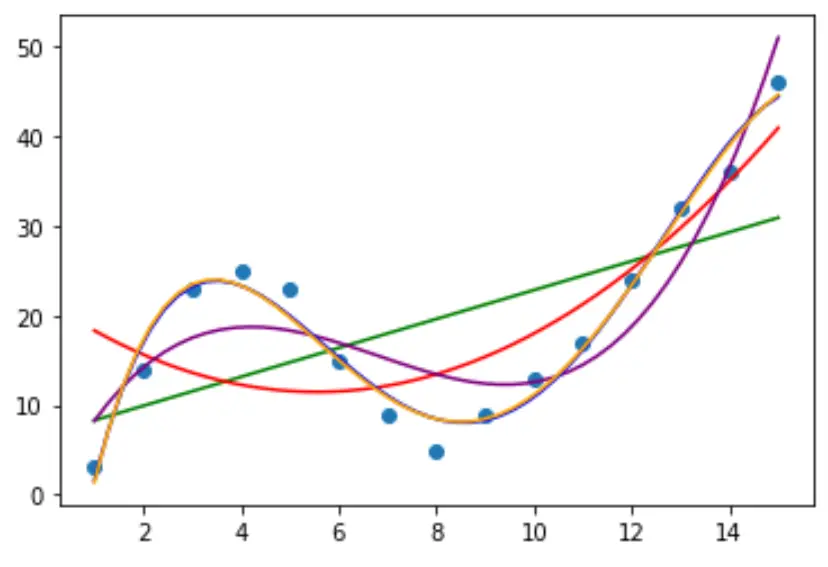
Hangi eğrinin verilere en iyi şekilde uyduğunu belirlemek için her modelin düzeltilmiş R karesine bakabiliriz.

Bu değer bize, yordayıcı değişken sayısına göre ayarlanan, modeldeki yordayıcı değişken(ler) tarafından açıklanabilecek yanıt değişkenindeki varyasyonun yüzdesini belirtir.

 #define function to calculate adjusted r-squared
def adjR(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar)**2)
    sstot = np. sum ((y - ybar)**2)
    results[' r_squared '] = 1- (((1-(ssreg/sstot))*(len(y)-1))/(len(y)-degree-1))

    return results

#calculated adjusted R-squared of each model
adjR(df. x , df. y , 1)
adjR(df. x , df. y , 2)
adjR(df. x , df. y , 3)
adjR(df. x , df. y , 4)
adjR(df. x , df. y , 5)

{'r_squared': 0.3144819}
{'r_squared': 0.5186706}
{'r_squared': 0.7842864}
{'r_squared': 0.9590276}
{'r_squared': 0.9549709}

Sonuçtan, en yüksek düzeltilmiş R-kare değerine sahip modelin, düzeltilmiş R-kare değeri 0,959 olan dördüncü derece polinom olduğunu görebiliriz.

3. Adım: Son eğriyi görselleştirin

Son olarak dördüncü derece polinom modelinin eğrisiyle bir dağılım grafiği oluşturabiliriz:

 #fit fourth-degree polynomial
model4 = np. poly1d (np. polyfit (df. x , df. y , 4))

#define scatterplot
polyline = np. linspace (1, 15, 50)
plt. scatter (df. x , df. y )

#add fitted polynomial curve to scatterplot
plt. plot (polyline, model4(polyline), ' -- ', color=' red ')
plt. show ()

Bu satırın denklemini print() fonksiyonunu kullanarak da elde edebiliriz:

 print (model4)

          4 3 2
-0.01924x + 0.7081x - 8.365x + 35.82x - 26.52

Eğrinin denklemi aşağıdaki gibidir:

y = -0,01924x ⁴ + 0,7081x ³ – 8,365x ² + 35,82x – 26,52

Bu denklemi, modeldeki yordayıcı değişkenlere dayalı olarak yanıt değişkeninin değerini tahmin etmek için kullanabiliriz. Örneğin, eğer x = 4 ise y = 23,32 olacağını tahmin ederiz:

y = -0,0192(4) ⁴ + 0,7081(4) ³ – 8,365(4) ² + 35,82(4) – 26,52 = 23,32

Ek kaynaklar

Polinom Regresyona Giriş
Python’da polinom regresyonu nasıl gerçekleştirilir