Python'da normallik nasıl test edilir (4 yöntem)

Birçok istatistiksel test, veri setlerinin normal şekilde dağıldığını varsayar .

Python’da bu hipotezi kontrol etmenin dört yaygın yolu vardır:

1. (Görsel yöntem) Bir histogram oluşturun.

• Histogram yaklaşık olarak “çan” şeklindeyse verilerin normal dağıldığı varsayılır.

2. (Görsel yöntem) Bir QQ grafiği oluşturun.

• Grafikteki noktalar kabaca düz bir çapraz çizgi boyunca uzanıyorsa, verilerin normal dağıldığı varsayılır.

3. (Resmi istatistiksel test) Shapiro-Wilk testi yapın.

• Testin p değeri α = 0,05’ten büyükse verilerin normal dağıldığı varsayılır.

4. (Resmi istatistiksel test) Kolmogorov-Smirnov testini yapın.

• Testin p değeri α = 0,05’ten büyükse verilerin normal dağıldığı varsayılır.

Aşağıdaki örnekler bu yöntemlerin her birinin pratikte nasıl kullanılacağını göstermektedir.

Yöntem 1: Histogram Oluşturma

Aşağıdaki kod, log-normal dağılımı izleyen bir veri kümesi için histogramın nasıl oluşturulacağını gösterir:

 import math
import numpy as np
from scipy. stats import lognorm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create histogram to visualize values in dataset
plt. hist (lognorm_dataset, edgecolor=' black ', bins=20) 

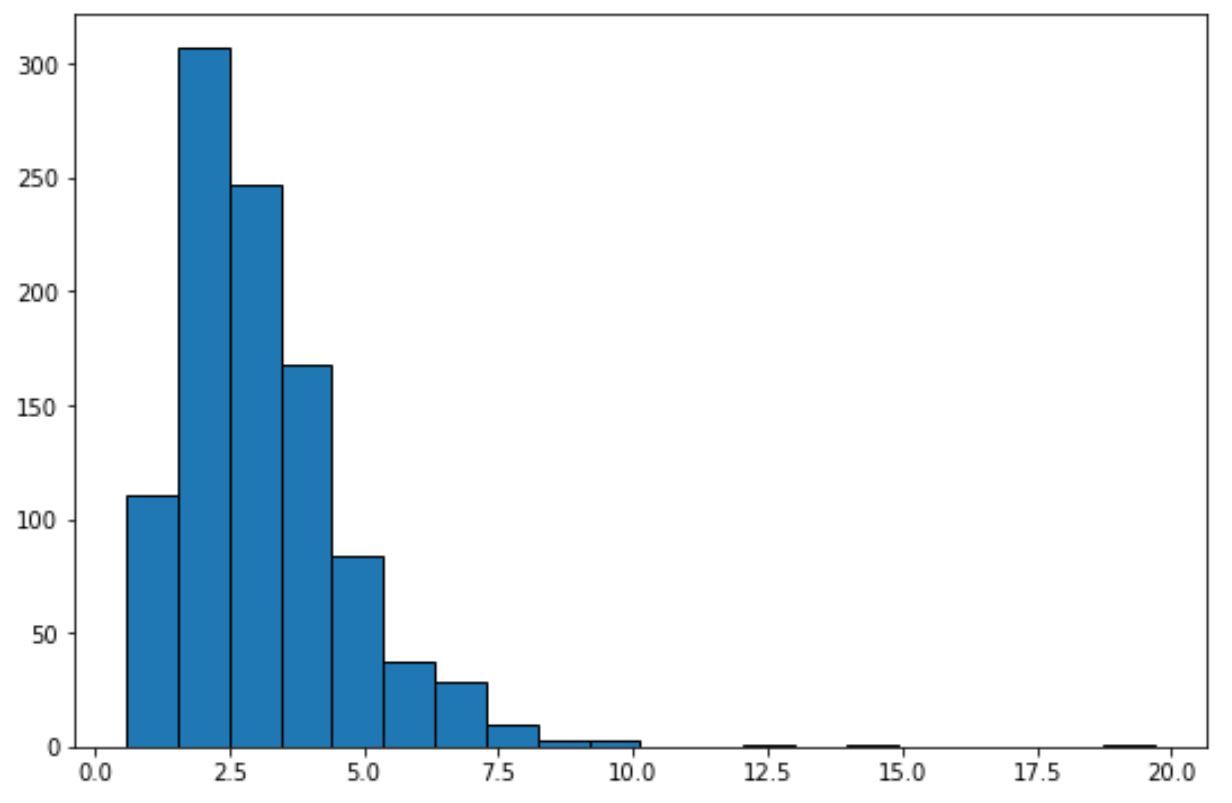
Sadece bu histograma bakarak veri setinin “çan şekli” sergilemediğini ve normal dağılmadığını söyleyebiliriz.

Yöntem 2: QQ Grafiği Oluşturma

Aşağıdaki kod, log-normal dağılımı izleyen bir veri kümesi için QQ grafiğinin nasıl oluşturulacağını gösterir:

 import math
import numpy as np
from scipy. stats import lognorm
import statsmodels. api as sm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create QQ plot with 45-degree line added to plot
fig = sm. qqplot (lognorm_dataset, line=' 45 ')

plt. show ()

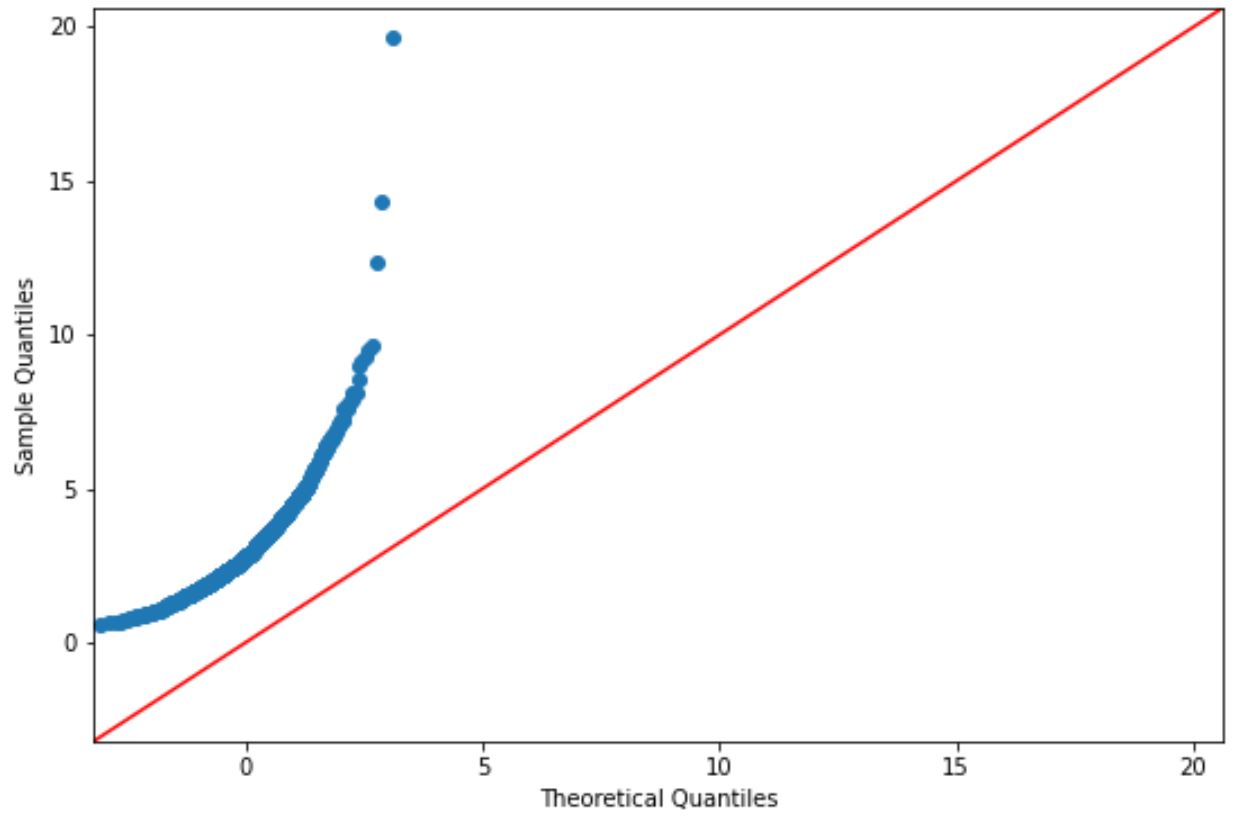
Çizim noktaları yaklaşık olarak düz bir çapraz çizgi boyunca uzanıyorsa, genellikle bir veri kümesinin normal şekilde dağıldığını varsayarız.

Ancak bu grafikteki noktalar açıkça kırmızı çizgiye karşılık gelmiyor, dolayısıyla bu veri setinin normal dağıldığını varsayamayız.

Verileri log-normal dağılım fonksiyonunu kullanarak oluşturduğumuz göz önüne alındığında, bu mantıklı olmalıdır.

Yöntem 3: Shapiro-Wilk testi gerçekleştirin

Aşağıdaki kod, log-normal dağılımı izleyen bir veri kümesi için Shapiro-Wilk’in nasıl gerçekleştirileceğini gösterir:

 import math
import numpy as np
from scipy.stats import shapiro 
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Shapiro-Wilk test for normality
shapiro(lognorm_dataset)

ShapiroResult(statistic=0.8573324680328369, pvalue=3.880663073872444e-29)

Sonuçtan test istatistiğinin 0,857 olduğunu ve buna karşılık gelen p değerinin 3,88e-29 (sıfıra son derece yakın) olduğunu görebiliriz.

P değeri 0,05’ten küçük olduğundan Shapiro-Wilk testinin sıfır hipotezini reddediyoruz.

Bu, örnek verilerin normal dağılımdan gelmediğini söyleyecek yeterli kanıtımız olduğu anlamına gelir.

Yöntem 4: Kolmogorov-Smirnov testi yapın

Aşağıdaki kod, log-normal dağılımı izleyen bir veri kümesi için Kolmogorov-Smirnov testinin nasıl gerçekleştirileceğini gösterir:

 import math
import numpy as np
from scipy.stats import kstest
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Kolmogorov-Smirnov test for normality
kstest(lognorm_dataset, ' norm ')

KstestResult(statistic=0.84125708308077, pvalue=0.0)

Sonuçtan test istatistiğinin 0,841 ve buna karşılık gelen p değerinin 0,0 olduğunu görebiliriz.

P değeri 0,05’ten küçük olduğundan Kolmogorov-Smirnov testinin sıfır hipotezini reddediyoruz.

Bu, örnek verilerin normal dağılımdan gelmediğini söyleyecek yeterli kanıtımız olduğu anlamına gelir.

Normal olmayan veriler nasıl işlenir?

Belirli bir veri kümesi normal şekilde dağılmıyorsa , onu daha normal bir şekilde dağıtmak için genellikle aşağıdaki dönüşümlerden birini gerçekleştirebiliriz:

1. Log dönüşümü: x değerlerini log(x)’ e dönüştürün.

2. Karekök dönüşümü: x’in değerlerini √x’e dönüştürün.

3. Küp kök dönüşümü: x’in değerlerini x ^1/3’e dönüştürün.

Bu dönüşümlerin gerçekleştirilmesiyle veri kümesi genel olarak daha normal dağılmış hale gelir.

Bu dönüşümlerin Python’da nasıl gerçekleştirileceğini görmek için bu öğreticiyi okuyun.