Python'da kısmi en küçük kareler (adım adım)

Makine öğreniminde karşılaşacağınız en yaygın sorunlardan biri çoklu bağlantıdır . Bu, bir veri setindeki iki veya daha fazla öngörücü değişkenin yüksek düzeyde korelasyona sahip olması durumunda ortaya çıkar.

Bu gerçekleştiğinde, bir model bir eğitim veri setine iyi uyum sağlayabilir ancak eğitim veri setine fazla uyum sağladığı için daha önce görmediği yeni bir veri setinde düşük performans gösterebilir. Eğitim Seti.

Bu sorunu aşmanın bir yolu , kısmi en küçük kareler adı verilen ve şu şekilde çalışan bir yöntem kullanmaktır:

• Tahmin edici ve yanıt değişkenlerini standartlaştırın.
• Hem yanıt değişkenindeki hem de yordayıcı değişkenlerdeki önemli miktarda varyasyonu açıklayan p orijinal yordayıcı değişkenin M doğrusal kombinasyonunu (“PLS bileşenleri” olarak adlandırılır) hesaplayın .
• Tahmin edici olarak PLS bileşenlerini kullanarak doğrusal bir regresyon modeline uymak için en küçük kareler yöntemini kullanın.
• Modelde tutulacak en uygun PLS bileşeni sayısını bulmak için k-katlı çapraz doğrulamayı kullanın.

Bu eğitimde Python’da kısmi en küçük karelerin nasıl gerçekleştirileceğine ilişkin adım adım bir örnek sunulmaktadır.

Adım 1: Gerekli paketleri içe aktarın

İlk olarak Python’da kısmi en küçük kareler gerçekleştirmek için gereken paketleri içe aktaracağız:

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn. model_selection import train_test_split
from sklearn. cross_decomposition import PLSRegression
from sklearn . metrics import mean_squared_error

2. Adım: Verileri yükleyin

Bu örnek için mtcars adı verilen ve 33 farklı araba hakkında bilgi içeren bir veri kümesi kullanacağız. Yanıt değişkeni olarak hp’yi ve yordayıcılar olarak aşağıdaki değişkenleri kullanacağız:

• mpg
• görüntülemek
• bok
• ağırlık
• qsec

Aşağıdaki kod bu veri kümesinin nasıl yüklenip görüntüleneceğini gösterir:

 #define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

Adım 3: Kısmi en küçük kareler modelini yerleştirin

Aşağıdaki kod, PLS modelinin bu verilere nasıl sığdırılacağını gösterir.

cv = RepeatedKFold() fonksiyonunun Python’a model performansını değerlendirmek için k-katlı çapraz doğrulama kullanmasını söylediğini unutmayın . Bu örnek için k = 10 kat seçiyoruz, bu 3 kez tekrarlanıyor.

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#define cross-validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

mse = []
n = len (X)

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (PLSRegression(n_components=1),
n.p. ones ((n,1)), y, cv=cv, scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    pls = PLSRegression(n_components=i)
    score = -1*model_selection. cross_val_score (pls, scale(X), y, cv=cv,
               scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)

#plot test MSE vs. number of components
plt. plot (mse)
plt. xlabel (' Number of PLS Components ')
plt. ylabel (' MSE ')
plt. title (' hp ')

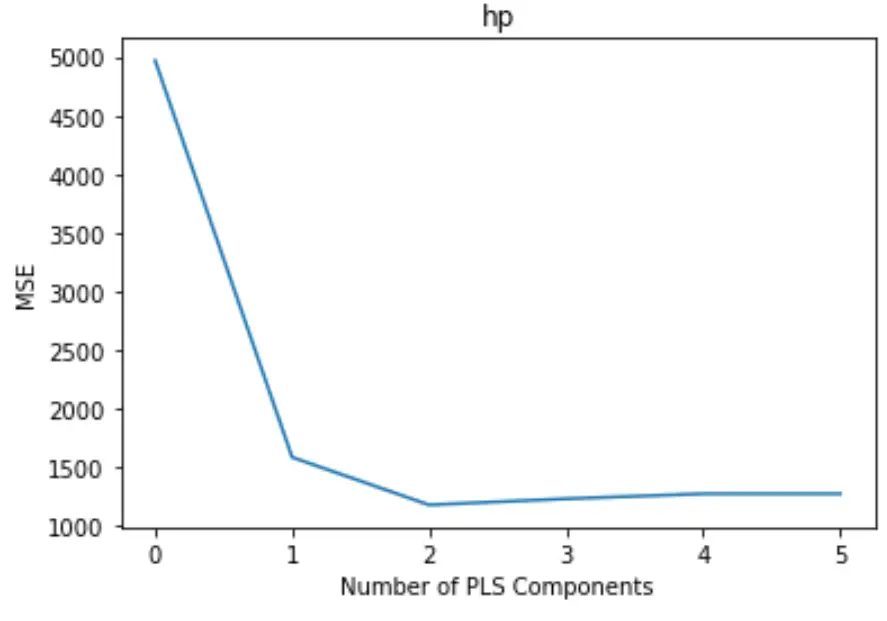
Grafik, x ekseni boyunca PLS bileşenlerinin sayısını ve y ekseni boyunca MSE (ortalama kare hatası) testini gösterir.

Grafikten, testin MSE’sinin iki PLS bileşeni eklediğimizde azaldığını, ancak ikiden fazla PLS bileşeni ekledikçe artmaya başladığını görebiliyoruz.

Bu nedenle optimal model yalnızca ilk iki PLS bileşenini içerir.

Adım 4: Tahminlerde bulunmak için son modeli kullanın

Yeni gözlemler hakkında tahminlerde bulunmak için son PLS modelini iki PLS bileşeniyle kullanabiliriz.

Aşağıdaki kod, orijinal veri setinin bir eğitim ve test setine nasıl bölüneceğini ve test seti üzerinde tahminler yapmak için PLS modelinin iki PLS bileşeniyle nasıl kullanılacağını gösterir.

 #split the dataset into training (70%) and testing (30%) sets
X_train , _

#calculate RMSE
pls = PLSRegression(n_components=2)
pls. fit (scale(X_train), y_train)

n.p. sqrt (mean_squared_error(y_test, pls. predict (scale(X_test))))

29.9094

Testin RMSE’sinin 29,9094 olduğunu görüyoruz. Bu, test seti gözlemleri için tahmin edilen hp değeri ile gözlenen hp değeri arasındaki ortalama sapmadır.

Bu örnekte kullanılan Python kodunun tamamını burada bulabilirsiniz.