Python'da i̇ki değişkenli analiz nasıl gerçekleştirilir: örneklerle

İki değişkenli analiz terimi, iki değişkenin analizini ifade eder. Bunu “bi” ön ekinin “iki” anlamına gelmesinden dolayı hatırlayabilirsiniz.

İki değişkenli analizin amacı iki değişken arasındaki ilişkiyi anlamaktır.

İki değişkenli analiz gerçekleştirmenin üç yaygın yolu vardır:

1. Nokta bulutları

2. Korelasyon katsayıları

3. Basit doğrusal regresyon

Aşağıdaki örnek, iki değişken hakkında bilgi içeren aşağıdaki pandalar DataFrame’i kullanarak Python’da bu iki değişkenli analiz türlerinin her birinin nasıl gerçekleştirileceğini gösterir: (1) Çalışmak için harcanan saatler ve (2) 20 farklı öğrenci tarafından alınan sınav puanı:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                             3, 4, 4, 5, 5, 6, 6, 6, 7, 8],
                   ' score ': [75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                             80, 88, 85, 90, 92, 94, 94, 88, 91, 96]})

#view first five rows of DataFrame
df. head ()

	hours score
0 1 75
1 1 66
2 1 68
3 2 74
4 2 78

1. Nokta bulutları

Sınav sonuçlarına karşı çalışılan saatlerin dağılım grafiğini oluşturmak için aşağıdaki sözdizimini kullanabiliriz:

 import matplotlib. pyplot as plt

#create scatterplot of hours vs. score
plt. scatter (df. hours , df. score )
plt. title (' Hours Studied vs. Exam Score ')
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

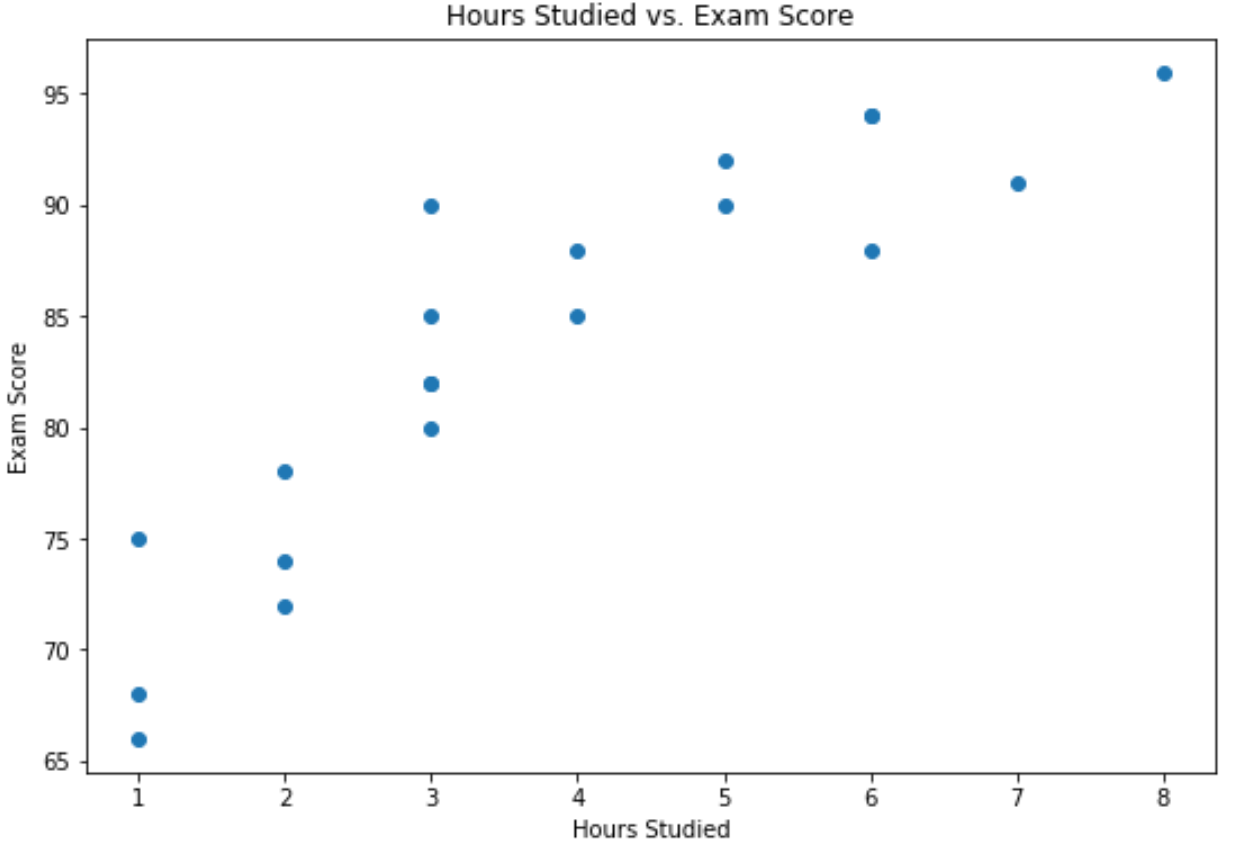
X ekseni çalışılan saatleri, y ekseni ise sınavda alınan notu gösterir.

Grafik, iki değişken arasında pozitif bir ilişki olduğunu göstermektedir: Çalışma saati arttıkça sınav puanları da artma eğilimindedir.

2. Korelasyon katsayıları

Pearson korelasyon katsayısı, iki değişken arasındaki doğrusal ilişkiyi ölçmenin bir yoludur.

Korelasyon matrisi oluşturmak için pandalarda corr() fonksiyonunu kullanabiliriz:

 #create correlation matrix
df. corr ()

	hours score
hours 1.000000 0.891306
score 0.891306 1.000000

Korelasyon katsayısı 0,891 olarak çıkıyor. Bu, çalışılan saat ile sınav notu arasında güçlü bir pozitif korelasyon olduğunu gösterir.

3. Basit doğrusal regresyon

Basit doğrusal regresyon, iki değişken arasındaki ilişkiyi ölçmek için kullanabileceğimiz istatistiksel bir yöntemdir.

Çalışılan saatler ve alınan sınav sonuçları için basit bir doğrusal regresyon modelini hızlı bir şekilde uyarlamak amacıyla statsmodels paketindeki OLS() işlevini kullanabiliriz:

 import statsmodels. api as sm

#define response variable
y = df[' score ']

#define explanatory variable
x = df[[' hours ']]

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.794
Model: OLS Adj. R-squared: 0.783
Method: Least Squares F-statistic: 69.56
Date: Mon, 22 Nov 2021 Prob (F-statistic): 1.35e-07
Time: 16:15:52 Log-Likelihood: -55,886
No. Observations: 20 AIC: 115.8
Df Residuals: 18 BIC: 117.8
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 69.0734 1.965 35.149 0.000 64.945 73.202
hours 3.8471 0.461 8.340 0.000 2.878 4.816
==================================================== ============================
Omnibus: 0.171 Durbin-Watson: 1.404
Prob(Omnibus): 0.918 Jarque-Bera (JB): 0.177
Skew: 0.165 Prob(JB): 0.915
Kurtosis: 2.679 Cond. No. 9.37
==================================================== ============================

Uygun regresyon denklemi şu şekilde ortaya çıkıyor:

Sınav puanı = 69,0734 + 3,8471*(çalışma saati)

Bu bize, çalışılan her ek saatin sınav puanında ortalama 3,8471 artışla ilişkili olduğunu söylüyor.

Bir öğrencinin toplam ders saatine göre alacağı puanı tahmin etmek için uygun regresyon denklemini de kullanabiliriz.

Örneğin 3 saat ders çalışan bir öğrencinin 81.6147 puan alması gerekir:

• Sınav puanı = 69,0734 + 3,8471*(çalışma saati)
• Sınav puanı = 69,0734 + 3,8471*(3)
• Sınav sonucu = 81.6147

Ek kaynaklar

Aşağıdaki eğitimler iki değişkenli analiz hakkında ek bilgi sağlar:

İki Değişkenli Analize Giriş
Gerçek hayatta iki değişkenli verilere 5 örnek
Basit Doğrusal Regresyona Giriş
Pearson Korelasyon Katsayısına Giriş