Python'da niceliksel regresyon nasıl gerçekleştirilir

Doğrusal regresyon, bir veya daha fazla yordayıcı değişken ile bir yanıt değişkeni arasındaki ilişkiyi anlamak için kullanabileceğimiz bir yöntemdir.

Tipik olarak doğrusal regresyon uyguladığımızda yanıt değişkeninin ortalama değerini tahmin etmek isteriz.

Bununla birlikte, yanıt değerinin herhangi bir nicelik veya yüzdelik değerini (70. yüzdelik dilim, 90. yüzdelik dilim, 98. yüzdelik dilim vb.) tahmin etmek için bunun yerine nicelik regresyonu olarak bilinen bir yöntemi kullanabiliriz.

Bu eğitimde, Python’da niceliksel regresyon gerçekleştirmek için bu işlevin nasıl kullanılacağına ilişkin adım adım bir örnek sunulmaktadır.

Adım 1: Gerekli paketleri yükleyin

Öncelikle gerekli paketleri ve fonksiyonları yükleyeceğiz:

 import numpy as np
import pandas as pd
import statsmodels. api as sm
import statsmodels. formula . api as smf
import matplotlib. pyplot as plt

2. Adım: Verileri oluşturun

Bu örnek için bir üniversitede 100 öğrencinin ders çalışma saatlerini ve aldıkları sınav sonuçlarını içeren bir veri seti oluşturacağız:

 #make this example reproducible
n.p. random . seeds (0)

#create dataset
obs = 100

hours = np. random . uniform (1, 10, obs)
score = 60 + 2*hours + np. random . normal (loc=0, scale=.45*hours, size=100)

df = pd. DataFrame ({' hours ':hours, ' score ':score})

#view first five rows
df. head ()

hours score
0 5.939322 68.764553
1 7.436704 77.888040
2 6.424870 74.196060
3 5.903949 67.726441
4 4.812893 72.849046

Adım 3: Kantil Regresyon Gerçekleştirin

Daha sonra, yordayıcı değişken olarak çalışılan saatleri ve yanıt değişkeni olarak sınav puanlarını kullanarak niceliksel bir regresyon modeli uygulayacağız.

Bu modeli, çalışılan saat sayısına bağlı olarak sınav puanlarının beklenen yüzde 90’lık dilimini tahmin etmek için kullanacağız:

 #fit the model
model = smf. quantreg ('score~hours', df). fit (q= 0.9 )

#view model summary
print ( model.summary ())

                         QuantReg Regression Results                          
==================================================== ============================
Dept. Variable: Pseudo R-squared score: 0.6057
Model: QuantReg Bandwidth: 3.822
Method: Least Squares Sparsity: 10.85
Date: Tue, 29 Dec 2020 No. Observations: 100
Time: 15:41:44 Df Residuals: 98
                                        Model: 1
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
Intercept 59.6104 0.748 79.702 0.000 58.126 61.095
hours 2.8495 0.128 22.303 0.000 2.596 3.103
==================================================== ============================

Sonuçtan tahmini regresyon denklemini görebiliriz:

Sınav puanının 90. yüzdelik dilimi = 59,6104 + 2,8495*(saat)

Örneğin 8 saat ders çalışan tüm öğrencilerin 90. yüzdelik puanı 82,4 olmalıdır:

Sınav puanının 90. yüzdelik dilimi = 59,6104 + 2,8495*(8) = 82,4 .

Çıktı ayrıca tahmin değişkeninin kesişme noktası ve süreleri için üst ve alt güven sınırlarını da görüntüler.

4. Adım: Sonuçları görselleştirin

Grafiğe yerleştirilmiş niceliksel regresyon denklemi ile bir dağılım grafiği oluşturarak regresyon sonuçlarını da görselleştirebiliriz:

 #define figure and axis
fig, ax = plt.subplots(figsize=(8, 6))

#get y values
get_y = lambda a, b: a + b * hours
y = get_y( model.params [' Intercept '], model.params [' hours '])

#plot data points with quantile regression equation overlaid
ax. plot (hours, y, color=' black ')
ax. scatter (hours, score, alpha=.3)
ax. set_xlabel (' Hours Studied ', fontsize=14)
ax. set_ylabel (' Exam Score ', fontsize=14)

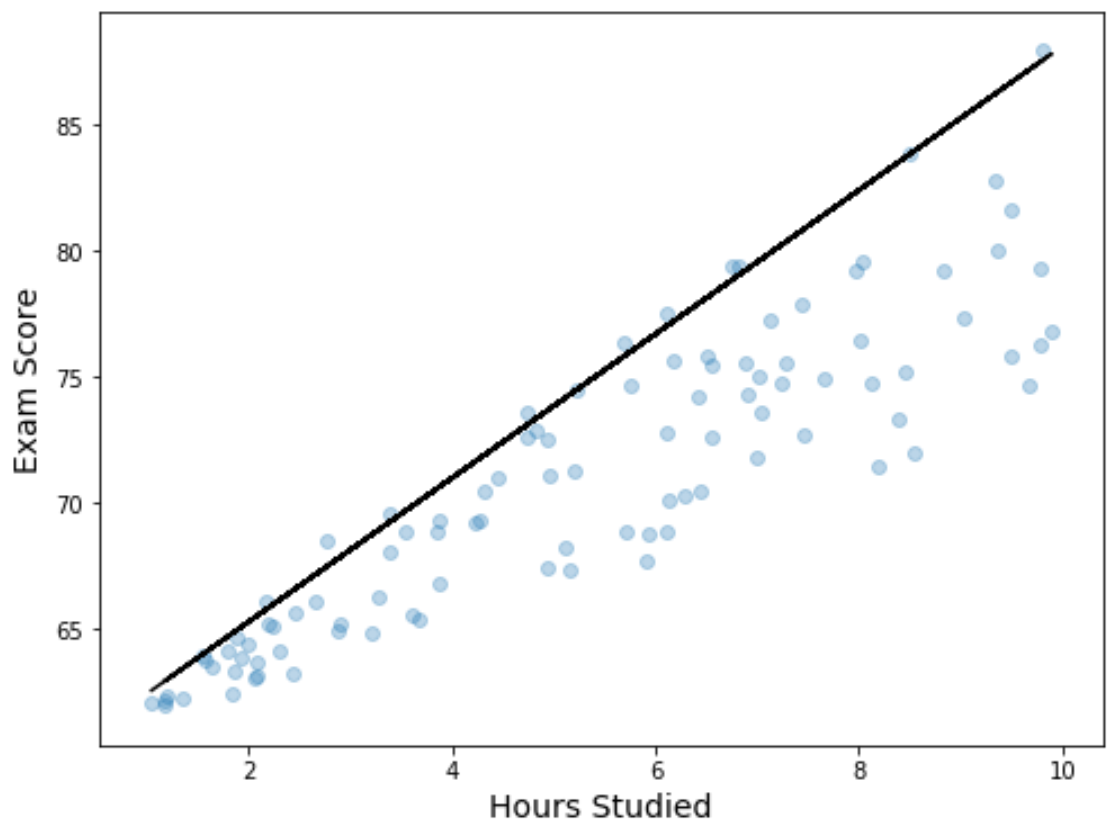
Basit bir doğrusal regresyon çizgisinin aksine, bu uydurulmuş çizginin veriler için “en iyi uyum çizgisini” temsil etmediğine dikkat edin. Bunun yerine, yordayıcı değişkenin her düzeyinde tahmini 90. yüzdelik dilimden geçer.

Ek kaynaklar

Python’da basit doğrusal regresyon nasıl gerçekleştirilir
Python’da ikinci dereceden regresyon nasıl gerçekleştirilir?