R'de ağırlıklı en küçük kareler regresyonu nasıl gerçekleştirilir

Doğrusal regresyonun temel varsayımlarından biri, artıkların , yordayıcı değişkenin her düzeyinde eşit varyansla dağıldığıdır. Bu varsayıma eş varyanslılık denir.

Bu varsayıma uyulmadığı takdirde artıklarda değişen varyansın mevcut olduğu söylenir. Bu durumda regresyon sonuçları güvenilmez hale gelir.

Bu sorunu çözmenin bir yolu, ağırlıklı en küçük kareler regresyonunu kullanmaktır; bu regresyon, gözlemlere ağırlıklar atayarak, düşük hata varyansına sahip olanların, daha büyük hata varyansına sahip gözlemlere kıyasla daha fazla bilgi içerdiklerinden daha fazla ağırlık almasını sağlar.

Bu eğitimde, R’de ağırlıklı en küçük kareler regresyonunun nasıl gerçekleştirileceğine ilişkin adım adım bir örnek sağlanmaktadır.

1. Adım: Verileri oluşturun

Aşağıdaki kod, 16 öğrenci için çalışılan saat sayısını ve ilgili sınav puanını içeren bir veri çerçevesi oluşturur:

 df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
                 score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))

Adım 2: Doğrusal Regresyon Gerçekleştirin

Daha sonra, tahmin değişkeni olarak saatleri ve yanıt değişkeni olarak puanı kullanan basit bir doğrusal regresyon modeline uyum sağlamak için lm() işlevini kullanacağız:

 #fit simple linear regression model
model <- lm(score ~ hours, data = df)

#view summary of model
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-17,967 -5,970 -0.719 7,531 15,032 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 60,467 5,128 11,791 1.17e-08 ***
hours 5,500 1,127 4,879 0.000244 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 9.224 on 14 degrees of freedom
Multiple R-squared: 0.6296, Adjusted R-squared: 0.6032 
F-statistic: 23.8 on 1 and 14 DF, p-value: 0.0002438

Adım 3: Heteroskedasticliği test edin

Daha sonra, heteroskedastisiteyi görsel olarak kontrol etmek için artıkların ve uydurulmuş değerlerin bir grafiğini oluşturacağız:

 #create residual vs. fitted plot
plot( fitted (model), resid (model), xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

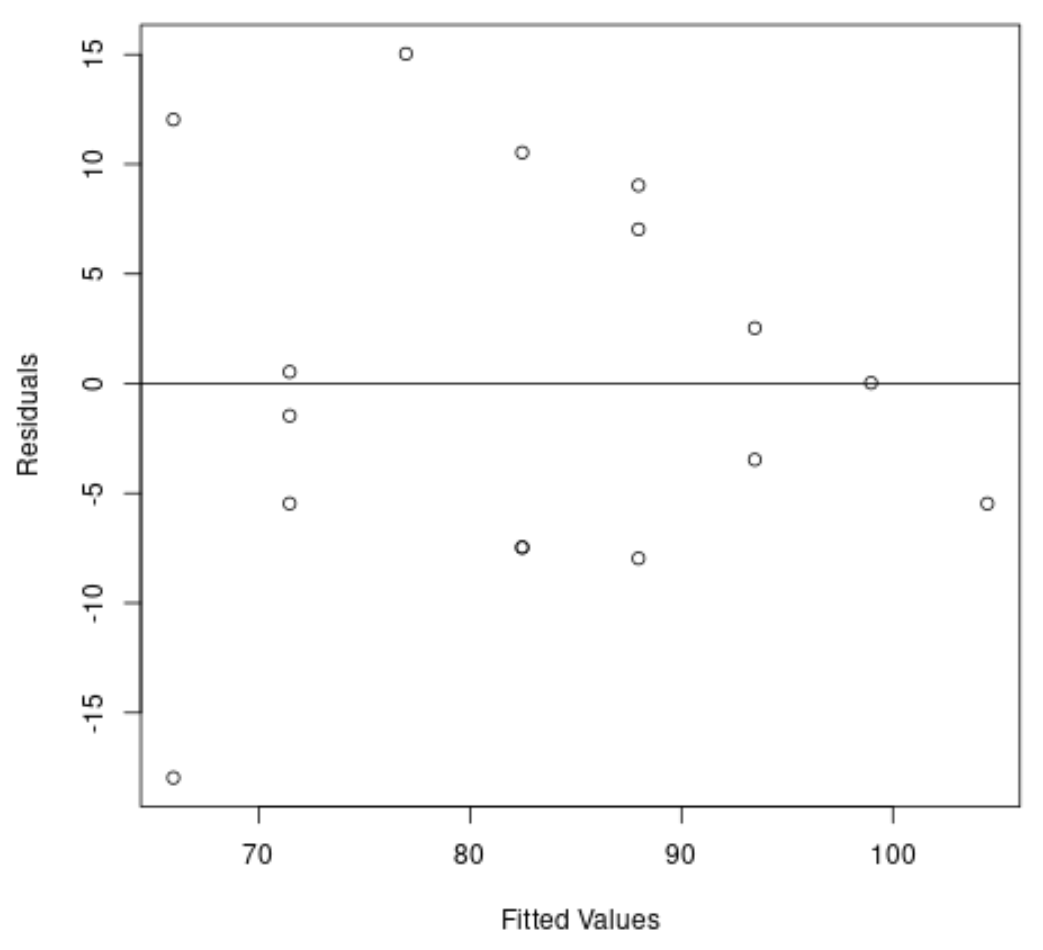
Artıkların “koni” şekline sahip olduğunu grafikten görebiliriz: grafik boyunca eşit varyansla dağılmazlar.

Değişen varyanslılığı resmi olarak test etmek için Breusch-Pagan testi yapabiliriz:

 #load lmtest package
library (lmtest)

#perform Breusch-Pagan test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 3.9597, df = 1, p-value = 0.0466

Breusch-Pagan testi aşağıdaki boş ve alternatif hipotezleri kullanır:

• Boş hipotez (H ₀ ): Eş varyans mevcut (artıklar eşit varyansla dağıtılıyor)
• Alternatif hipotez ( _HA ): değişen varyans mevcut (artıklar eşit varyansla dağılmıyor)

Testin p değeri 0,0466 olduğundan sıfır hipotezini reddedeceğiz ve değişen varyansın bu modelde bir sorun olduğu sonucuna varacağız.

Adım 4: Ağırlıklı en küçük kareler regresyonunu gerçekleştirin

Değişen varyans mevcut olduğundan, ağırlıkları daha düşük varyansa sahip gözlemlerin daha fazla ağırlık alacağı şekilde ayarlayarak ağırlıklı en küçük kareler uygulayacağız:

 #define weights to use
wt <- 1 / lm( abs (model$residuals) ~ model$fitted. values )$fitted. values ^2

#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)

#view summary of model
summary(wls_model)

Call:
lm(formula = score ~ hours, data = df, weights = wt)

Weighted Residuals:
    Min 1Q Median 3Q Max 
-2.0167 -0.9263 -0.2589 0.9873 1.6977 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.9689 5.1587 12.400 6.13e-09 ***
hours 4.7091 0.8709 5.407 9.24e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared: 0.6762, Adjusted R-squared: 0.6531 
F-statistic: 29.24 on 1 and 14 DF, p-value: 9.236e-05

Sonuçlardan, saat yordayıcısı değişkenine ilişkin katsayı tahmininin biraz değiştiğini ve genel model uyumunun iyileştiğini görebiliriz.

Ağırlıklandırılmış en küçük kareler modeli, orijinal basit doğrusal regresyon modelindeki 9,224’e kıyasla 1,199’luk bir artık standart hataya sahiptir.

Bu, ağırlıklı en küçük kareler modelinin ürettiği tahmin edilen değerlerin, basit doğrusal regresyon modelinin ürettiği tahmin edilen değerlerle karşılaştırıldığında gerçek gözlemlere çok daha yakın olduğunu gösterir.

Ağırlıklandırılmış en küçük kareler modeli aynı zamanda orijinal basit doğrusal regresyon modelindeki 0,6296’ya kıyasla 0,6762’lik bir R-kare değerine sahiptir.

Bu, ağırlıklı en küçük kareler modelinin, basit doğrusal regresyon modeline göre sınav puanlarındaki varyansı daha fazla açıklayabildiğini gösterir.

Bu ölçümler, ağırlıklı en küçük kareler modelinin, basit doğrusal regresyon modeline kıyasla verilere daha iyi uyum sağladığını göstermektedir.

Ek kaynaklar

R’de basit doğrusal regresyon nasıl gerçekleştirilir
R’de çoklu doğrusal regresyon nasıl gerçekleştirilir
R’de niceliksel regresyon nasıl gerçekleştirilir