R'de eğri uydurma (örneklerle)

Çoğunlukla R eğrisine en iyi uyan denklemi bulmak isteyebilirsiniz.

Aşağıdaki adım adım örnek, poly() işlevini kullanarak eğrilerin R’deki verilere nasıl sığdırılacağını ve verilere en iyi uyan eğrinin nasıl belirleneceğini açıklamaktadır.

1. Adım: Verileri oluşturun ve görselleştirin

Sahte bir veri kümesi oluşturarak başlayalım, ardından verileri görselleştirmek için bir dağılım grafiği oluşturalım:

 #create data frame
df <- data. frame (x=1:15,
                 y=c(3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46))

#create a scatterplot of x vs. y
plot(df$x, df$y, pch= 19 , xlab=' x ', ylab=' y ') 

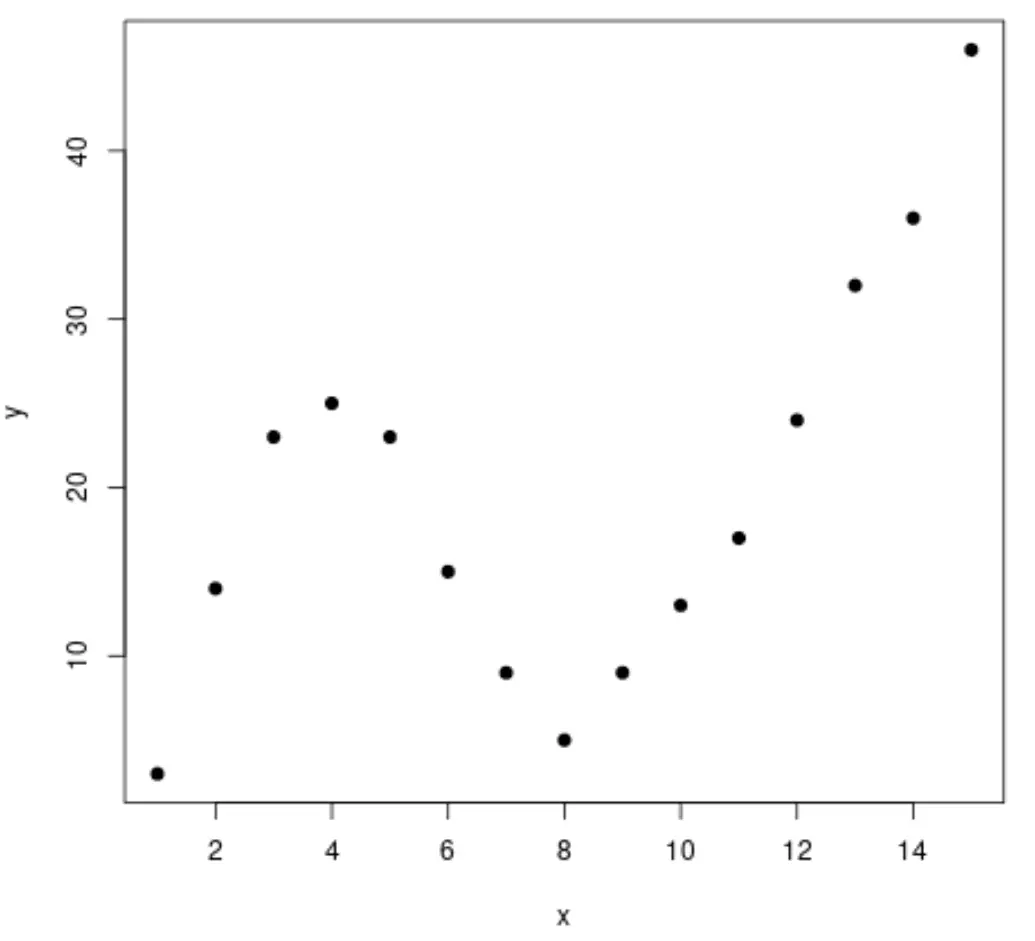
Adım 2: Birden Fazla Eğriyi Ayarlayın

Daha sonra verilere birkaç polinom regresyon modeli yerleştirelim ve her modelin eğrisini aynı çizimde görselleştirelim:

 #fit polynomial regression models up to degree 5
fit1 <- lm(y~x, data=df)
fit2 <- lm(y~poly(x,2,raw= TRUE ), data=df)
fit3 <- lm(y~poly(x,3,raw= TRUE ), data=df)
fit4 <- lm(y~poly(x,4,raw= TRUE ), data=df)
fit5 <- lm(y~poly(x,5,raw= TRUE ), data=df)

#create a scatterplot of x vs. y
plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ')

#define x-axis values
x_axis <- seq(1, 15, length= 15 )

#add curve of each model to plot
lines(x_axis, predict(fit1, data. frame (x=x_axis)), col=' green ')
lines(x_axis, predict(fit2, data. frame (x=x_axis)), col=' red ')
lines(x_axis, predict(fit3, data. frame (x=x_axis)), col=' purple ')
lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ')
lines(x_axis, predict(fit5, data. frame (x=x_axis)), col=' orange ')

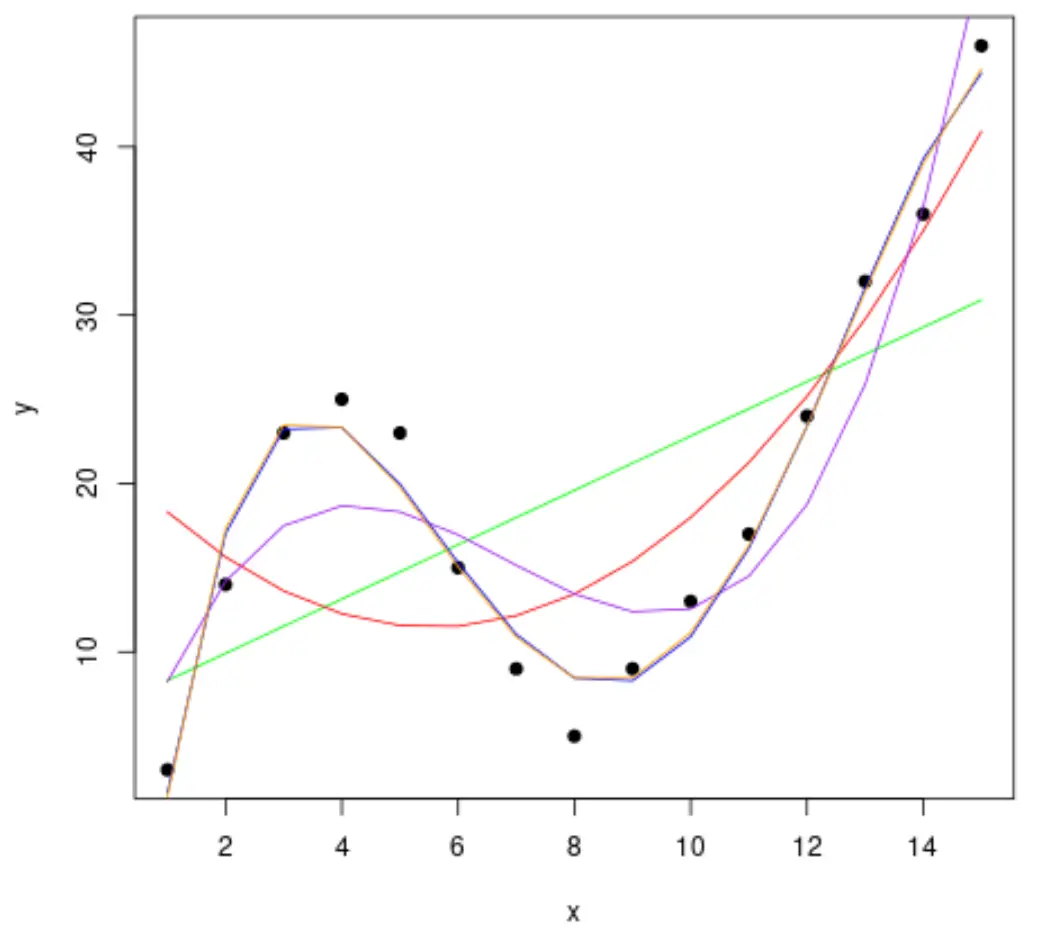
Hangi eğrinin verilere en iyi şekilde uyduğunu belirlemek için her modelin düzeltilmiş R karesine bakabiliriz.

Bu değer bize, yordayıcı değişken sayısına göre ayarlanan, modeldeki yordayıcı değişken(ler) tarafından açıklanabilecek yanıt değişkenindeki varyasyonun yüzdesini belirtir.

 #calculated adjusted R-squared of each model
summary(fit1)$adj. r . squared
summary(fit2)$adj. r . squared
summary(fit3)$adj. r . squared
summary(fit4)$adj. r . squared
summary(fit5)$adj. r . squared

[1] 0.3144819
[1] 0.5186706
[1] 0.7842864
[1] 0.9590276
[1] 0.9549709

Sonuçtan, en yüksek düzeltilmiş R-kare değerine sahip modelin, düzeltilmiş R-kare değeri 0,959 olan dördüncü derece polinom olduğunu görebiliriz.

3. Adım: Son eğriyi görselleştirin

Son olarak dördüncü derece polinom modelinin eğrisiyle bir dağılım grafiği oluşturabiliriz:

 #create a scatterplot of x vs. y
plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ')

#define x-axis values
x_axis <- seq(1, 15, length= 15 )

#add curve of fourth-degree polynomial model
lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ')

Bu satırın denklemini aynı zamanda Summary() fonksiyonunu kullanarak da elde edebiliriz:

 summary(fit4)

Call:
lm(formula = y ~ poly(x, 4, raw = TRUE), data = df)

Residuals:
    Min 1Q Median 3Q Max 
-3.4490 -1.1732 0.6023 1.4899 3.0351 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept) -26.51615 4.94555 -5.362 0.000318 ***
poly(x, 4, raw = TRUE)1 35.82311 3.98204 8.996 4.15e-06 ***
poly(x, 4, raw = TRUE)2 -8.36486 0.96791 -8.642 5.95e-06 ***
poly(x, 4, raw = TRUE)3 0.70812 0.08954 7.908 1.30e-05 ***
poly(x, 4, raw = TRUE)4 -0.01924 0.00278 -6.922 4.08e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.424 on 10 degrees of freedom
Multiple R-squared: 0.9707, Adjusted R-squared: 0.959 
F-statistic: 82.92 on 4 and 10 DF, p-value: 1.257e-07

Eğrinin denklemi aşağıdaki gibidir:

y = -0,0192x ⁴ + 0,7081x ³ – 8,3649x ² + 35,823x – 26,516

Bu denklemi, modeldeki yordayıcı değişkenlere dayalı olarak yanıt değişkeninin değerini tahmin etmek için kullanabiliriz. Örneğin, x = 4 ise y = 23,34 olacağını tahmin ederiz:

y = -0,0192(4) ⁴ + 0,7081(4) ³ – 8,3649(4) ² + 35,823(4) – 26,516 = 23,34

Ek kaynaklar

Polinom Regresyona Giriş
R’de Polinom Regresyon (Adım Adım)
R’de seq işlevi nasıl kullanılır?