R'de öğrencileştirilmiş artıklar nasıl hesaplanır

Öğrenci kalıntısı, basitçe, tahmini standart sapmasına bölünen bir kalıntıdır.

Uygulamada genellikle, öğrenci kalıntısı 3’ün mutlak değerinden büyük olan bir veri setindeki herhangi bir gözlemin aykırı değer olduğunu söyleriz.

Aşağıdaki sözdizimini kullanan MASS paketindeki studres() işlevini kullanarak R’deki herhangi bir regresyon modelinin öğrencileştirilmiş artıklarını hızlı bir şekilde elde edebiliriz:

çiviler(model)

burada model herhangi bir doğrusal modeli temsil eder.

Örnek: R’de öğrencileştirilmiş artıkların hesaplanması

Yerleşik mtcars veri kümesini kullanarak R’de aşağıdaki basit doğrusal regresyon modelini oluşturduğumuzu varsayalım:

 #build simple linear regression model
model <- lm(mpg ~ disp, data=mtcars)

Veri kümesindeki her gözlem için öğrencileştirilmiş artıkları hesaplamak amacıyla MASS paketindeki studres() fonksiyonunu kullanabiliriz:

 library (MASS)

#calculate studentized residuals
stud_resids <- studres(model)

#view first three studentized residuals
head(stud_resids, 3)

    Mazda RX4 Mazda RX4 Wag Datsun 710 
   -0.6236250 -0.6236250 -0.7405315 

Ayrıca, yordayıcı değişkenlerin değerlerinin, üzerinde çalışılan karşılık gelen artıklara karşı hızlı bir grafiğini de oluşturabiliriz:

 #plot predictor variable vs. studentized residuals
plot(mtcars$disp, stud_resids, ylab=' Studentized Residuals ', xlab=' Displacement ') 

#add horizontal line at 0
abline(0, 0) 

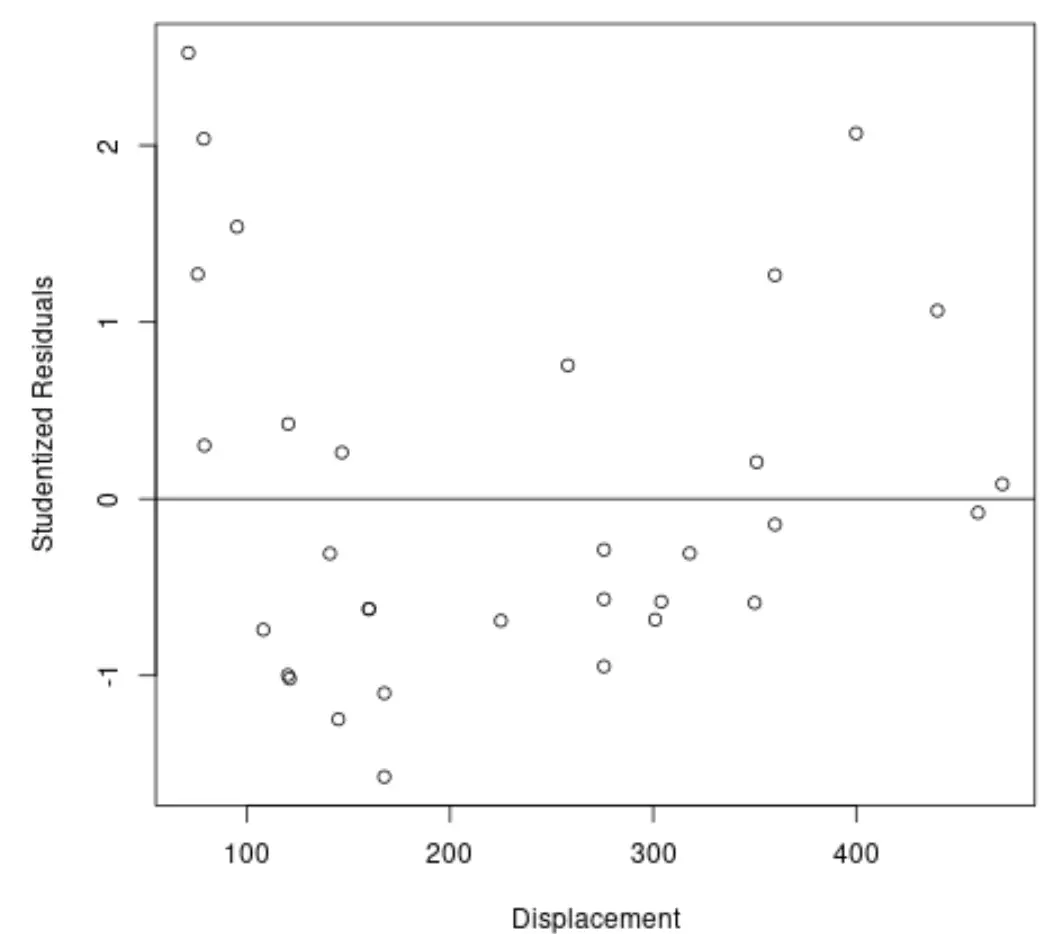
Grafikten, hiçbir gözlemin mutlak değeri 3’ten büyük olan bir öğrenci kalıntısına sahip olmadığını görebiliriz, dolayısıyla veri setinde net aykırı değerler yoktur.

İsterseniz orijinal veri setindeki her gözlemin öğrencileştirilmiş kalıntılarını da geri ekleyebiliriz:

 #add studentized residuals to orignal dataset
final_data <- cbind (mtcars[c(' mpg ', ' disp ')], stud_resids)

#view final dataset
head(final_data)

                   mpg disp stud_resids
Mazda RX4 21.0 160 -0.6236250
Mazda RX4 Wag 21.0 160 -0.6236250
Datsun 710 22.8 108 -0.7405315
Hornet 4 Drive 21.4 258 0.7556078
Hornet Sportabout 18.7 360 1.2658336
Valiant 18.1 225 -0.6896297

Daha sonra hangi gözlemlerin aykırı değerlere en yakın olduğu hakkında bir fikir edinmek için her gözlemi öğrenci kalıntısına göre en büyükten en küçüğe doğru sıralayabiliriz:

 #sort studentized residuals descending
final_data[ order (-stud_resids),]

                     mpg disp stud_resids
Toyota Corolla 33.9 71.1 2.52397102
Pontiac Firebird 19.2 400.0 2.06825391
Fiat 128 32.4 78.7 2.03684699
Lotus Europa 30.4 95.1 1.53905536
Honda Civic 30.4 75.7 1.27099586
Hornet Sportabout 18.7 360.0 1.26583364
Chrysler Imperial 14.7 440.0 1.06486066
Hornet 4 Drive 21.4 258.0 0.75560776
Porsche 914-2 26.0 120.3 0.42424678
Fiat X1-9 27.3 79.0 0.30183728
Merc 240D 24.4 146.7 0.26235893
Ford Pantera L 15.8 351.0 0.20825609
Cadillac Fleetwood 10.4 472.0 0.08338531
Lincoln Continental 10.4 460.0 -0.07863385
Duster 360 14.3 360.0 -0.14476167
Merc 450SL 17.3 275.8 -0.28759769
Dodge Challenger 15.5 318.0 -0.30826585
Merc 230 22.8 140.8 -0.30945955
Merc 450SE 16.4 275.8 -0.56742476
AMC Javelin 15.2 304.0 -0.58138205
Camaro Z28 13.3 350.0 -0.58848471
Mazda RX4 Wag 21.0 160.0 -0.62362497
Mazda RX4 21.0 160.0 -0.62362497
Maserati Bora 15.0 301.0 -0.68315010
Valiant 18.1 225.0 -0.68962974
Datsun 710 22.8 108.0 -0.74053152
Merc 450SLC 15.2 275.8 -0.94814699
Toyota Corona 21.5 120.1 -0.99751166
Volvo 142E 21.4 121.0 -1.01790487
Merc 280 19.2 167.6 -1.09979261
Ferrari Dino 19.7 145.0 -1.24732999
Merc 280C 17.8 167.6 -1.57258064

Ek kaynaklar

R’de basit doğrusal regresyon nasıl gerçekleştirilir
R’de çoklu doğrusal regresyon nasıl gerçekleştirilir
R’de artık arsa nasıl oluşturulur