Rastgele değişkenler nelerdir?

Genellikle X ile gösterilen rastgele değişken , olası değerleri rastgele bir sürecin sonuçları olan bir değişkendir.

İki tür rastgele değişken vardır: kesikli ve sürekli .

Ayrık rastgele değişkenler

Ayrık bir rastgele değişken, yalnızca 0, 1, 2, 3, 4, 5…100, 1 milyon vb. gibi sayılabilir sayıda farklı değer alabilen bir değişkendir. Ayrık rastgele değişkenlere bazı örnekler:

• Bir paranın 20 kez atılmasından sonra yazı gelme sayısı.
• Bir zarın 100 kez atıldıktan sonra 4 rakamına gelme sayısı.
• 50 widget’lık bir kutudaki kusurlu widget’ların sayısı.

Ayrık bir rastgele değişken için olasılık dağılımı, bize rastgele değişkenin belirli değerleri alma olasılığını söyler.

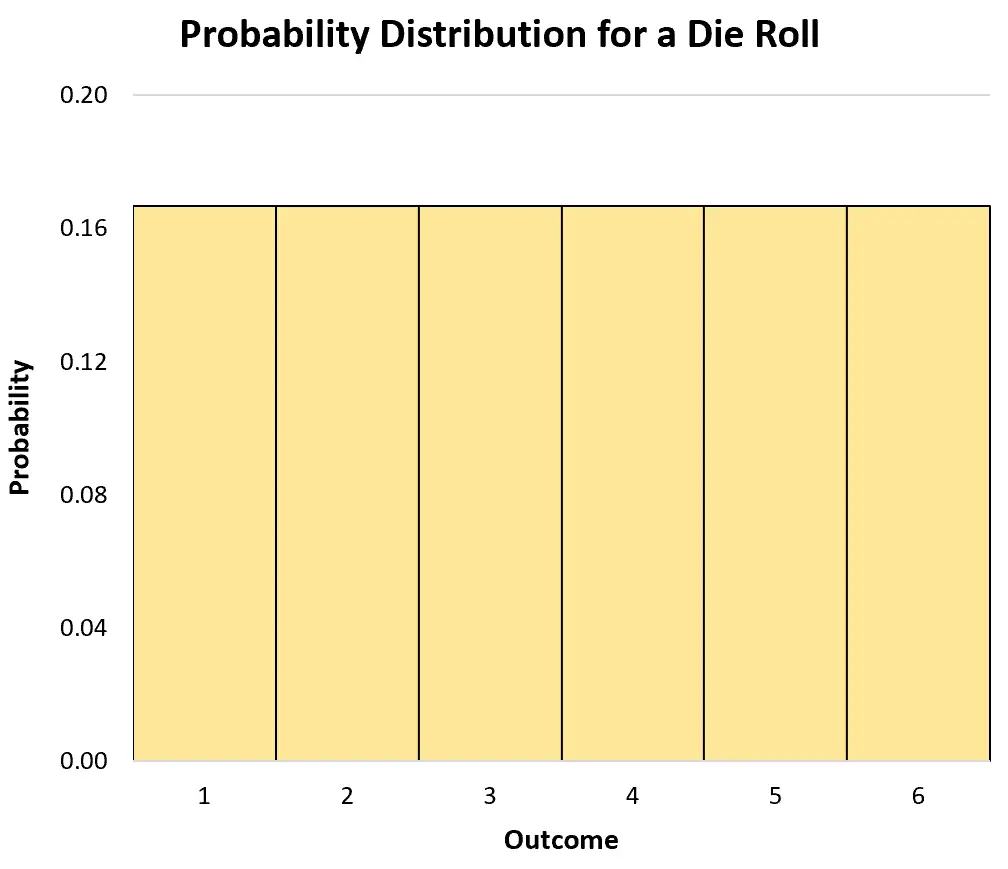
Örneğin adil bir zarı bir kez attığımızı varsayalım. X’in zarın belirli bir sayıya düşme olasılığını göstermesine izin verirsek olasılık dağılımı şu şekilde yazılabilir:

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

Not:

Bir olasılık dağılımının geçerli olabilmesi için aşağıdaki iki kriteri karşılaması gerekir:

1. Her sonucun olasılığı 0 ile 1 arasında olmalıdır.

2. Tüm olasılıkların toplamı 1 olmalıdır.

Kalıp rulosunun olasılık dağılımının bu kriterlerin her ikisini de karşıladığını unutmayın:

1. Her sonucun olasılığı 0 ile 1 arasındadır.

2. Tüm olasılıkların toplamı 1’e eşittir.

Olasılık dağılımını görselleştirmek için bir histogram kullanabiliriz:

Ayrık bir rastgele değişken için kümülatif olasılık dağılımı, bize değişkenin belirli bir değere eşit veya daha düşük bir değer alma olasılığını söyler.

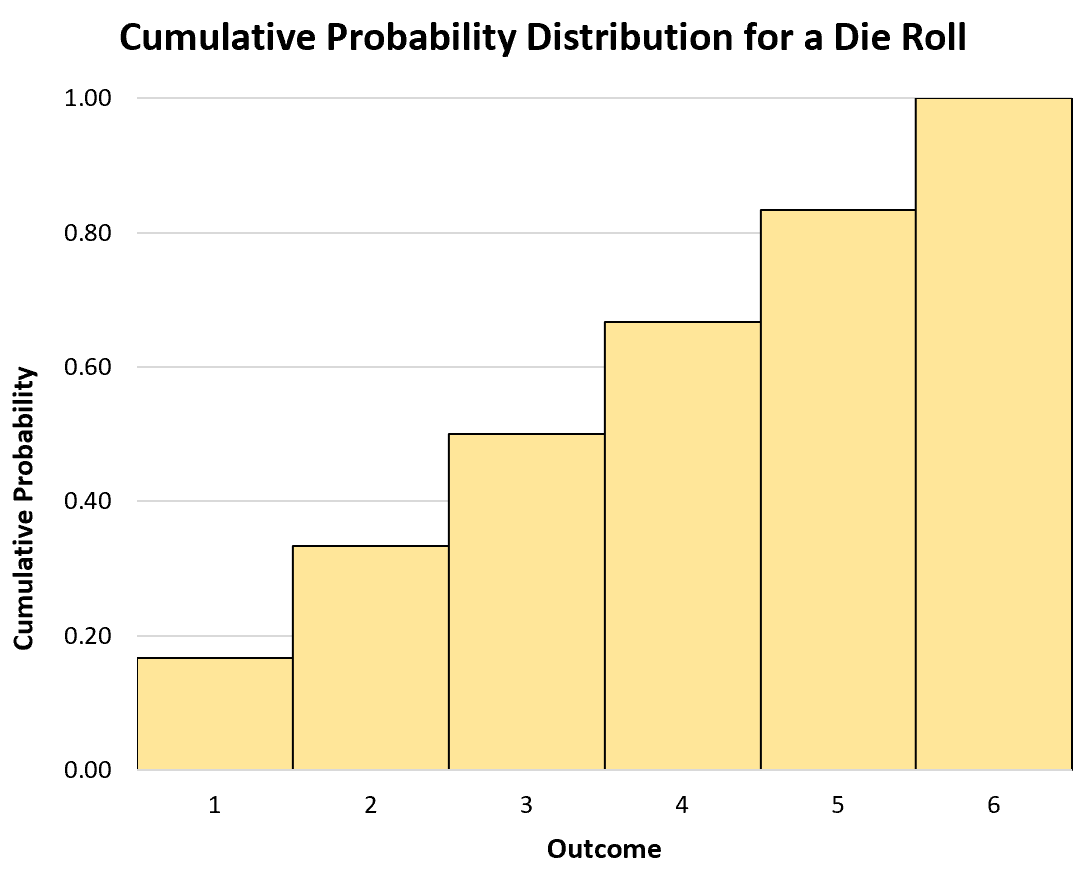
Örneğin, bir zar atışının kümülatif olasılık dağılımı şöyle görünecektir:

• P(X≤1): 1/6
• P(X≤2): 2/6
• P(X≤3): 3/6
• P(X≤4): 4/6
• P(X≤5): 5/6
• P(X≤6): 6/6

Zarın bir veya daha az sayıya gelme şansı 1/6’dır, çünkü birden daha küçük bir sayıya düşemez.

İki veya daha az yere düşme olasılığı P(X=1) + P(X=2) = 1/6 + 1/6 = 2/6’dır.

Benzer şekilde, üç veya daha az yere düşme olasılığı P(X=1) + P(X=2) + P(X=3) = 1/6 + 1/6 + 1/6 = 3/6 , Ve yakında.

Kümülatif olasılık dağılımını görselleştirmek için bir histogram da kullanabiliriz:

Sürekli rastgele değişkenler

Sürekli rastgele değişken, sonsuz sayıda olası değer alabilen bir değişkendir. Sürekli rastgele değişkenlere bazı örnekler:

• Bir hayvanın ağırlığı
• Bir kişinin yüksekliği
• Maraton koşmak için gereken süre

Örneğin, bir kişinin boyu 60,2 inç, 65,2344 inç, 70,431222 inç vb. olabilir. Boyut için sonsuz sayıda olası değer vardır.

Genel kural:

Sonuçların sayısını sayabiliyorsanız , ayrı bir rastgele değişkenle çalışıyorsunuz demektir; örneğin, bir madalyonun kaç kez tura geldiğini saymak gibi.

Ancak sonucu ölçebiliyorsanız , sürekli bir rastgele değişkenle çalışıyorsunuz demektir; örneğin boy, kilo, zaman vb. ölçümü.

Sürekli bir rastgele değişken için olasılık dağılımı, bize rastgele değişkenin belirli değerleri alma olasılığını anlatır.

Bununla birlikte, ayrık rastgele değişkenlere yönelik olasılık dağılımından farklı olarak, sürekli bir rastgele değişkene yönelik olasılık dağılımı, yalnızca değişkenin bir değer aralığını alma olasılığını bize bildirmek için kullanılabilir.

Örneğin, belirli bir restorandaki hamburgerin çeyrek pound (0,25 pound) ağırlığında olma olasılığını bilmek istediğimizi varsayalım. Ağırlık sürekli bir değişken olduğundan sonsuz sayıda değer alabilir.

Örneğin, belirli bir hamburgerin ağırlığı aslında 0,250001 pound, 0,24 pound veya 0,2488 pound olabilir. Belirli bir hamburgerin tam olarak 0,25 pound ağırlığında olma olasılığı aslında sıfırdır.

Dolayısıyla bir hamburgerin ağırlığının 0,25 lbs’den az, 0,25 lbs’den fazla veya belirli bir aralıkta (örneğin 0,23 lbs ile 0,27 lbs arasında) olma olasılığını bize bildirmek için olasılık dağılımını kullanabiliriz.

Ek kaynaklar

Aşağıdaki eğitimler rastgele değişkenler hakkında ek bilgi sağlar:

iid rastgele değişkenler nelerdir?
Gerçek hayatta rastgele değişkenlere 10 örnek