R'de çarpıklık ve basıklık nasıl hesaplanır

İstatistikte çarpıklık ve basıklık bir dağılımın şeklini ölçmenin iki yoludur.

Çarpıklık , bir dağılımın çarpıklığının bir ölçüsüdür. Bu değer pozitif ya da negatif olabilir.

• Negatif çarpıklık, kuyruğun dağılımın sol tarafında olduğunu ve daha negatif değerlere doğru uzandığını gösterir.
• Pozitif bir çarpıklık, kuyruğun dağılımın sağ tarafında olduğunu ve daha pozitif değerlere doğru uzandığını gösterir.
• Sıfır değeri, dağılımda asimetri olmadığını, yani dağılımın tamamen simetrik olduğunu gösterir.

Basıklık, bir dağılımın normal dağılıma göre ağır mı yoksa hafif kuyruklu mu olduğunun ölçüsüdür.

• Normal dağılımın basıklığı 3’tür.
• Belirli bir dağılımın basıklığı 3’ten küçükse buna playkurtic denir, bu da normal dağılıma göre giderek daha az uç değerler üretme eğiliminde olduğu anlamına gelir.
• Belirli bir dağılımın basıklığı 3’ten büyükse buna leptokurtik denir, bu da normal dağılımdan daha fazla aykırı değer üretme eğiliminde olduğu anlamına gelir.

Not: Bazı formüller (Fisher tanımı), normal dağılımla karşılaştırmayı kolaylaştırmak için basıklıktan 3 çıkarır. Bu tanımı kullanarak, basıklık değeri 0’dan büyük olan bir dağılım normal dağılıma göre daha büyük basıklığa sahip olacaktır.

Bu eğitimde, R’de belirli bir veri kümesinin hem çarpıklığının hem de basıklığının nasıl hesaplanacağı açıklanmaktadır.

Örnek: R’de Çarpıklık ve Düzleşme

Aşağıdaki veri setine sahip olduğumuzu varsayalım:

 data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)

Bu veri kümesindeki değerlerin dağılımını bir histogram oluşturarak hızlı bir şekilde görselleştirebiliriz:

 hist(data, col=' steelblue ') 

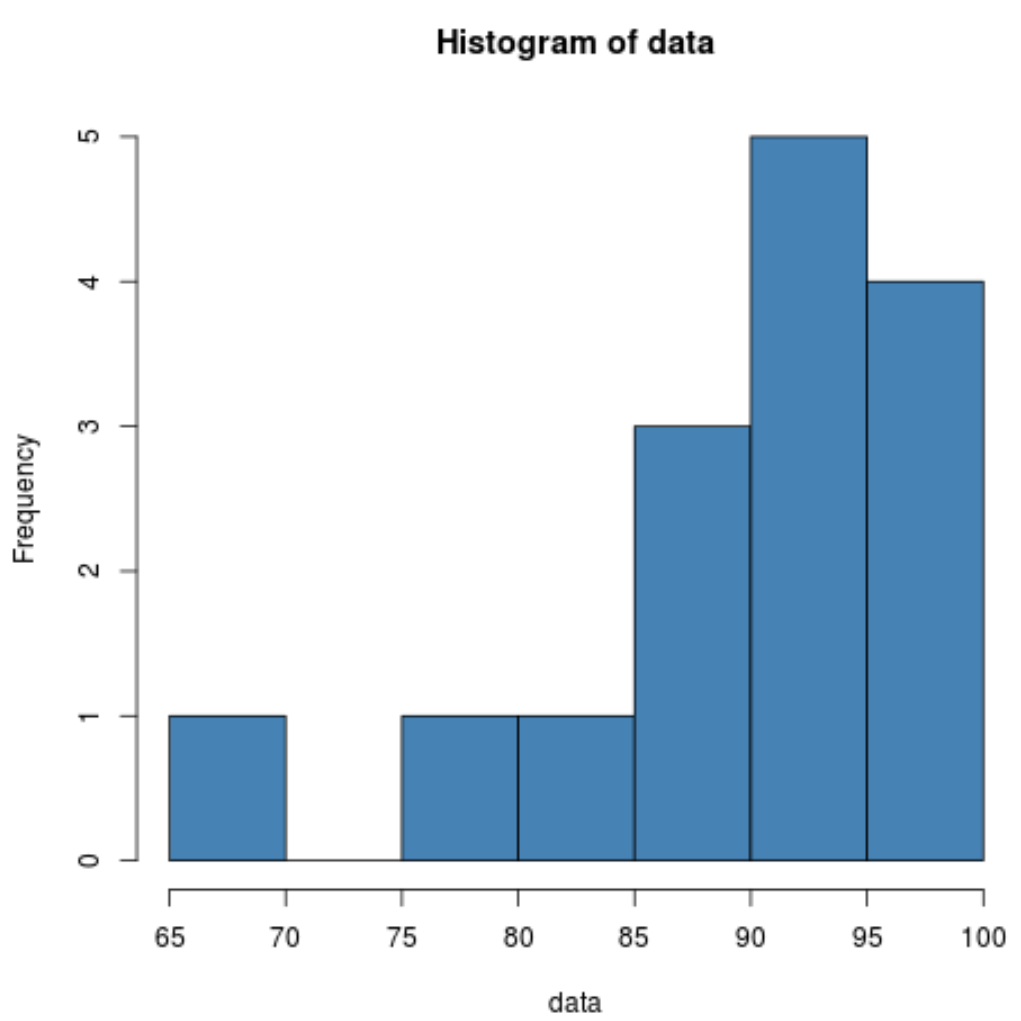
Histogram bize dağılımın sola çarpık göründüğünü gösteriyor. Yani değerlerin daha büyük bir kısmı dağılımın sağ tarafında yoğunlaşmıştır.

Bu veri kümesinin çarpıklığını ve basıklığını hesaplamak için R’deki moment kütüphanesindeki skewness() ve basıklık() işlevlerini kullanabiliriz:

 library (moments)

#calculate skewness
skewness(data)

[1] -1.391777

#calculate kurtosis
kurtosis(data)

[1] 4.177865

Çarpıklık -1,391777 ve basıklık 4,177865 olarak ortaya çıkıyor.

Çarpıklığın negatif olması dağılımın çarpık kaldığını gösterir. Bu histogramda gördüklerimizi doğruluyor.

Basıklığın 3’ten büyük olması, dağılımın normal dağılıma göre kuyruklarda daha fazla değere sahip olduğunu gösterir.

Momentler kitaplığı ayrıca, örnek verilerin normal dağılımla tutarlı çarpıklık ve basıklık gösterip göstermediğini belirleyen bir uyum iyiliği testi gerçekleştiren jarque.test() işlevini de sunar. Bu testin sıfır ve alternatif hipotezleri aşağıdaki gibidir:

Boş hipotez : Veri seti normal dağılıma karşılık gelen çarpıklık ve basıklığa sahiptir.

Alternatif hipotez : Veri kümesinde normal dağılıma uymayan çarpıklık ve basıklık var.

Aşağıdaki kod bu testin nasıl gerçekleştirileceğini gösterir:

 jarque.test(data)

	Jarque-Bera Normality Test

data:data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater

Testin p değeri 0,05756 olarak çıkıyor. Bu değer α = 0,05’ten küçük olmadığı için sıfır hipotezini reddedemiyoruz. Bu veri setinin normal dağılımdan farklı çarpıklık ve basıklığa sahip olduğunu söyleyecek yeterli kanıtımız yok.

Moments Library belgelerinin tamamını burada bulabilirsiniz.

Bonus: çarpıklık ve basıklık hesaplayıcısı

Ayrıca belirli bir veri kümesi için çarpıklığı ve basıklığı otomatik olarak hesaplayan İstatistiksel Çarpıklık ve Basıklık Hesaplayıcı’yı kullanarak belirli bir veri kümesi için çarpıklığı hesaplayabilirsiniz .