R'de basit doğrusal regresyon nasıl gerçekleştirilir (adım adım)

Basit doğrusal regresyon, tek bir açıklayıcı değişken ile tek bir yanıt değişkeni arasındaki ilişkiyi anlamak için kullanabileceğimiz bir tekniktir.

Özetle, bu teknik verilere en iyi “uyan” çizgiyi bulur ve aşağıdaki formu alır:

ŷ = b ₀ + b ₁ x

Altın:

• ŷ : Tahmini yanıt değeri
• b ₀ : Regresyon çizgisinin başlangıcı
• b ₁ : Regresyon çizgisinin eğimi

Bu denklem açıklayıcı değişken ile yanıt değişkeni arasındaki ilişkiyi anlamamıza yardımcı olabilir ve (istatistiksel olarak anlamlı olduğu varsayılarak) açıklayıcı değişkenin değeri göz önüne alındığında bir yanıt değişkeninin değerini tahmin etmek için kullanılabilir.

Bu eğitim, R’de basit doğrusal regresyonun nasıl gerçekleştirileceğine ilişkin adım adım bir açıklama sağlar.

1. Adım: Verileri yükleyin

Bu örnekte 15 öğrenci için aşağıdaki iki değişkeni içeren sahte bir veri seti oluşturacağız:

• Belirli sınavlar için çalışılan toplam saat sayısı
• Sınav sonucu

Açıklayıcı değişken olarak saatleri ve yanıt değişkeni olarak muayene sonuçlarını kullanarak basit bir doğrusal regresyon modeli uydurmaya çalışacağız.

Aşağıdaki kod, bu sahte veri kümesinin R’de nasıl oluşturulacağını gösterir:

 #create dataset
df <- data.frame(hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of dataset
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

#attach dataset to make it more convenient to work with
attach(df)

2. Adım: Verileri görselleştirin

Basit bir doğrusal regresyon modeli kurmadan önce, anlamak için öncelikle verileri görselleştirmemiz gerekir.

İlk olarak, saat ve puan arasındaki ilişkinin yaklaşık olarak doğrusal olduğundan emin olmak istiyoruz çünkü bu, basit doğrusal regresyonun temelinde yatan çok büyük bir varsayımdır. İki değişken arasındaki ilişkiyi görselleştirmek için basit bir dağılım grafiği oluşturabiliriz:

 scatter.smooth(hours, score, main=' Hours studied vs. Exam Score ')

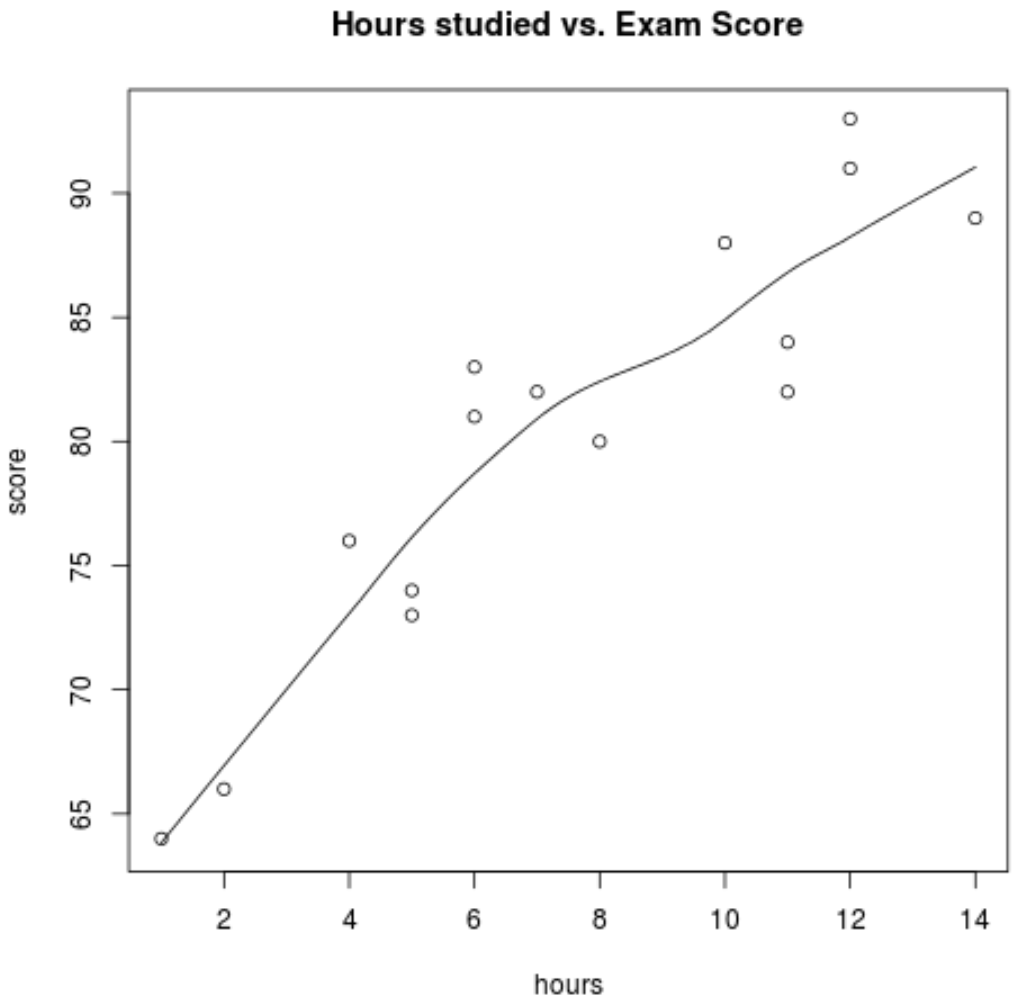
Grafikten ilişkinin doğrusal olduğunu görebiliriz. Saat sayısı arttıkça puan da doğrusal olarak artma eğilimindedir.

Daha sonra sınav sonuçlarının dağılımını görselleştirmek ve aykırı değerleri kontrol etmek için bir kutu grafiği oluşturabiliriz. Varsayılan olarak R, bir gözlemi, üçüncü çeyreğin (Q3) çeyrekler arası aralığın 1,5 katı üzerinde veya ilk çeyreğin (Q1) altındaki çeyrekler arası aralığın 1,5 katı olması durumunda aykırı değer olarak tanımlar.

Bir gözlem aykırı ise kutu grafiğinde küçük bir daire görünecektir:

 boxplot(score) 

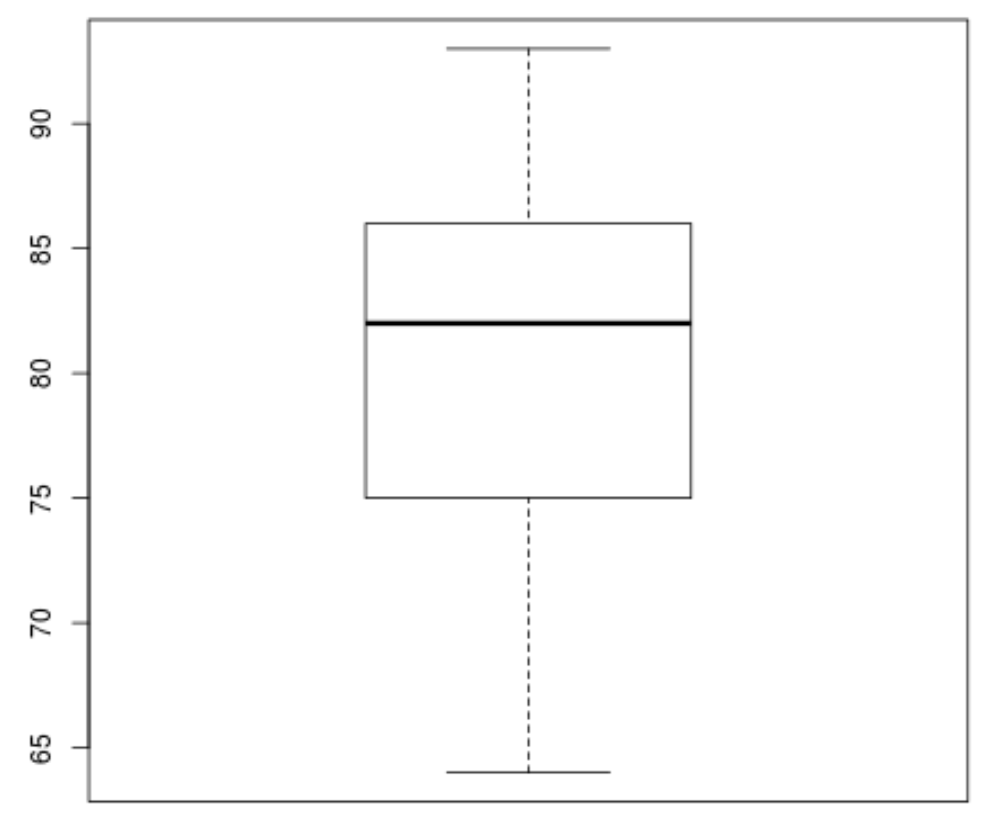
Kutu grafiğinde küçük daireler yok, bu da veri setimizde aykırı değerlerin olmadığı anlamına geliyor.

Adım 3: Basit Doğrusal Regresyon Gerçekleştirin

Değişkenlerimiz arasındaki ilişkinin doğrusal olduğunu ve aykırı değerlerin olmadığını doğruladıktan sonra, açıklayıcı değişken olarak saatleri ve yanıt değişkeni olarak puanı kullanarak basit bir doğrusal regresyon modeli uydurmaya devam edebiliriz:

 #fit simple linear regression model
model <- lm(score~hours)

#view model summary
summary(model)

Call:
lm(formula = score ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

Model özetinden uygun regresyon denkleminin şöyle olduğunu görebiliriz:

Puan = 65,334 + 1,982*(saat)

Bu, çalışılan her ek saatin ortalama 1.982 puanlık sınav puanı artışıyla ilişkili olduğu anlamına gelir. Ve 65.334’ün orijinal değeri bize sıfır saat ders çalışan bir öğrencinin ortalama beklenen sınav puanını söylüyor.

Bu denklemi, öğrencinin ders çalıştığı saat sayısına göre beklenen sınav puanını bulmak için de kullanabiliriz. Örneğin 10 saat ders çalışan bir öğrencinin sınav puanının 85,15 olması gerekir:

Puan = 65,334 + 1,982*(10) = 85,15

Model özetinin geri kalanını şu şekilde yorumlayabilirsiniz:

• Pr(>|t|): Model katsayılarıyla ilişkili p değeridir. Saatlere ilişkin p değeri (2,25e-06) 0,05’ten anlamlı derecede küçük olduğundan saat ile puan arasında istatistiksel olarak anlamlı bir ilişkinin olduğunu söyleyebiliriz.
• Çoklu R-kare: Bu sayı bize sınav puanlarındaki değişim yüzdesinin çalışılan saat sayısıyla açıklanabileceğini söyler. Genel olarak, bir regresyon modelinin R-kare değeri ne kadar büyük olursa, açıklayıcı değişkenler yanıt değişkeninin değerini o kadar iyi tahmin edebilir. Bu durumda puanlardaki değişimin %83,1’i çalışılan saatlerle açıklanabilir.
• Artık standart hata: gözlenen değerler ile regresyon çizgisi arasındaki ortalama mesafedir. Bu değer ne kadar düşük olursa, bir regresyon çizgisinin gözlemlenen verilere o kadar fazla karşılık gelebilmesi mümkündür. Bu durumda sınavda gözlemlenen ortalama puan, regresyon çizgisinin öngördüğü puandan 3.641 puan sapmaktadır.
• F istatistiği ve p değeri: F istatistiği ( 63.91 ) ve karşılık gelen p değeri ( 2.253e-06 ) bize regresyon modelinin genel önemini, yani modeldeki açıklayıcı değişkenlerin varyasyonu açıklamakta yararlı olup olmadığını anlatır. . yanıt değişkeninde. Bu örnekteki p değeri 0,05’ten küçük olduğundan modelimiz istatistiksel olarak anlamlıdır ve saatlerin puan değişimini açıklamada faydalı olduğu düşünülmektedir.

Adım 4: Artık Grafikler Oluşturun

Basit doğrusal regresyon modelini verilere yerleştirdikten sonra son adım, artık grafiklerin oluşturulmasıdır.

Doğrusal regresyonun temel varsayımlarından biri, bir regresyon modelinin artıklarının yaklaşık olarak normal dağıldığı ve açıklayıcı değişkenin her seviyesinde homoskedastik olduğudur. Bu varsayımların karşılanmaması halinde regresyon modelimizin sonuçları yanıltıcı veya güvenilmez olabilir.

Bu varsayımların karşılandığını doğrulamak için aşağıdaki kalan grafikleri oluşturabiliriz:

Artıkların ve uydurulmuş değerlerin grafiği: Bu grafik, eş varyanslılığın doğrulanması için kullanışlıdır. X ekseni takılan değerleri, y ekseni ise artıkları görüntüler. Artıklar grafik boyunca sıfır değeri etrafında rastgele ve düzgün bir şekilde dağılmış göründüğü sürece, eş varyanslılığın ihlal edilmediğini varsayabiliriz:

 #define residuals
res <- resid(model)

#produce residual vs. fitted plot
plot(fitted(model), res)

#add a horizontal line at 0 
abline(0,0)

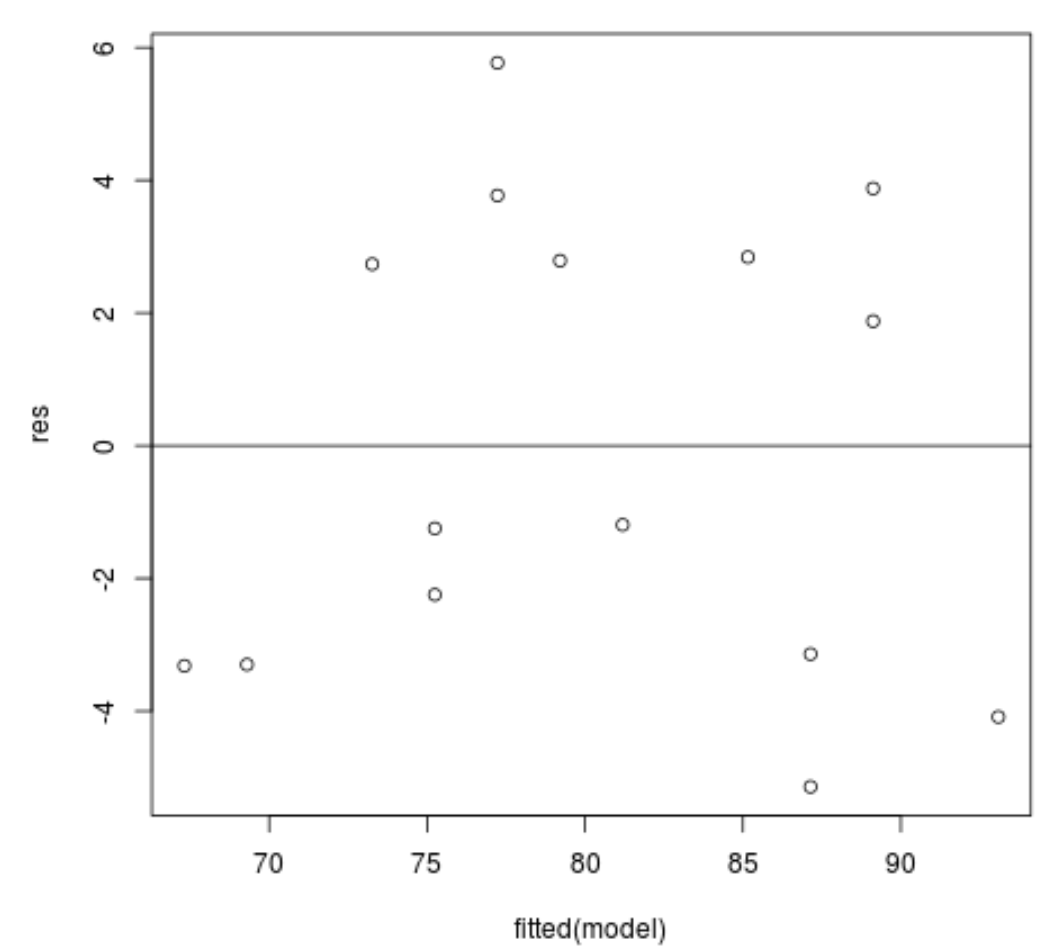
Artıklar sıfır etrafında rastgele dağılmış gibi görünüyor ve fark edilebilir bir desen göstermiyor, dolayısıyla bu varsayım karşılanıyor.

QQ grafiği: Bu grafik, artıkların normal bir dağılım takip edip etmediğini belirlemek için kullanışlıdır. Çizimdeki veri değerleri 45 derecelik açıyla kabaca düz bir çizgi izliyorsa veriler normal şekilde dağılır:

 #create QQ plot for residuals
qqnorm(res)

#add a straight diagonal line to the plot
qqline(res) 

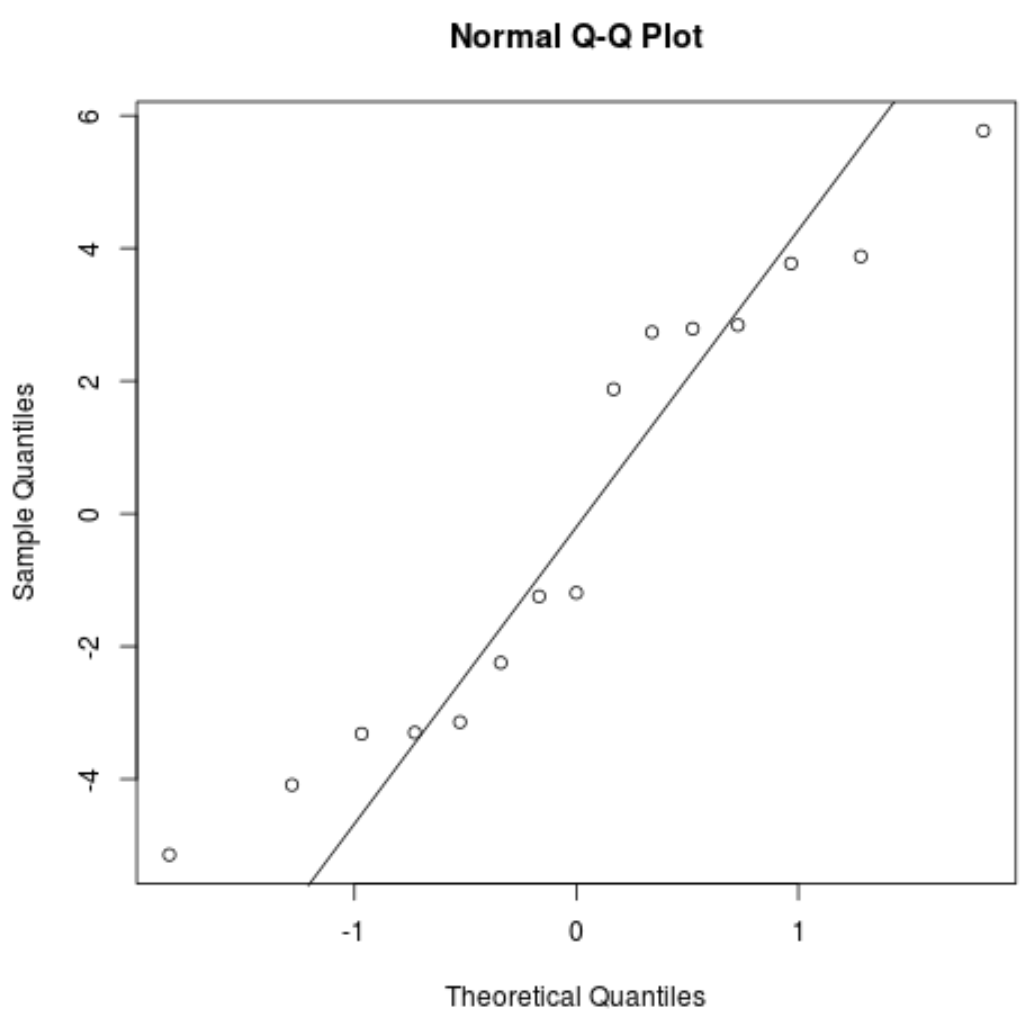
Kalıntılar 45 derece çizgisinden biraz sapıyor ancak ciddi endişe yaratacak kadar değil. Normallik varsayımının karşılandığını varsayabiliriz.

Artıklar normal dağılımlı ve homoskedastik olduğundan, basit doğrusal regresyon modelinin varsayımlarının karşılandığını doğruladık. Dolayısıyla modelimizin çıktısı güvenilirdir.

Bu eğitimde kullanılan R kodunun tamamını burada bulabilirsiniz.