R'de bonferroni düzeltmesi nasıl yapılır

Üç veya daha fazla bağımsız grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için tek yönlü ANOVA kullanılır.

ANOVA tablosunun genel p değeri belirli bir anlamlılık düzeyinin altındaysa, grup ortalamalarından en az birinin diğerlerinden farklı olduğunu söylemek için yeterli kanıtımız var demektir.

Ancak bu bize hangi grupların birbirinden farklı olduğunu söylemez. Bu bize basitçe tüm grup ortalamalarının eşit olmadığını söyler.

Hangi grupların birbirinden farklı olduğunu tam olarak bilmek için, aile bazında hata oranını kontrol ederken her grup arasında ikili t-testleri yapmamız gerekir.

Bunu başarmanın en yaygın yollarından biri, ikili t testlerinin her biri için p değerlerini hesaplarken Bonferroni düzeltmesini kullanmaktır.

Bu eğitimde R’de Bonferroni düzeltmesinin nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: R’de Bonferroni düzeltmesi

Bir öğretmenin üç farklı çalışma tekniğinin öğrenciler arasında farklı test puanlarına yol açıp açmadığını bilmek istediğini varsayalım.

Bunu test etmek için her çalışma tekniğini kullanmak üzere 10 öğrenciyi rastgele görevlendiriyor. Bir hafta kendilerine verilen çalışma tekniğini kullandıktan sonra her öğrenci aynı sınava girer.

Tek yönlü bir ANOVA’yı sığdırmak için R’de aşağıdaki adımları kullanabiliriz ve her grubun sınav sonuçları arasındaki ikili farkları hesaplamak için Bonferroni düzeltmesini kullanabiliriz.

Adım 1: Veri kümesini oluşturun.

Aşağıdaki kod, 30 öğrencinin tamamının sınav sonuçlarını içeren bir veri kümesinin nasıl oluşturulacağını gösterir:

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

Adım 2: Her grubun sınav sonuçlarını görüntüleyin.

Aşağıdaki kod, her grup için sınav sonuçlarının dağılımını görselleştirmek amacıyla kutu grafiklerinin nasıl oluşturulacağını gösterir:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

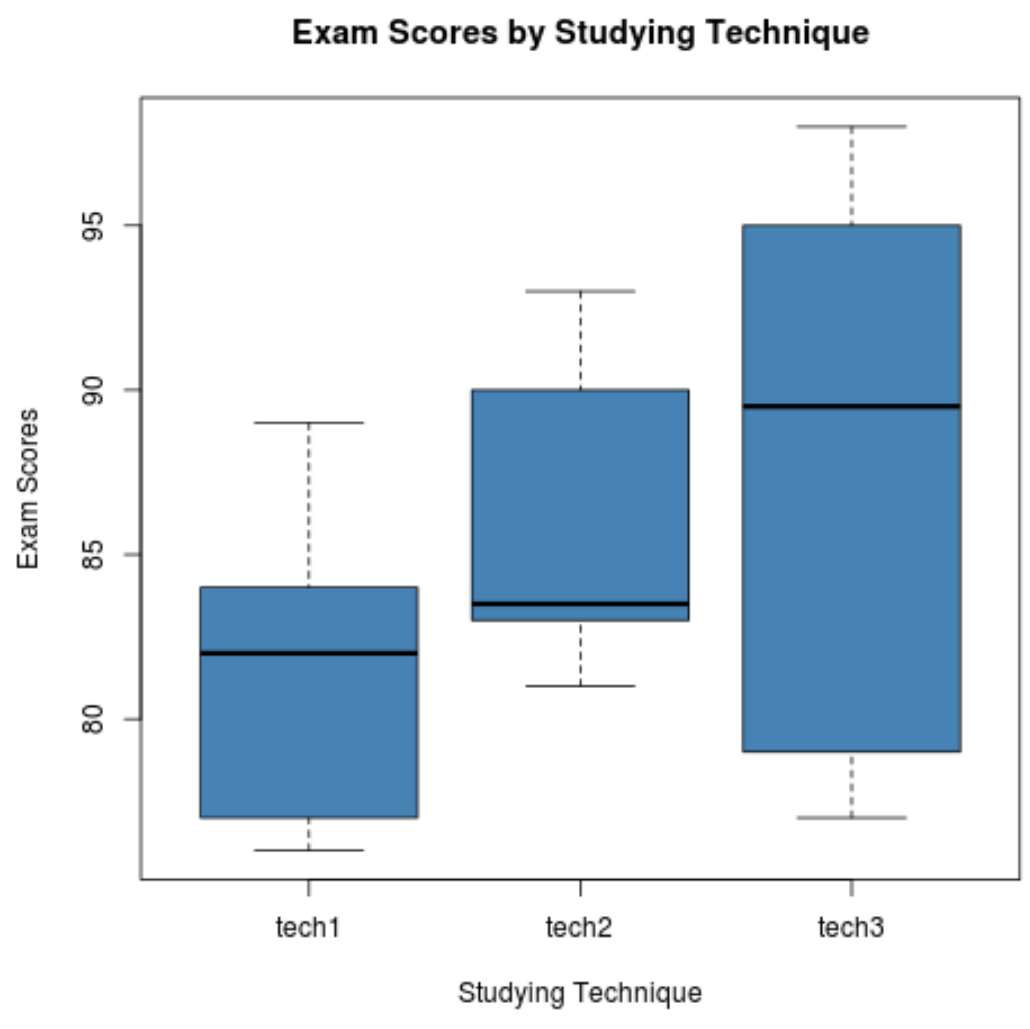
Adım 3: Tek yönlü ANOVA gerçekleştirin.

Aşağıdaki kod, her gruptaki ortalama sınav puanları arasındaki farkları test etmek için tek yönlü ANOVA’nın nasıl gerçekleştirileceğini gösterir:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Genel p değeri ( 0,0476 ) 0,05’ten küçük olduğundan bu durum her grubun aynı ortalama sınav puanına sahip olmadığını gösterir.

Daha sonra, her grubun sınav sonuçları arasındaki ikili farkları hesaplamak için p değerleri için Bonferroni düzeltmesini kullanarak ikili t testleri gerçekleştireceğiz.

Adım 4: İkili t-testlerini gerçekleştirin.

R’de Bonferroni düzeltmesi ile ikili t testleri gerçekleştirmek için aşağıdaki sözdizimini kullanan çift yönlü.t.test() işlevini kullanabiliriz:

pairwise.t.test(x, g, p.adjust.method=”bonferroni”)

Altın:

• x: yanıt değerlerinin sayısal bir vektörü
• g: Grupların adlarını belirten bir vektör (örn. çalışma tekniği)

Aşağıdaki kod, örneğimiz için bu işlevin nasıl kullanılacağını gösterir:

 #perform pairwise t-tests with Bonferroni's correction
pairwise.t.test(data$score, data$technique, p.adjust.method=" bonferroni ")

	Pairwise comparisons using t tests with pooled SD 

data: data$score and data$technique 

      tech1 tech2
tech2 0.309 -    
tech3 0.048 1.000

P value adjustment method: bonferroni

Sonucun yorumlanma şekli şu şekildedir:

• Teknik 1 ve Teknik 2 arasındaki sınav puanları arasındaki ortalama fark için düzeltilmiş p değeri 0,309’dur .
• Teknik 1 ve Teknik 3 arasındaki sınav puanları arasındaki ortalama fark için düzeltilmiş p değeri 0,048’dir .
• Teknik 2 ve Teknik 3 arasındaki sınav puanları arasındaki ortalama fark için düzeltilmiş p değeri 1000’dir .

Sonuçlara göre tek anlamlı farkın teknik 1 ile teknik 3 arasında olduğunu görebiliriz.

Ek kaynaklar

Tek Yönlü ANOVA’ya Giriş
R’de tek yönlü ANOVA nasıl gerçekleştirilir
R’de Tukey testi nasıl yapılır?
R’de Dunnett testi nasıl yapılır