R'de chow testi nasıl yapılır

İki farklı regresyon modelinin farklı veri setleri üzerindeki katsayılarının eşit olup olmadığını test etmek için Chow testi kullanılır.

Bu test tipik olarak ekonometri alanında zaman serisi verileriyle belirli bir zamanda verilerde yapısal bir kırılma olup olmadığını belirlemek için kullanılır.

Bu eğitimde R’de Chow testinin nasıl gerçekleştirileceğine ilişkin adım adım bir örnek sunulmaktadır.

1. Adım: Verileri oluşturun

İlk önce sahte veriler oluşturacağız:

 #create data
data <- data.frame(x = c(1, 1, 2, 3, 4, 4, 5, 5, 6, 7, 7, 8, 8, 9, 10, 10,
                         11, 12, 12, 13, 14, 15, 15, 16, 17, 18, 18, 19, 20, 20),
                   y = c(3, 5, 6, 10, 13, 15, 17, 14, 20, 23, 25, 27, 30, 30, 31,
                         33, 32, 32, 30, 32, 34, 34, 37, 35, 34, 36, 34, 37, 38, 36))

#view first six rows of data
head(data)

  xy
1 1 3
2 1 5
3 2 6
4 3 10
5 4 13
6 4 15

2. Adım: Verileri görselleştirin

Daha sonra verileri görselleştirmek için basit bir dağılım grafiği oluşturacağız:

 #load ggplot2 visualization package
library (ggplot2)

#create scatterplot
ggplot(data, aes (x = x, y = y)) +
    geom_point(col=' steelblue ', size= 3 )

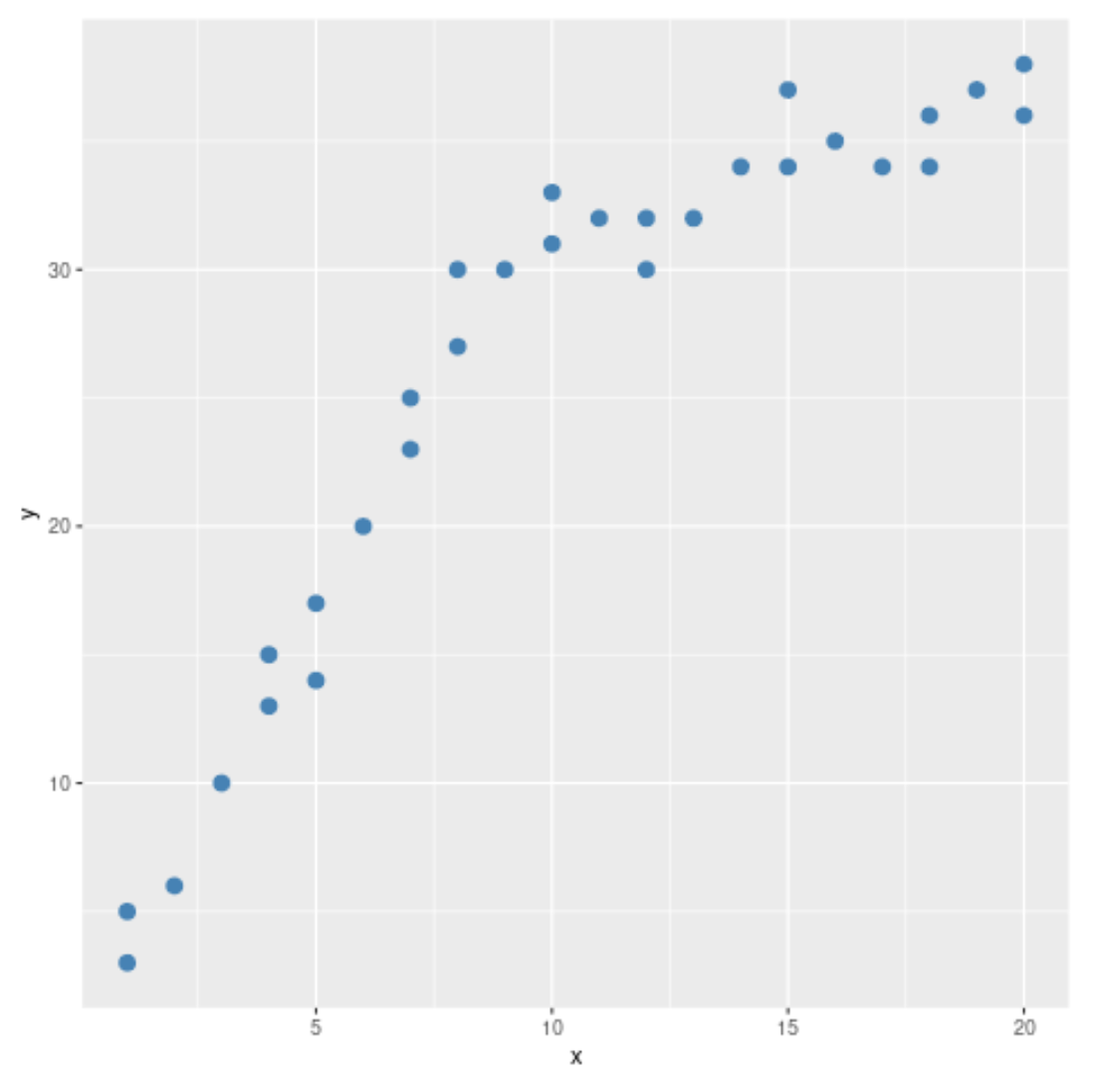
Dağılım grafiğinden verideki örüntünün x = 10’da değiştiğini görebiliriz. Böylece x = 10’da veride yapısal bir kırılma noktası olup olmadığını belirlemek için Chow testini yapabiliriz.

Adım 3: Chow Testini Gerçekleştirin

Chow testi gerçekleştirmek için strucchange paketindeki sctest fonksiyonunu kullanabiliriz :

 #load strucchange package
library (strucchange)

#perform Chow test
sctest(data$y ~ data$x, type = " Chow ", point = 10 )

	Chow test

data: data$y ~ data$x
F = 110.14, p-value = 2.023e-13

Test sonucundan şunları görebiliriz:

• F-testi istatistiği : 110.14
• p-değeri: <.0000

P değeri 0,05’ten küçük olduğundan testin sıfır hipotezini reddedebiliriz. Bu, verilerde yapısal bir kırılma noktasının mevcut olduğunu söylemek için yeterli kanıtımız olduğu anlamına gelir.

Başka bir deyişle, iki regresyon çizgisi, modeli verilere tek bir regresyon çizgisine göre daha etkili bir şekilde sığdırabilir.