R'de çok değişkenli uyarlanabilir regresyon spline'ları

Çok değişkenli uyarlamalı regresyon eğrileri (MARS), bir dizi öngörücü değişken ile bir yanıt değişkeni arasındaki doğrusal olmayan ilişkileri modellemek için kullanılabilir.

Bu yöntem şu şekilde çalışır:

1. Bir veri kümesini k parçaya bölün.

2. Her parçaya bir regresyon modeli yerleştirin.

3. k için bir değer seçmek üzere k-katlı çapraz doğrulamayı kullanın.

Bu eğitimde, bir MARS modelinin R’deki bir veri kümesine nasıl sığdırılacağına ilişkin adım adım bir örnek sağlanmaktadır.

Adım 1: Gerekli paketleri yükleyin

Bu örnek için ISLR Ücret veri kümesini kullanacağız .   3.000 kişinin yıllık maaşının yanı sıra yaş, eğitim, ırk gibi çeşitli belirleyici değişkenleri içeren paket.

Verilere bir MARS modeli yerleştirmeden önce gerekli paketleri yükleyeceğiz:

 library (ISLR) #contains Wage dataset
library (dplyr) #data wrangling
library (ggplot2) #plotting
library (earth) #fitting MARS models
library (caret) #tuning model parameters

2. Adım: Verileri görüntüleyin

Daha sonra, üzerinde çalıştığımız veri kümesinin ilk altı satırını görüntüleyeceğiz:

 #view first six rows of data
head (Wage)

       year age maritl race education region
231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic
86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic
161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic
155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic
11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic
376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic
             jobclass health health_ins logwage wage
231655 1. Industrial 1. <=Good 2. No 4.318063 75.04315
86582 2. Information 2. >=Very Good 2. No 4.255273 70.47602
161300 1. Industrial 1. <=Good 1. Yes 4.875061 130.98218
155159 2. Information 2. >=Very Good 1. Yes 5.041393 154.68529
11443 2. Information 1. <=Good 1. Yes 4.318063 75.04315
376662 2. Information 2. >=Very Good 1. Yes 4.845098 127.11574

3. Adım: MARS modelini oluşturun ve optimize edin

Daha sonra, bu veri kümesi için MARS modelini oluşturacağız ve hangi modelin en düşük test RMSE’sini (ortalama kare hatası) ürettiğini belirlemek için k-katlı çapraz doğrulama gerçekleştireceğiz.

 #create a tuning grid
hyper_grid <- expand. grid (degree = 1:3,
                          nprune = seq (2, 50, length.out = 10) %>%
floor ())

#make this example reproducible
set.seed(1)

#fit MARS model using k-fold cross-validation
cv_mars <- train(
  x = subset(Wage, select = -c(wage, logwage)),
  y = Wage$wage,
  method = " earth ",
  metric = " RMSE ",
  trControl = trainControl(method = " cv ", number = 10),
  tuneGrid = hyper_grid)

#display model with lowest test RMSE
cv_mars$results %>%
  filter (nprune==cv_mars$bestTune$nprune, degree =cv_mars$bestTune$degree)    
degree nprune RMSE Rsquared MAE RMSESD RsquaredSD MAESD		
1 12 33.8164 0.3431804 22.97108 2.240394 0.03064269 1.4554

Sonuçlardan, en düşük test MSE’sini üreten modelin yalnızca birinci dereceden etkilere (yani etkileşim terimleri olmayan) ve 12 terime sahip bir model olduğunu görebiliriz. Bu model 33,8164’lük ortalama karekök hata (RMSE) üretti.

Not: MARS modelini belirtmek için method=”earth” kullandık. Bu yönteme ilişkin belgeleri burada bulabilirsiniz.

Dereceye ve terim sayısına göre RMSE testini görselleştirmek için bir grafik de oluşturabiliriz:

 #display test RMSE by terms and degree
ggplot(cv_mars)

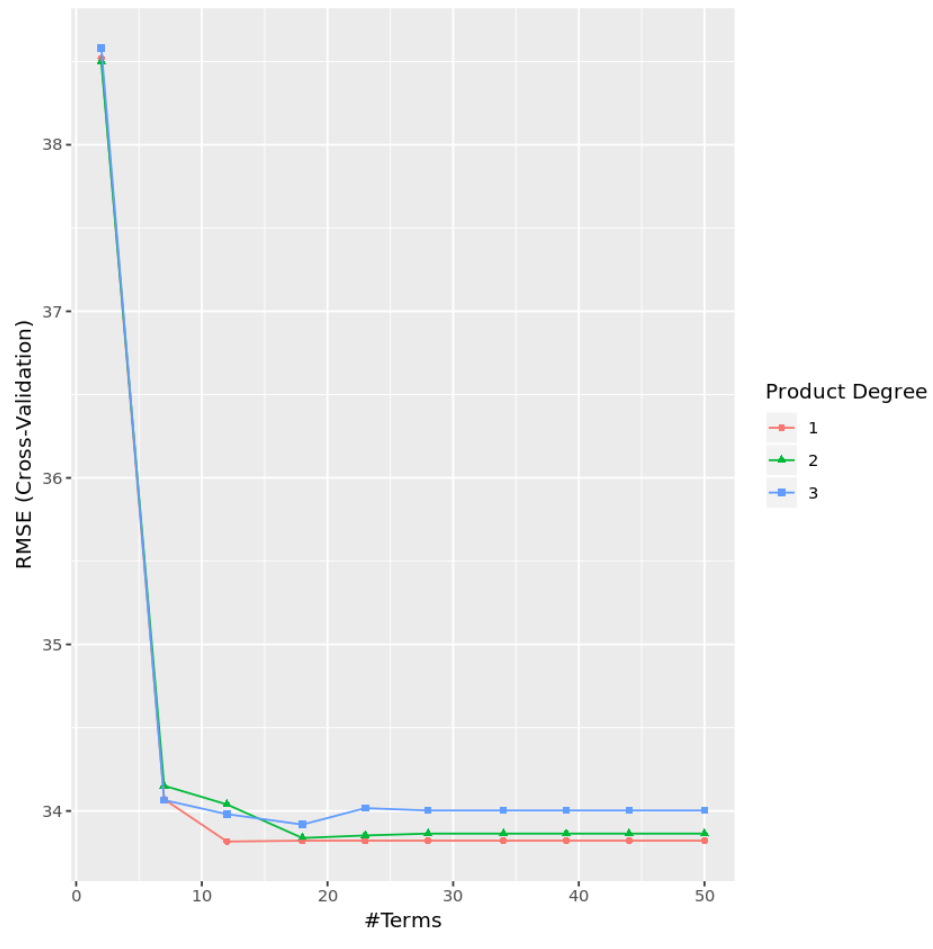
Uygulamada, bir MARS modelini aşağıdaki gibi diğer model türleriyle uyarlayacağız:

• Çoklu doğrusal gerileme
• Polinom regresyon
• Zirve regresyonu
• Kement regresyonu
• Temel bileşenler regresyonu
• Kısmi en küçük kareler

Daha sonra hangisinin en düşük test hatasına yol açtığını belirlemek için her modeli karşılaştırır ve kullanılacak en uygun model olarak bu modeli seçerdik.

Bu örnekte kullanılan R kodunun tamamını burada bulabilirsiniz.