R'de çoklu doğrusal regresyon sonuçları nasıl çizilir

R’de basit doğrusal regresyon uyguladığımızda, uygun regresyon çizgisini görselleştirmek kolaydır çünkü yalnızca tek bir tahmin değişkeni ve tek bir yanıt değişkeni ile çalışıyoruz.

Örneğin, aşağıdaki kod basit bir doğrusal regresyon modelinin bir veri kümesine nasıl sığdırılacağını ve sonuçların grafiğinin nasıl çizileceğini gösterir:

 #create dataset
data <- data.frame(x = c(1, 1, 2, 4, 4, 5, 6, 7, 7, 8, 9, 10, 11, 11),
                   y = c(13, 14, 17, 23, 24, 25, 25, 24, 28, 32, 33, 35, 40, 41))

#fit simple linear regression model
model <- lm(y ~ x, data = data)

#create scatterplot of data
plot(data$x, data$y)

#add fitted regression line
abline(model)

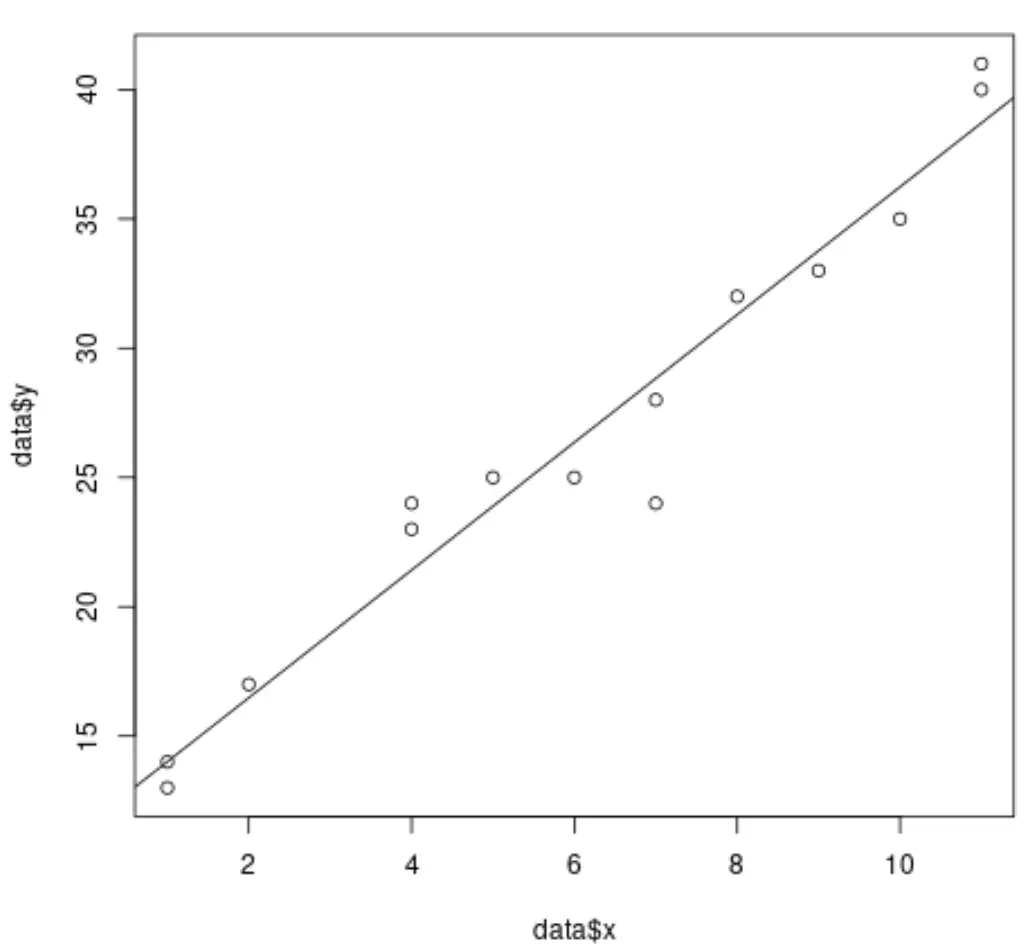
Ancak çoklu doğrusal regresyon uyguladığımızda sonuçları görselleştirmek zorlaşır çünkü birden fazla tahmin değişkeni vardır ve 2 boyutlu bir grafik üzerinde basitçe bir regresyon çizgisi çizemeyiz.

Bunun yerine, modeldeki diğer öngörücü değişkenlerin varlığını kontrol ederken yanıt değişkeni ile bir yordayıcı değişken arasındaki ilişkiyi görüntüleyen ayrı grafikler olan eklenen değişken grafiklerini (bazen “kısmi regresyon grafikleri” olarak da adlandırılır) kullanabiliriz.

Aşağıdaki örnek, R’de çoklu doğrusal regresyonun nasıl gerçekleştirileceğini ve eklenen değişken grafiklerini kullanarak sonuçların nasıl görselleştirileceğini gösterir.

Örnek: R’de Çoklu Doğrusal Regresyon Sonuçlarının Grafiği

Yerleşik mtcars veri kümesini kullanarak aşağıdaki çoklu doğrusal regresyon modelini R’deki bir veri kümesine uydurduğumuzu varsayalım:

 #fit multiple linear regression model
model <- lm(mpg ~ disp + hp + drat, data = mtcars)

#view results of model
summary(model)

Call:
lm(formula = mpg ~ disp + hp + drat, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-5.1225 -1.8454 -0.4456 1.1342 6.4958 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) 19.344293 6.370882 3.036 0.00513 **
available -0.019232 0.009371 -2.052 0.04960 * 
hp -0.031229 0.013345 -2.340 0.02663 * 
drat 2.714975 1.487366 1.825 0.07863 . 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.008 on 28 degrees of freedom
Multiple R-squared: 0.775, Adjusted R-squared: 0.7509 
F-statistic: 32.15 on 3 and 28 DF, p-value: 3.28e-09

Sonuçlardan her bir katsayı için p değerinin 0,1’den küçük olduğunu görebiliriz. Basitlik açısından, yordayıcı değişkenlerin her birinin anlamlı olduğunu ve modele dahil edilmesi gerektiğini varsayacağız.

Eklenen değişkenlerin grafiklerini oluşturmak için araba paketindeki avPlots() fonksiyonunu kullanabiliriz:

 #load car package
library(car)

#produce added variable plots
avPlots(model)

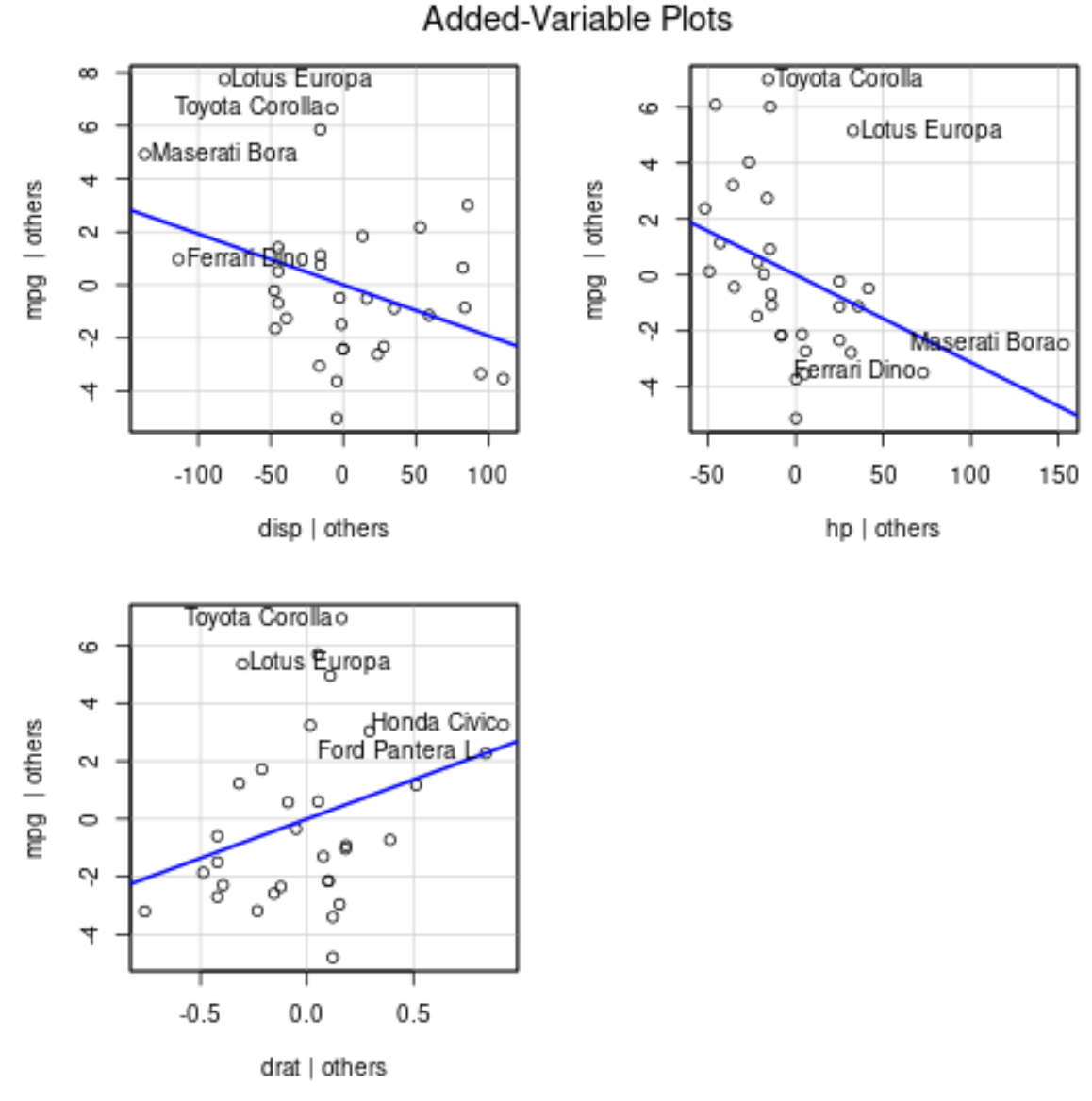
Her grafiği nasıl yorumlayacağınız aşağıda açıklanmıştır:

• X ekseni tek bir öngörücü değişkeni görüntüler ve y ekseni yanıt değişkenini görüntüler.
• Mavi çizgi , diğer tüm öngörücü değişkenlerin değerini sabit tutarken , yordayıcı değişken ile yanıt değişkeni arasındaki ilişkiyi gösterir.
• Her grafikteki etiketli noktalar, en büyük artıklara sahip 2 gözlemi ve en büyük kısmi kaldıraca sahip 2 gözlemi temsil eder.

Her grafikteki çizginin açısının, tahmin edilen regresyon denkleminin katsayısının işaretine karşılık geldiğine dikkat edin.

Örneğin, modeldeki her bir yordayıcı değişken için tahmin edilen katsayılar şunlardır:

• ekran: -0.019232
• kanal: -0.031229
• tarih: 2.714975

Drat için eklenen değişken grafiğinde çizginin açısının pozitif olduğunu, disp ve hp için ise negatif olduğunu ve bunların tahmini katsayılarının işaretlerine karşılık geldiğini unutmayın:

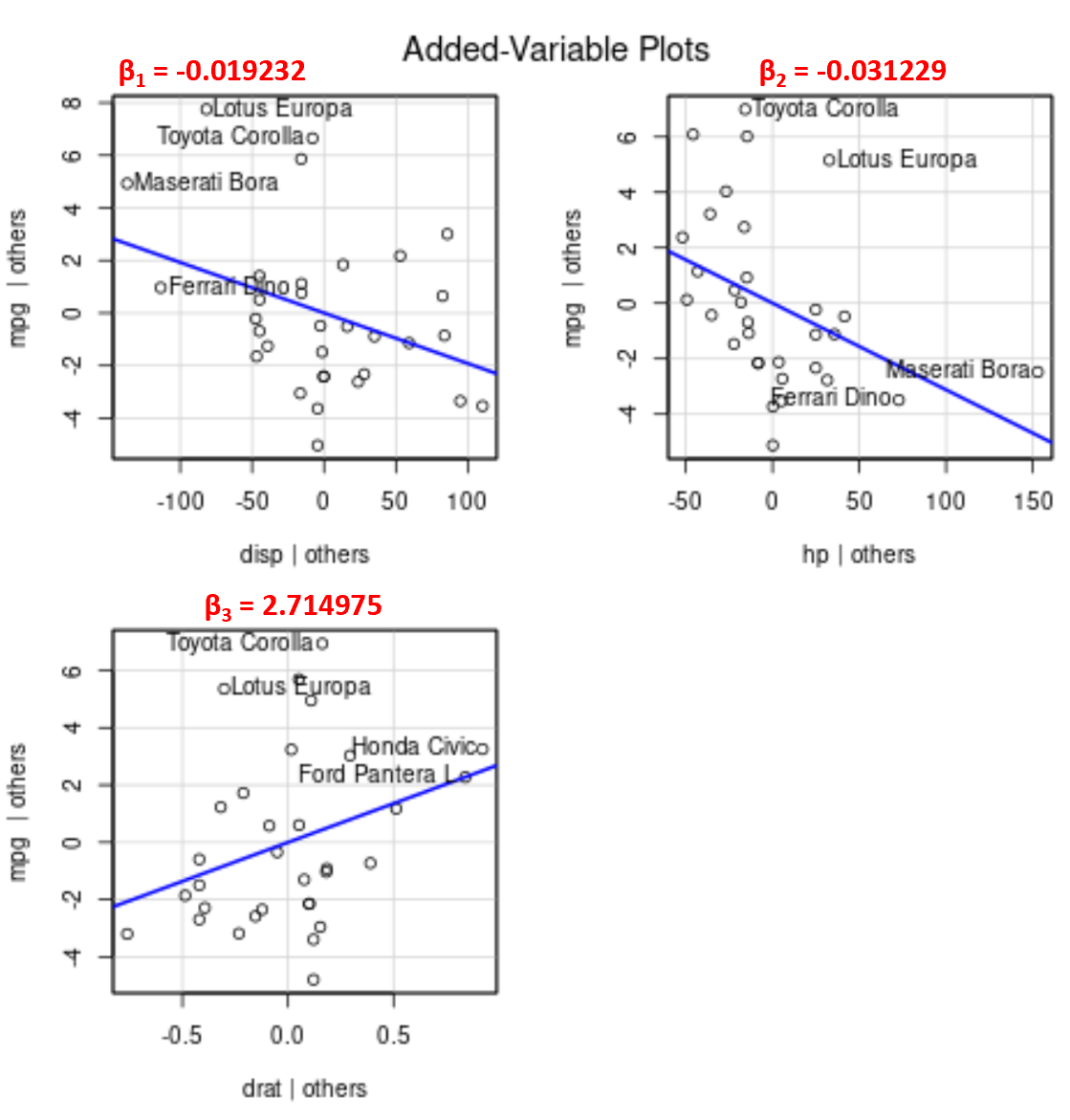
Birden fazla öngörücü değişkenimiz olduğu için 2 boyutlu bir grafik üzerinde tek bir uygun regresyon çizgisi çizemesek de, bu eklenen değişken grafikler, diğer öngörücü değişkenleri sabit tutarken her bir yordayıcı değişken ile yanıt değişkeni arasındaki ilişkiyi gözlemlememize olanak tanır.