Optimum kümeleri bulmak için r'de dirsek yöntemi nasıl kullanılır?

Makine öğreniminde en sık kullanılan kümeleme algoritmalarından biri k-ortalama kümeleme olarak bilinir.

K-ortalama kümelemesi, bir veri kümesindeki her gözlemi K kümesinden birine yerleştirdiğimiz bir tekniktir.

Nihai amaç, her küme içindeki gözlemlerin birbirine oldukça benzer olduğu, farklı kümelerdeki gözlemlerin ise birbirinden oldukça farklı olduğu K kümeye sahip olmaktır.

K-ortalamalı kümeleme yaparken ilk adım, gözlemleri yerleştirmek istediğimiz kümelerin sayısı olan K için bir değer seçmektir.

K için bir değer seçmenin en yaygın yollarından biri, x ekseninde küme sayısı ve y ekseninde karelerin toplamından oluşan bir grafik oluşturmayı ve ardından K değerini belirlemeyi içeren dirsek yöntemi olarak bilinir. olay örgüsünde bir “diz” veya dönüşün göründüğü yer.

X ekseninde “dizin” oluştuğu nokta bize k-ortalamalı kümeleme algoritmasında kullanılacak en uygun küme sayısını söyler.

Aşağıdaki örnek R’de dirsek yönteminin nasıl kullanılacağını gösterir.

Örnek: R’de Dirsek Yöntemini Kullanmak

Bu örnek için, 1973’te her ABD eyaletinde 100.000 kişi başına cinayet, saldırı ve tecavüz nedeniyle tutuklananların sayısını ve ayrıca her eyaletin kentsel bölgelerde yaşayan nüfusunun yüzdesini içeren, R’de yerleşik USArrests veri kümesini kullanacağız. alanlar. , UrbanPop.

Aşağıdaki kod, veri kümesinin nasıl yükleneceğini, eksik değerleri olan satırların nasıl kaldırılacağını ve veri kümesindeki her değişkenin ortalaması 0 ve standart sapması 1 olacak şekilde nasıl ölçekleneceğini gösterir:

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

K-means algoritmasında kullanılacak en uygun küme sayısını bulmak için, factoextra paketindeki fviz_nbclust() işlevini kullanarak küme sayısı ile kareler toplamı toplamının grafiğini oluşturacağız:

 library (cluster)
library (factoextra)

#create plot of number of clusters vs total within sum of squares
fviz_nbclust(df, kmeans, method = “ wss ”) 

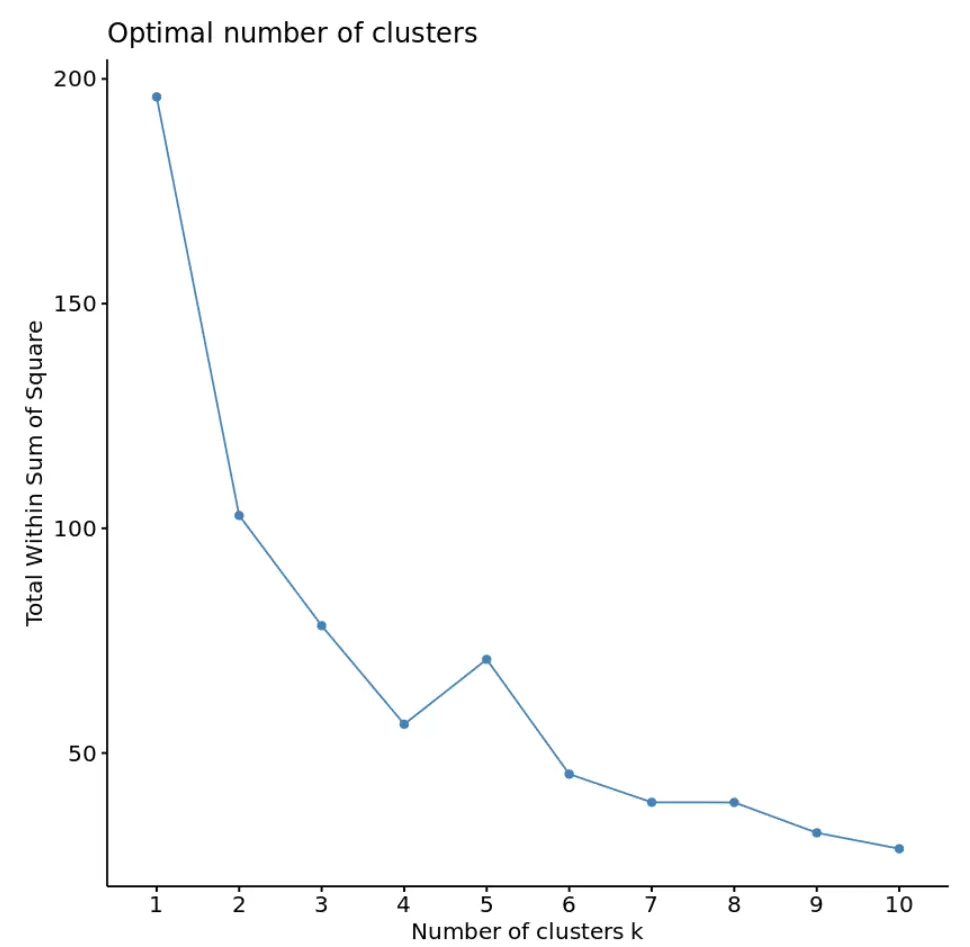
Bu grafikte k = 4 kümede bir “diz” veya bükülme olduğu görülmektedir. Bu, kareler toplamındaki toplamın istikrar kazanmaya başladığı noktadır.

Bu bize k-ortalamalar algoritmasında kullanılacak en uygun küme sayısının 4 olduğunu söyler.

Not : Daha fazla küme kullanarak kareler toplamında daha düşük bir toplam elde edebilsek de, muhtemelen eğitim verilerini gereğinden fazla sığdırırız ve bu nedenle k-ortalamalar algoritması test verileri üzerinde iyi çalışmaz.

K 4 için en uygun değeri kullanarak veri kümesinde k-means kümelemesini gerçekleştirmek için küme paketindeki kmeans() işlevini kullanabiliriz:

 #make this example reproducible
set. seeds (1)

#perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)

#view results
km

K-means clustering with 4 clusters of sizes 16, 13, 13, 8

Cluster means:
      Murder Assault UrbanPop Rape
1 -0.4894375 -0.3826001 0.5758298 -0.26165379
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 0.6950701 1.0394414 0.7226370 1.27693964
4 1.4118898 0.8743346 -0.8145211 0.01927104

Vector clustering:
       Alabama Alaska Arizona Arkansas California Colorado 
             4 3 3 4 3 3 
   Connecticut Delaware Florida Georgia Hawaii Idaho 
             1 1 3 4 1 2 
      Illinois Indiana Iowa Kansas Kentucky Louisiana 
             3 1 2 1 2 4 
         Maine Maryland Massachusetts Michigan Minnesota Mississippi 
             2 3 1 3 2 4 
      Missouri Montana Nebraska Nevada New Hampshire New Jersey 
             3 2 2 3 2 1 
    New Mexico New York North Carolina North Dakota Ohio Oklahoma 
             3 3 4 2 1 1 
        Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 
             1 1 1 4 2 4 
         Texas Utah Vermont Virginia Washington West Virginia 
             3 1 2 1 1 2 
     Wisconsin Wyoming 
             2 1 

Within cluster sum of squares by cluster:
[1] 16.212213 11.952463 19.922437 8.316061
 (between_SS / total_SS = 71.2%)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"   
[7] "size" "iter" "ifault"         

Sonuçlardan şunu görebiliriz:

• İlk kümeye 16 eyalet atandı
• İkinci kümeye 13 eyalet atandı
• Üçüncü kümeye 13 eyalet atandı
• Dördüncü kümeye 8 eyalet atandı

Ayrıca her bir durumun küme atamalarını orijinal veri kümesine ekleyebiliriz:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

	Murder Assault UrbanPop Rape cluster
				
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

Orijinal veri tabanındaki her gözlem dört gruptan birine yerleştirildi.

Ek kaynaklar

Aşağıdaki eğitimlerde, R’de çeşitli kümeleme algoritmalarının nasıl çalıştırılacağına ilişkin adım adım örnekler verilmektedir:

R’de K-Ortalama Kümeleme: Adım Adım Örnek
R’de K-Medoids Kümelemesi: Adım Adım Örnek
R’de Hiyerarşik Kümeleme: Adım Adım Örnek