R'de en küçük kareler yöntemi nasıl kullanılır?

En küçük kareler yöntemi, belirli bir veri kümesine en iyi uyan regresyon doğrusunu bulmak için kullanabileceğimiz bir yöntemdir.

R’ye bir regresyon çizgisi sığdırmak amacıyla en küçük kareler yöntemini kullanmak için lm() işlevini kullanabiliriz.

Bu işlev aşağıdaki temel sözdizimini kullanır:

 model <- lm(response ~ predictor, data=df)

Aşağıdaki örnek bu işlevin R’de nasıl kullanılacağını gösterir.

Örnek: R’de en küçük kareler yöntemi

R’de, bir sınıftaki 15 öğrencinin çalışılan saat sayısını ve karşılık gelen sınav puanını gösteren aşağıdaki veri çerçevesine sahip olduğumuzu varsayalım:

 #create data frame
df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of data frame
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

Bu verilere bir regresyon çizgisi sığdırmak amacıyla en küçük kareler yöntemini kullanmak için lm() işlevini kullanabiliriz:

 #use method of least squares to fit regression line
model <- lm(score ~ hours, data=df)

#view regression model summary
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

Tahmini Sonuç sütunundaki değerlerden aşağıdaki uygun regresyon satırını yazabiliriz:

Sınav puanı = 65.334 + 1.982 (saat)

Modeldeki her bir katsayının nasıl yorumlanacağı aşağıda açıklanmıştır:

• Intercept : 0 saat ders çalışan bir öğrenci için beklenen sınav puanı 65.334’tür .
• saat : Çalışılan her ek saat için beklenen sınav puanı 1.982 artar.

Bir öğrencinin çalışma saatlerine göre alacağı sınav notunu tahmin etmek için bu denklemi kullanabiliriz.

Örneğin bir öğrenci 5 saat çalışıyorsa sınav puanının 75.244 olacağını tahmin ediyoruz:

Sınav Puanı = 65,334 + 1,982(5) = 75,244

Son olarak, arsa üzerine bindirilmiş uygun regresyon çizgisiyle orijinal verilerin bir dağılım grafiğini oluşturabiliriz:

 #create scatter plot of data
plot(df$hours, df$score, pch=16, col=' steelblue ')

#add fitted regression line to scatter plot
abline(model)

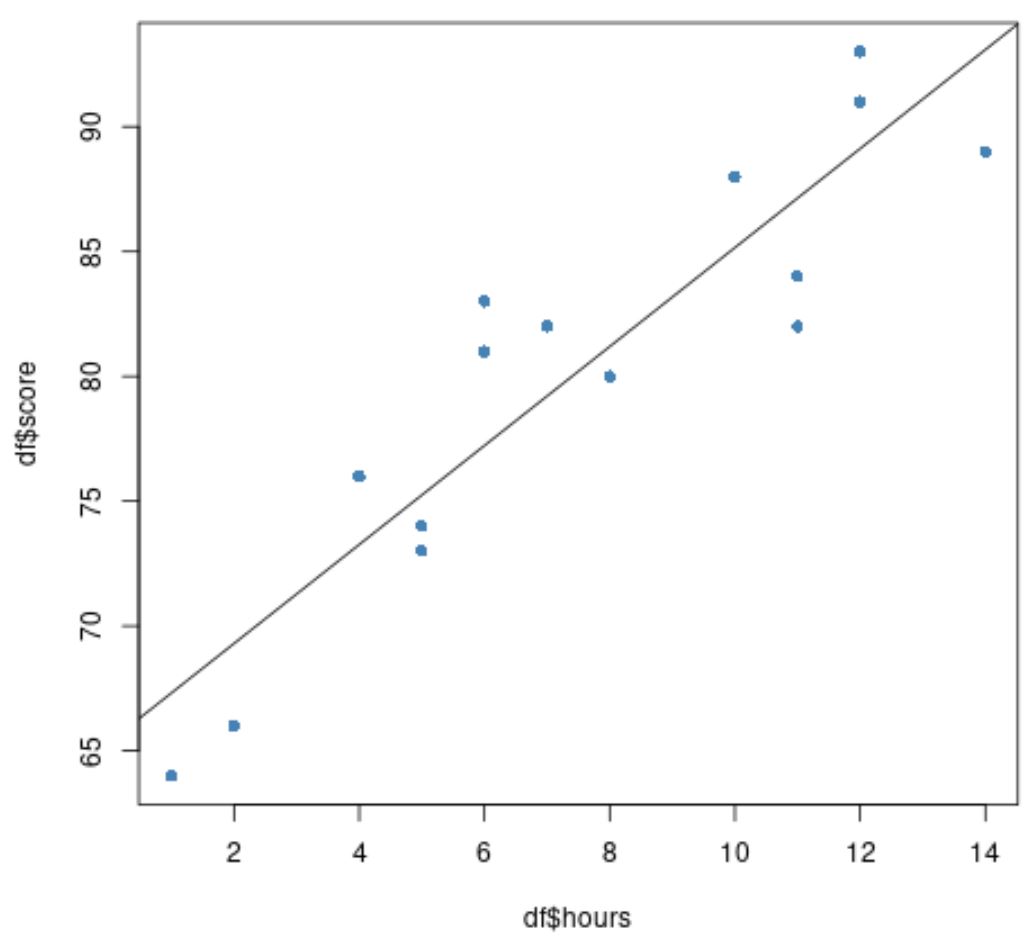
Mavi daireler verileri, siyah çizgi ise takılan regresyon çizgisini temsil eder.

Ek kaynaklar

Aşağıdaki eğitimlerde R’de diğer ortak görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

R’de artık arsa nasıl oluşturulur
R’de çoklu doğrusallık nasıl test edilir
R’de eğri uydurma nasıl gerçekleştirilir