R'de log rank testi nasıl yapılır?

Log-rank testi, iki grup arasındaki hayatta kalma eğrilerini karşılaştırmanın en yaygın yoludur.

Bu test aşağıdaki varsayımları kullanır:

H ₀ : İki grup arasında hayatta kalma açısından fark yok.

H _A : İki grup arasında hayatta kalma açısından fark var .

Testin p değeri belirli bir anlamlılık düzeyinin altındaysa (örneğin α = 0,05), o zaman sıfır hipotezini reddedebilir ve iki grup arasında hayatta kalma açısından bir fark olduğunu söylemek için yeterli kanıt olduğu sonucuna varabiliriz.

R’de bir log-rank testi gerçekleştirmek için aşağıdaki sözdizimini kullanan hayatta kalma paketindeki survdiff() işlevini kullanabiliriz:

survdiff(Surv(zaman, durum) ~ tahminciler, veriler)

Bu fonksiyon bir ki-kare testi istatistiği ve buna karşılık gelen bir p değeri döndürür.

Aşağıdaki örnek, R’de bir log-sıra testi gerçekleştirmek için bu işlevin nasıl kullanılacağını gösterir.

Örnek: R’de Günlük Sıralaması Testi

Bu örnek için hayatta kalma paketindeki yumurtalık veri setini kullanacağız. Bu veri seti 26 hastaya ilişkin aşağıdaki bilgileri içermektedir:

• Yumurtalık kanseri teşhisi konulduktan sonra hayatta kalma süresi (ay cinsinden)
• Hayatta kalma süresinin sansürlenip sansürlenmediği
• Alınan tedavinin türü (rx = 1 veya rx = 2)

Aşağıdaki kod, bu veri kümesinin ilk altı satırının nasıl görüntüleneceğini gösterir:

 library (survival)

#view first six rows of dataset
head(ovarian)

  futime fustat age resid.ds rx ecog.ps
1 59 1 72.3315 2 1 1
2 115 1 74.4932 2 1 1
3 156 1 66.4658 2 1 2
4 421 0 53.3644 2 2 1
5,431 1 50.3397 2 1 1
6 448 0 56.4301 1 1 2

Aşağıdaki kod, farklı tedaviler alan hastalar arasında hayatta kalma açısından bir fark olup olmadığını belirlemek için log-sıra testinin nasıl gerçekleştirileceğini gösterir:

 #perform log rank test
survdiff(Surv(futime, fustat) ~ rx, data=ovarian)

Call:
survdiff(formula = Surv(futime, fustat) ~ rx, data = ovarian)

      N Observed Expected (OE)^2/E (OE)^2/V
rx=1 13 7 5.23 0.596 1.06
rx=2 13 5 6.77 0.461 1.06

 Chisq= 1.1 on 1 degrees of freedom, p= 0.3 

Ki-kare test istatistiği 1 serbestlik derecesi ile 1,1’dir ve karşılık gelen p değeri 0,3’tür . Bu p değeri 0,05’ten küçük olmadığından sıfır hipotezini reddedemiyoruz.

Başka bir deyişle, iki tedavi arasında hayatta kalma açısından istatistiksel olarak anlamlı bir fark olduğunu söyleyecek yeterli kanıtımız yok.

Aşağıdaki sözdizimini kullanarak her grup için hayatta kalma eğrilerini de çizebiliriz:

 #plot survival curves for each treatment group
plot(survfit(Surv(futime, fustat) ~ rx, data = ovarian), 
     xlab = " Time ", 
     ylab = “ Overall survival probability ”)

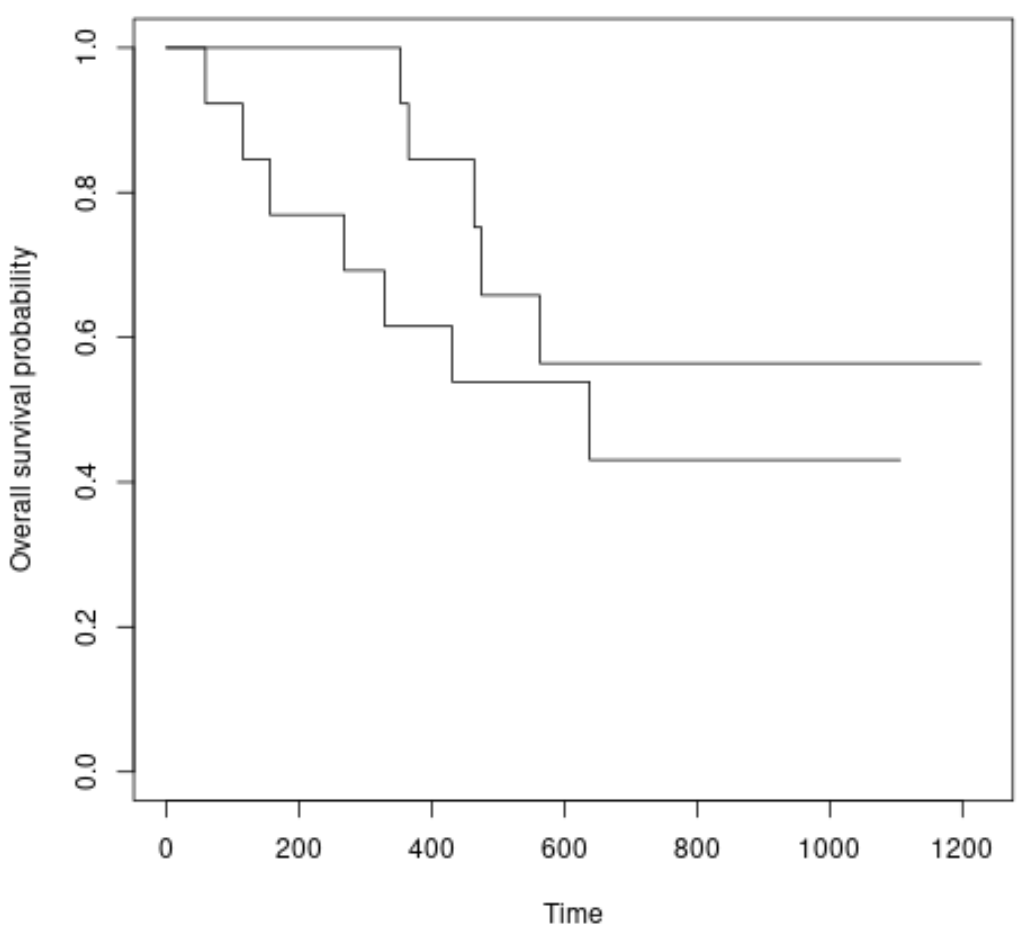
Hayatta kalma eğrilerinin biraz farklı olduğunu görebiliyoruz ancak log-rank testi bize farkın istatistiksel olarak anlamlı olmadığını gösterdi.