R'de i̇ki değişkenli analiz nasıl gerçekleştirilir (örneklerle)

İki değişkenli analiz terimi, iki değişkenin analizini ifade eder. Bunu “bi” ön ekinin “iki” anlamına gelmesinden dolayı hatırlayabilirsiniz.

İki değişkenli analizin amacı iki değişken arasındaki ilişkiyi anlamaktır.

İki değişkenli analiz gerçekleştirmenin üç yaygın yolu vardır:

1. Nokta bulutları

2. Korelasyon katsayıları

3. Basit doğrusal regresyon

Aşağıdaki örnek, iki değişken hakkında bilgi içeren aşağıdaki veri kümesini kullanarak bu iki değişkenli analiz türlerinin her birinin nasıl gerçekleştirileceğini gösterir: (1) Çalışmak için harcanan saatler ve (2) 20 farklı öğrenci tarafından kazanılan test puanları:

 #create data frame
df <- data. frame (hours=c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                         3, 4, 4, 5, 5, 6, 6, 6, 7, 8),
                 score=c(75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                         80, 88, 85, 90, 92, 94, 94, 88, 91, 96))

#view first six rows of data frame
head(df)

  hours score
1 1 75
2 1 66
3 1 68
4 2 74
5 2 78
6 2 72

1. Nokta bulutları

R’de çalışılan saatlerin sınav notlarına göre dağılım grafiğini oluşturmak için aşağıdaki sözdizimini kullanabiliriz:

 #create scatterplot of hours studied vs. exam score
plot(df$hours, df$score, pch= 16 , col=' steelblue ',
     main=' Hours Studied vs. Exam Score ',
     xlab=' Hours Studied ', ylab=' Exam Score ')

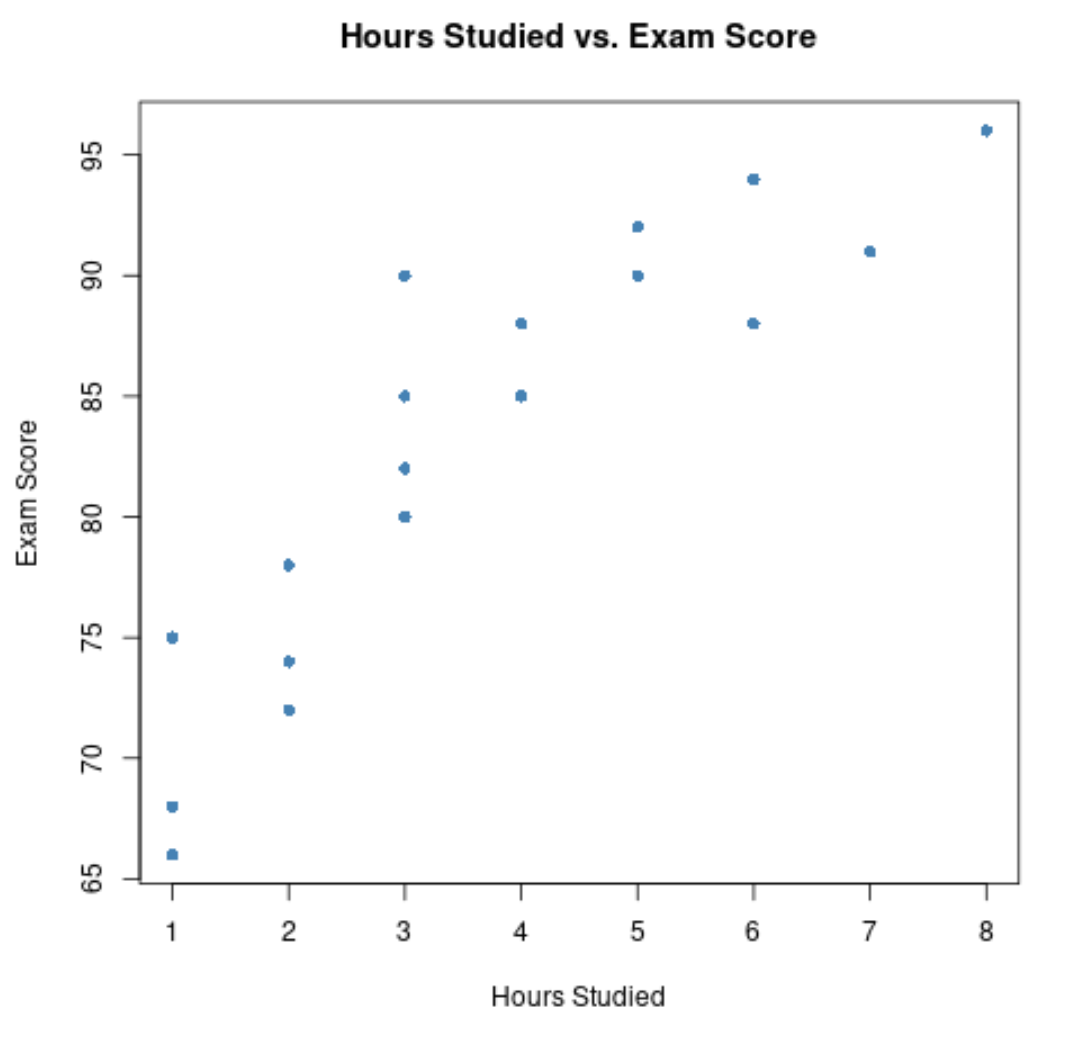
X ekseni çalışılan saatleri, y ekseni ise sınavda alınan notu gösterir.

Grafik, iki değişken arasında pozitif bir ilişki olduğunu göstermektedir: Çalışma saati arttıkça sınav puanları da artma eğilimindedir.

2. Korelasyon katsayıları

Pearson korelasyon katsayısı, iki değişken arasındaki doğrusal ilişkiyi ölçmenin bir yoludur.

İki değişken arasındaki Pearson korelasyon katsayısını hesaplamak için R’deki cor() fonksiyonunu kullanabiliriz:

 #calculate correlation between hours studied and exam score received
cor(df$hours, df$score)

[1] 0.891306

Korelasyon katsayısı 0,891 olarak çıkıyor.

Bu değerin 1’e yakın olması çalışılan saat ile sınav notu arasında güçlü bir pozitif korelasyon olduğunu göstermektedir.

3. Basit doğrusal regresyon

Basit doğrusal regresyon, bir veri kümesine en iyi “uyan” doğrunun denklemini bulmak için kullanabileceğimiz istatistiksel bir yöntemdir ve bunu daha sonra iki değişken arasındaki kesin ilişkiyi anlamak için kullanabiliriz.

Çalışılan saatler ve alınan sınav sonuçları için basit bir doğrusal regresyon modeline uyacak şekilde R’deki lm() işlevini kullanabiliriz:

 #fit simple linear regression model
fit <- lm(score ~ hours, data=df)

#view summary of model
summary(fit)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-6,920 -3,927 1,309 1,903 9,385 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 69.0734 1.9651 35.15 < 2nd-16 ***
hours 3.8471 0.4613 8.34 1.35e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.171 on 18 degrees of freedom
Multiple R-squared: 0.7944, Adjusted R-squared: 0.783 
F-statistic: 69.56 on 1 and 18 DF, p-value: 1.347e-07

Uygun regresyon denklemi şu şekilde ortaya çıkıyor:

Sınav puanı = 69.0734 + 3.8471*(çalışma saati)

Bu bize, çalışılan her ek saatin sınav puanında ortalama 3,8471 artışla ilişkili olduğunu söylüyor.

Bir öğrencinin toplam ders saatine göre alacağı puanı tahmin etmek için uygun regresyon denklemini de kullanabiliriz.

Örneğin 3 saat ders çalışan bir öğrencinin 81.6147 puan alması gerekir:

• Sınav puanı = 69.0734 + 3.8471*(çalışma saati)
• Sınav puanı = 69,0734 + 3,8471*(3)
• Sınav sonucu = 81.6147

Ek kaynaklar

Aşağıdaki eğitimler iki değişkenli analiz hakkında ek bilgi sağlar:

İki Değişkenli Analize Giriş
Gerçek hayatta iki değişkenli verilere 5 örnek
Basit Doğrusal Regresyona Giriş