R'de i̇ki değişkenli normal dağılım nasıl simüle edilir ve çizilir

İstatistikte iki değişken, toplandığında normal dağılıma sahipse iki değişkenli normal dağılım izler.

Bu eğitimde R’de aşağıdaki görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

• İki değişkenli normal dağılımı simüle edin
• Kontur grafiği (2B çizim) kullanarak iki değişkenli normal dağılımın grafiğini çizin
• Bir yüzey grafiği (3B çizim) kullanarak iki değişkenli normal dağılımın grafiğini çizin

Hadi gidelim!

Örnek 1: R’de iki değişkenli normal dağılımı simüle edin

R’de iki değişkenli normal dağılımı simüle etmenin en basit yolu, MASS paketindeki mvrnorm() işlevini kullanmaktır.

Aşağıdaki kod, pratikte iki değişkenli normal dağılımı simüle etmek için bu işlevin nasıl kullanılacağını gösterir:

 library (MASS)

#make this example reproducible
set. seed ( 0 )

#simulate bivariate normal distribution
bivariate_data <- as. data . frame (mvrnorm(n= 100 ,
                                        mu=c(0, 0),
                                        Sigma=matrix(c(5, 3, 4, 4), ncol= 2 )))

#view first six rows of bivariate dataset
head(bivariate_data)

           V1 V2
1 -2.03600343 -2.9623059
2 0.07719131 1.2948982
3 -3.26729701 -1.7928069
4 -2.62985132 -2.3015471
5 -1.75126215 0.3056698
6 3.67698436 2.2020238

mvrnorm() işlevine ilişkin her bağımsız değişkenin yaptığı şey aşağıdadır:

• n : Örnek boyutunu tanımlar
• mu : Her değişkenin ortalamasını tanımlar
• Sigma : İki değişkenin kovaryans matrisini tanımlar

Nihai sonuç, birbirine eklendiğinde normal bir dağılım izleyen iki değişkenli bir veri çerçevesidir.

Örnek 2: İki Değişkenli Normal Dağılımın Çizilmesi

R’de iki değişkenli normal dağılımı çizmenin en kolay yolu mnormt() paketindeki işlevleri kullanmaktır.

Örneğin, iki değişkenli normal dağılımın 2 boyutlu görselleştirmesini sağlayan bir kontur grafiği oluşturmak için bu paketin kontur() fonksiyonunu kullanabiliriz:

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create contour plot
contour(x, y, z)

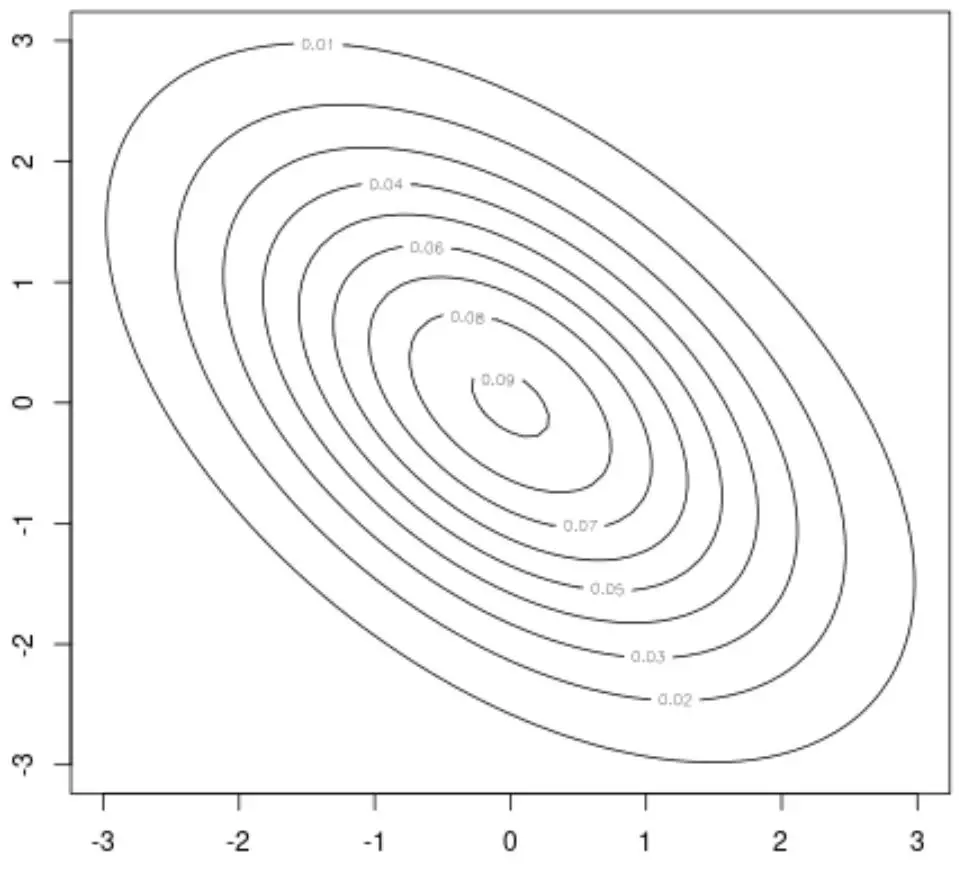
İki değişkenli normal dağılımın 3 boyutlu görselleştirmesini sağlayan bir yüzey grafiği oluşturmak için persp() işlevini de kullanabiliriz:

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create surface plot
persp(x, y, z, theta= -30 , phi= 25 , expand= 0.6 , ticktype=' detailed ')

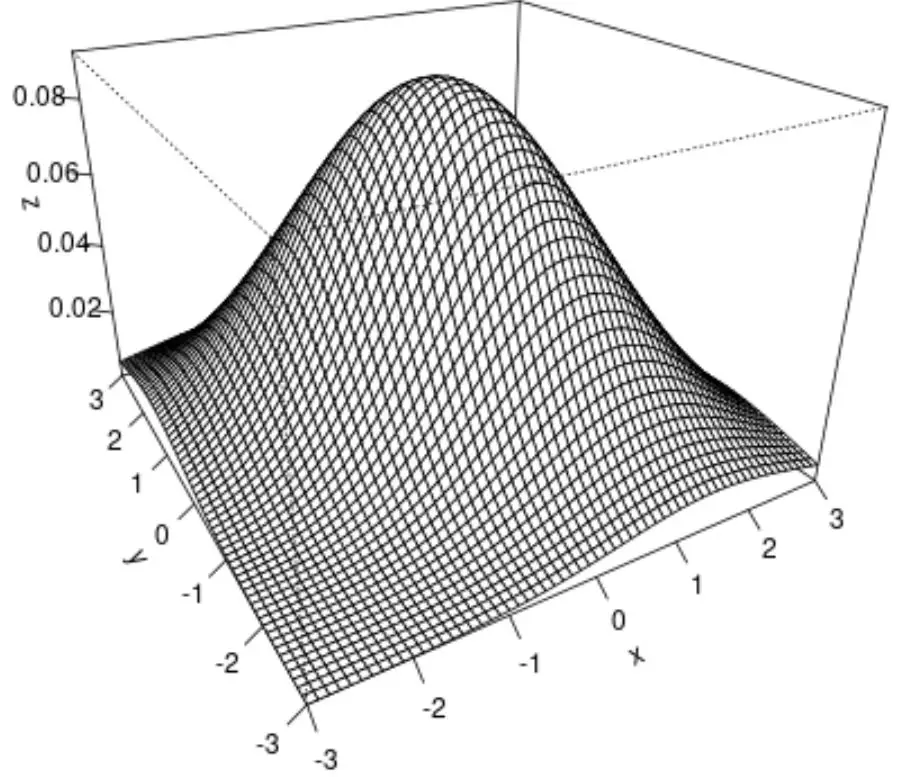
persp() işlevine ilişkin her argümanın yaptığı şey:

• theta, phi : İzleme yönü açılarını ayarlar.
• genişlet : Z ekseninin boyutunu kontrol eder.
• Ticktype : Eksenler üzerindeki onay işaretlerinin görünümünü kontrol eder.

Nihai sonuç, iki değişkenli normal dağılımın 3 boyutlu yüzey grafiğidir.

Ek kaynaklar

Aşağıdaki eğitimler R’de diğer olasılık dağılımlarının nasıl kullanılacağını açıklamaktadır:

R’de normal dağılım nasıl kullanılır?
R’de binom dağılımı nasıl kullanılır?
R’de Poisson dağılımı nasıl kullanılır?
R’de çok terimli dağılım nasıl kullanılır?