R'de brown – forsythe testi: adım adım örnek

Üç veya daha fazla bağımsız grubun ortalamaları arasında anlamlı bir fark olup olmadığını belirlemek için tek yönlü ANOVA kullanılır.

Tek yönlü ANOVA’nın varsayımlarından biri, örneklerin alındığı popülasyonların varyanslarının eşit olmasıdır.

Bunu test etmenin en yaygın yollarından biri, aşağıdaki varsayımları kullanan istatistiksel bir test olan Brown-Forsythe testini kullanmaktır:

• H ₀ : Popülasyonlar arasındaki varyanslar eşittir.
• H _A : Popülasyonlar arasındaki farklar eşit değildir.

Testin p değeri belirli bir anlamlılık düzeyinin altındaysa (örneğin α = 0,05), o zaman boş hipotezi reddederiz ve varyansların farklı popülasyonlar arasında eşit olmadığı sonucuna varırız.

Bu eğitimde R’de Brown-Forsythe testinin nasıl gerçekleştirileceğine ilişkin adım adım bir örnek sunulmaktadır.

1. Adım: Verileri girin

Üç farklı egzersiz programının farklı düzeylerde kilo kaybına yol açıp açmadığını bilmek istediğimizi varsayalım.

Bunu test etmek için 90 kişiyi işe alıyoruz ve her programı kullanması için rastgele 30 kişiyi görevlendiriyoruz. Daha sonra her kişinin bir ay sonraki kilo kaybını ölçüyoruz.

Aşağıdaki veri seti, her programda kaybedilen kilo miktarına ilişkin bilgiler içerir:

 #make this example reproducible
set.seed(0)

#create data frame
data <- data.frame(program = as . factor ( rep (c(" A ", " B ", " C "), each = 30)),
                   weight_loss = c( runif (30, 0, 3),
                                   runif (30, 0, 5),
                                   runif (30, 1, 7)))

#view first six rows of data frame
head(data)

# program weight_loss
#1 A 2.6900916
#2 A 0.7965260
#3 A 1.1163717
#4 A 1.7185601
#5 A 2.7246234
#6 A 0.6050458

Adım 2: Verileri özetleyin ve görselleştirin

Brown-Forsythe testini gerçekleştirmeden önce, her grup için kilo kaybındaki varyansı görselleştirmek için kutu grafikleri oluşturabiliriz:

 boxplot(weight_loss ~ program, data = data)

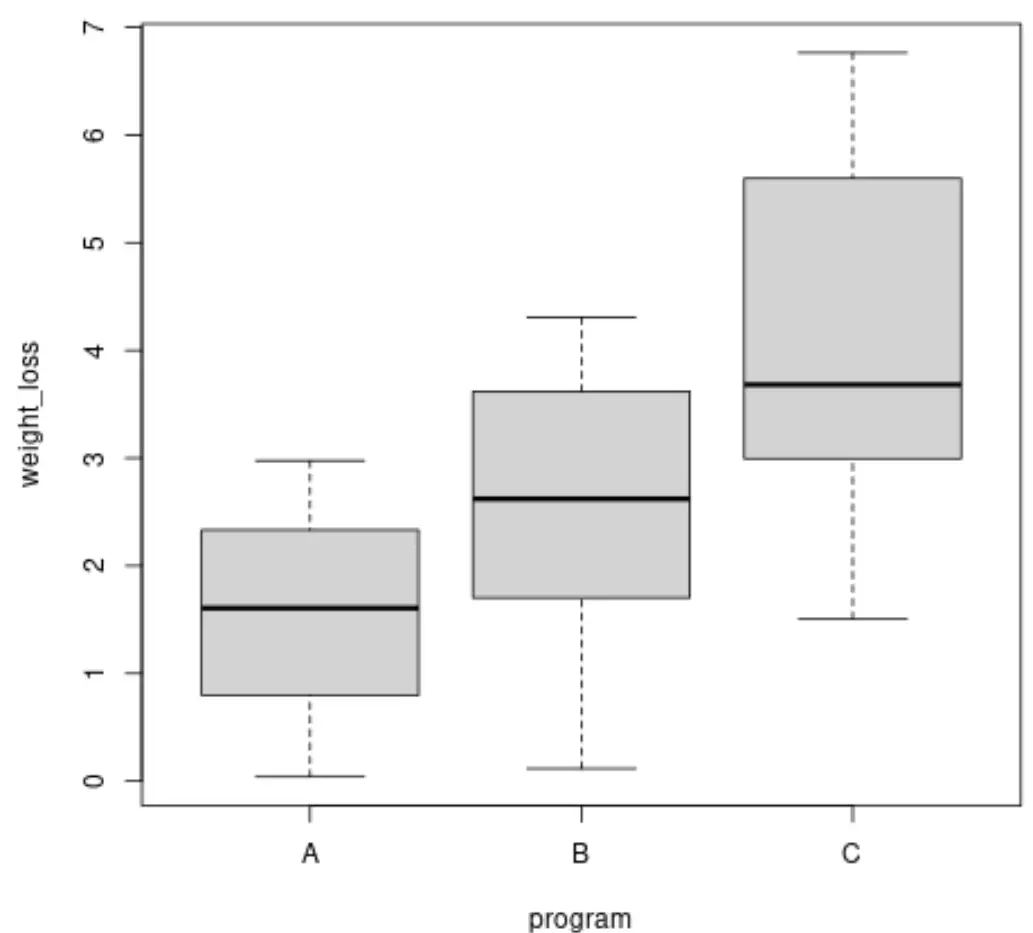
Ayrıca her gruptaki kilo kaybının varyansını da hesaplayabiliriz:

 #load dplyr package
library (dplyr)

#calculate variance of weight loss by group
data %>%
group_by (program) %>%
  summarize (var=var(weight_loss))

# A tibble: 3 x 2
  program var
     
1 A 0.819
2 B 1.53 
3 C 2.46

Gruplar arası varyansların farklı olduğunu görebiliriz ancak bu farklılıklarınistatistiksel olarak anlamlı olup olmadığını belirlemek için Brown-Forsythe testini yapabiliriz.

Adım 3: Brown-Forsythe testini gerçekleştirin

R’de Brown-Forsythe testi gerçekleştirmek için onewaytests paketindeki bf.test() işlevini kullanabiliriz:

 #load onewaytests package
library (onewaytests)

#perform Brown-Forsythe test
bf.test(weight_loss ~ program, data = data)

  Brown-Forsythe Test (alpha = 0.05) 
-------------------------------------------------- ----------- 
  data: weight_loss and program 

  statistic: 30.83304 
  num df: 2 
  name df: 74.0272 
  p.value: 1.816529e-10 

  Result: Difference is statistically significant. 
-------------------------------------------------- -----------

Testin p değeri 0,000’den küçük çıkıyor ve sonucun da gösterdiği gibi, üç grup arasındaki varyans farklılıkları istatistiksel olarak anlamlı.

Sonraki adımlar

Brown-Forsythe testinin sıfır hipotezini reddedemiyorsanız veriler üzerinde tek yönlü ANOVA gerçekleştirebilirsiniz.

Ancak sıfır hipotezinin reddedilmesi varyansların eşitliği varsayımının ihlal edildiği anlamına gelir. Bu durumda iki seçeneğiniz var:

1. Yine de tek yönlü bir ANOVA yapın.

En büyük varyans en küçük varyansın 4 katından büyük olmadığı sürece tek yönlü bir ANOVA’nın aslında eşit olmayan varyanslara karşı dayanıklı olduğu ortaya çıktı.

Yukarıdaki örneğin 2. adımında en küçük varyansın 0,819, en büyük varyansın ise 2,46 olduğunu bulduk. Yani en büyük varyansın en küçüğüne oranı 2,46 / 0,819 = 3,003’tür .

Bu değer 4’ten küçük olduğundan tek yönlü ANOVA’yı yapabiliriz.

2. Kruskal-Wallis testi yapın

En büyük varyansın en küçük varyansa oranı 4’ten büyükse bunun yerine Kruskal-Wallis testi yapılabilir. Bu, tek yönlü ANOVA’nın parametrik olmayan eşdeğeri olarak kabul edilir.

R’de Kruskal-Wallis testinin adım adım örneğini burada bulabilirsiniz.