R'de kaldıraç istatistikleri nasıl hesaplanır

İstatistikte, bir gözlemin yanıt değişkenine ilişkin değeri veri kümesindeki diğer gözlemlerden çok daha büyükse, bu gözlem aykırı değer olarak kabul edilir.

Benzer şekilde, bir gözlem, veri kümesindeki diğer gözlemlerle karşılaştırıldığında çok daha ekstrem tahmin değişkenleri için bir veya daha fazla değere sahipse, yüksek kaldıraç olarak kabul edilir.

Herhangi bir analiz türünde ilk adımlardan biri, belirli bir modelin sonuçları üzerinde büyük bir etkiye sahip olabileceğinden, yüksek etkiye sahip gözlemlere daha yakından bakmaktır.

Bu eğitimde, R’deki bir modeldeki her gözlem için kaldıracın nasıl hesaplanacağı ve görselleştirileceğine ilişkin adım adım bir örnek gösterilmektedir.

1. Adım: Bir regresyon modeli oluşturun

İlk olarak, R’de yerleşik mtcars veri kümesini kullanarak çoklu doğrusal regresyon modeli oluşturacağız:

 #load the dataset
data(mtcars)

#fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Adım 2: Her gözlem için kaldıracı hesaplayın

Daha sonra, modeldeki her gözlemin kaldıracını hesaplamak için hatvalues() fonksiyonunu kullanacağız:

 #calculate leverage for each observation in the model
hats <- as . data . frame (hatvalues(model))

#display leverage stats for each observation
hats

                    hatvalues(model)
Mazda RX4 0.04235795
Mazda RX4 Wag 0.04235795
Datsun 710 0.06287776
Hornet 4 Drive 0.07614472
Hornet Sportabout 0.08097817
Valiant 0.05945972
Duster 360 0.09828955
Merc 240D 0.08816960
Merc 230 0.05102253
Merc 280 0.03990060
Merc 280C 0.03990060
Merc 450SE 0.03890159
Merc 450SL 0.03890159
Merc 450SLC 0.03890159
Cadillac Fleetwood 0.19443875
Lincoln Continental 0.16042361
Chrysler Imperial 0.12447530
Fiat 128 0.08346304
Honda Civic 0.09493784
Toyota Corolla 0.08732818
Toyota Corona 0.05697867
Dodge Challenger 0.06954069
AMC Javelin 0.05767659
Camaro Z28 0.10011654
Pontiac Firebird 0.12979822
Fiat X1-9 0.08334018
Porsche 914-2 0.05785170
Lotus Europa 0.08193899
Ford Pantera L 0.13831817
Ferrari Dino 0.12608583
Maserati Bora 0.49663919
Volvo 142E 0.05848459

Genellikle kaldıraç değeri 2’den büyük olan gözlemlere daha yakından bakarız.

Bunu yapmanın basit bir yolu, gözlemleri kaldıraç değerlerine göre azalan düzende sıralamaktır:

 #sort observations by leverage, descending
hats[ order (-hats[' hatvalues(model) ']), ]

 [1] 0.49663919 0.19443875 0.16042361 0.13831817 0.12979822 0.12608583
 [7] 0.12447530 0.10011654 0.09828955 0.09493784 0.08816960 0.08732818
[13] 0.08346304 0.08334018 0.08193899 0.08097817 0.07614472 0.06954069
[19] 0.06287776 0.05945972 0.05848459 0.05785170 0.05767659 0.05697867
[25] 0.05102253 0.04235795 0.04235795 0.03990060 0.03990060 0.03890159
[31] 0.03890159 0.03890159

En yüksek kaldıraç değerinin 0,4966 olduğunu görebiliyoruz. Bu sayı 2’den büyük olmadığından veri setimizdeki gözlemlerin hiçbirinin yüksek kaldıraca sahip olmadığını biliyoruz.

3. Adım: Her gözlemin etkisini görselleştirin

Son olarak, her gözlemin etkisini görselleştirmek için hızlı bir grafik oluşturabiliriz:

 #plot leverage values for each observation
plot(hatvalues(model), type = ' h ')

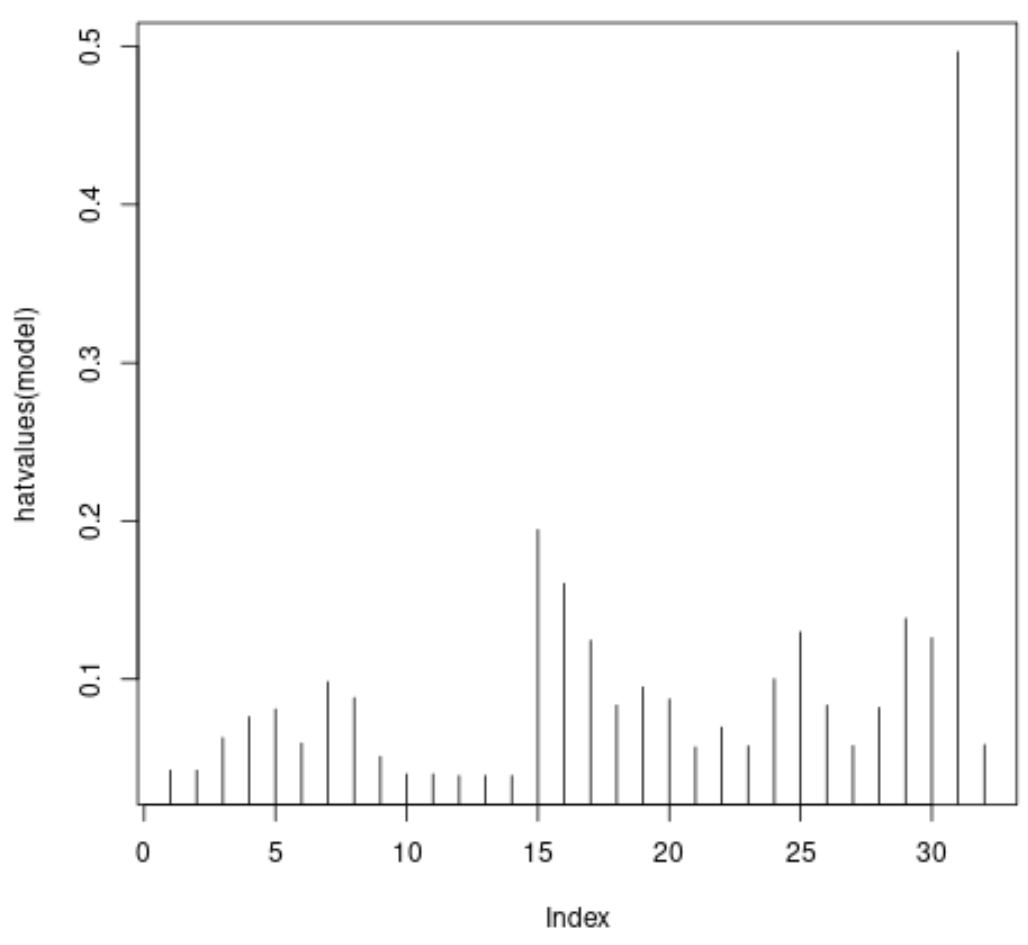
X ekseni veri kümesindeki her gözlemin indeksini görüntüler ve y değeri ise her gözlem için karşılık gelen kaldıraç istatistiğini görüntüler.

Ek kaynaklar

R’de basit doğrusal regresyon nasıl gerçekleştirilir
R’de çoklu doğrusal regresyon nasıl gerçekleştirilir
R’de artık arsa nasıl oluşturulur