R'de kısmi artık grafikler nasıl oluşturulur

Çoklu doğrusal regresyon, birden fazla yordayıcı değişken ile bir yanıt değişkeni arasındaki ilişkiyi anlamak için kullanabileceğimiz istatistiksel bir yöntemdir.

Ancak çoklu doğrusal regresyonun temel varsayımlarından biri, her yordayıcı değişken ile yanıt değişkeni arasında doğrusal bir ilişkinin olmasıdır.

Bu varsayım karşılanmazsa regresyon modelinin sonuçları güvenilir olmayabilir.

Bu varsayımı test etmenin bir yolu, bir yordayıcı değişkenin yanıt değişkenine göre artıklarını görüntüleyen bir kısmi artıklar grafiği oluşturmaktır.

Aşağıdaki örnek, R’de bir regresyon modeli için kısmi artık grafiklerinin nasıl oluşturulacağını gösterir.

Örnek: R’de kısmi artık grafikleri nasıl oluşturulur?

R’de üç öngörücü değişkene sahip bir regresyon modeline uyduğumuzu varsayalım:

 #make this example reproducible
set. seeds (0)

#define response variable
y <- c(1:1000)

#define three predictor variables
x1 <- c(1:1000)*runif(n=1000)
x2 <- (c(1:1000)*rnorm(n=1000))^2
x3 <- (c(1:1000)*rnorm(n=1000))^3

#fit multiple linear regression model
model <- lm(y~x1+x2+x3))

Modeldeki her tahmin değişkeni için kısmi artık grafikleri oluşturmak amacıyla R’deki araba paketindeki crPlots() işlevini kullanabiliriz:

 library (car)

#create partial residual plots
crPlots(model)

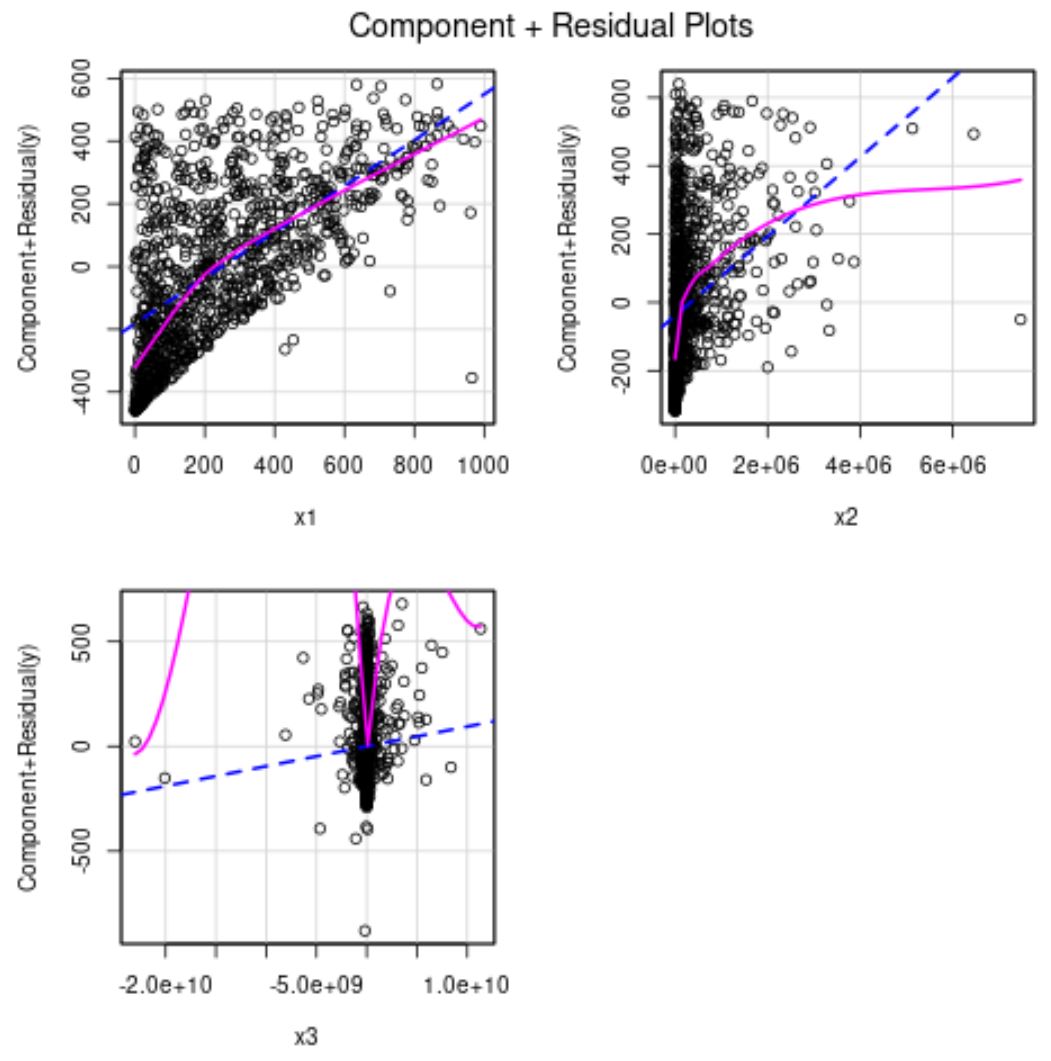
Mavi çizgi, yordayıcı ile yanıt değişkeni arasındaki ilişkinin doğrusal olması durumunda beklenen artıkları gösterir. Pembe çizgi gerçek artıkları gösterir.

İki çizgi önemli ölçüde farklıysa, bu doğrusal olmayan bir ilişkiye işaret eder.

Yukarıdaki grafiklerden x2 ve x3’e ait artıkların doğrusal olmadığını görebiliriz.

Bu, çoklu doğrusal regresyonun doğrusallık varsayımını ihlal eder. Bu sorunu çözmenin bir yolu, tahmin değişkenleri üzerinde kare veya kübik kök dönüşümü kullanmaktır:

 library (car)

#fit new model with transformed predictor variables
model_transformed <- lm(y~x1+sqrt(x2)+log10(x3^(1/3)))

#create partial residual plots for new model
crPlots(model_transformed)

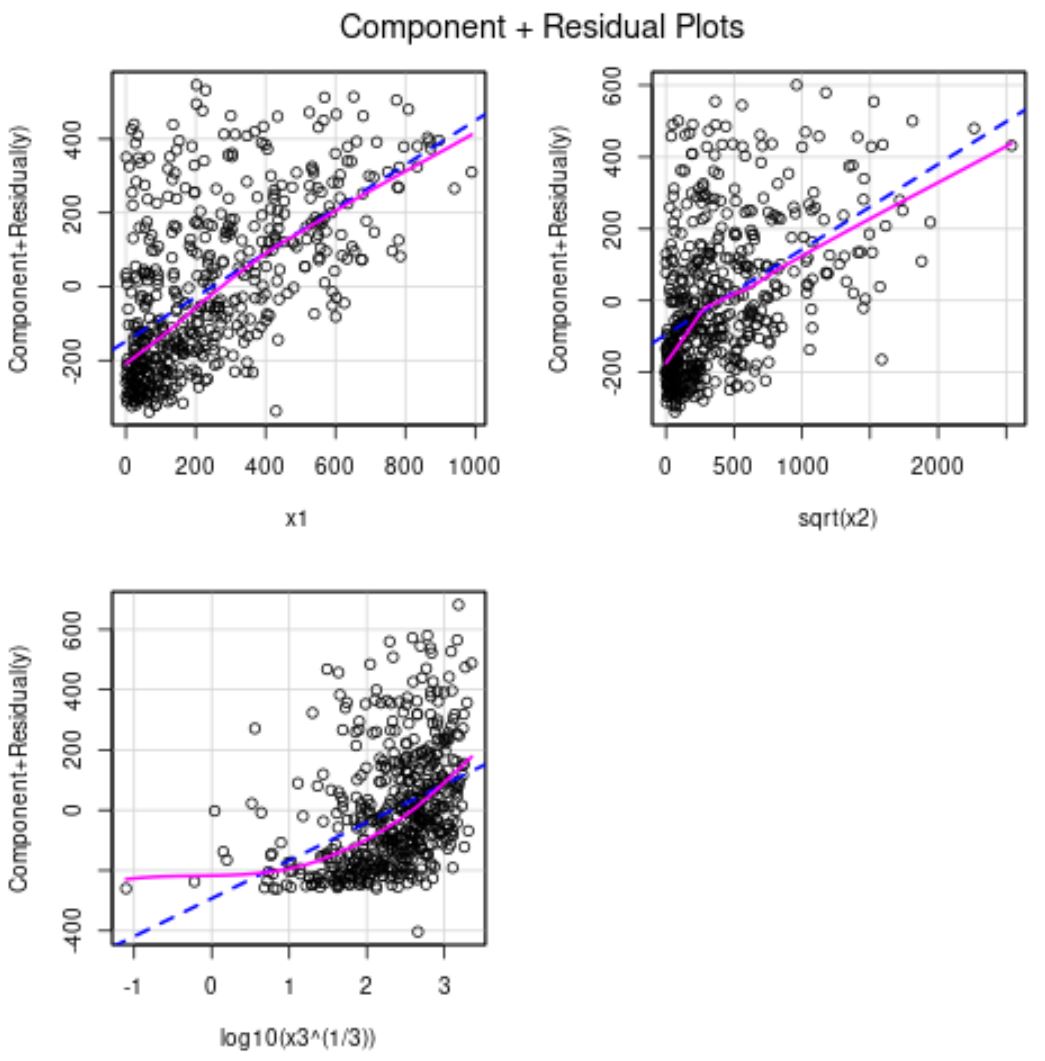
Kısmi artık grafiklerinden x2’nin artık yanıt değişkeniyle daha doğrusal bir ilişkiye sahip olduğunu görebiliriz.

x3 tahmin değişkeni hala bir şekilde doğrusal değildir, dolayısıyla başka bir dönüşüm denemeye veya muhtemelen değişkeni modelden tamamen çıkarmaya karar verebiliriz.

Ek kaynaklar

Aşağıdaki eğitimlerde R’de diğer ortak grafiklerin nasıl oluşturulacağı açıklanmaktadır:

R’de teşhis grafikleri nasıl oluşturulur
R’de ölçek ve konum grafiği nasıl oluşturulur
R’de artık arsa nasıl oluşturulur