R'de kısmi en küçük kareler (adım adım)

Makine öğreniminde karşılaşacağınız en yaygın sorunlardan biri çoklu bağlantıdır . Bu, bir veri setindeki iki veya daha fazla öngörücü değişkenin yüksek düzeyde korelasyona sahip olması durumunda ortaya çıkar.

Bu olduğunda, bir model bir eğitim veri setine iyi uyum sağlayabilir, ancak eğitim veri setine fazla uyum sağladığı için daha önce görmediği yeni bir veri setinde düşük performans gösterebilir. Eğitim Seti.

Bu sorunu aşmanın bir yolu , kısmi en küçük kareler adı verilen ve şu şekilde çalışan bir yöntem kullanmaktır:

• Tahmin edici ve yanıt değişkenlerini standartlaştırın.
• Hem yanıt değişkenindeki hem de yordayıcı değişkenlerdeki önemli miktarda varyasyonu açıklayan p orijinal yordayıcı değişkenin M doğrusal kombinasyonunu (“PLS bileşenleri” olarak adlandırılır) hesaplayın .
• Tahmin edici olarak PLS bileşenlerini kullanarak doğrusal bir regresyon modeline uymak için en küçük kareler yöntemini kullanın.
• Modelde tutulacak en uygun PLS bileşeni sayısını bulmak için k-katlı çapraz doğrulamayı kullanın .

Bu eğitimde, R’de kısmi en küçük karelerin nasıl gerçekleştirileceğine ilişkin adım adım bir örnek sunulmaktadır.

Adım 1: Gerekli paketleri yükleyin

R’de kısmi en küçük kareler gerçekleştirmenin en kolay yolu pls paketindeki işlevleri kullanmaktır.

 #install pls package (if not already installed)
install.packages(" pls ")

load pls package
library(pls)

Adım 2: Kısmi en küçük kareler modelini yerleştirin

Bu örnek için, farklı araba türlerine ilişkin verileri içeren mtcars adı verilen yerleşik R veri kümesini kullanacağız:

 #view first six rows of mtcars dataset
head(mtcars)

                   mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1

Bu örnek için, yanıt değişkeni olarak hp’yi ve tahmin değişkenleri olarak aşağıdaki değişkenleri kullanarak kısmi en küçük kareler (PLS) modelini uygulayacağız:

• mpg
• görüntülemek
• bok
• ağırlık
• qsec

Aşağıdaki kod, PLS modelinin bu verilere nasıl sığdırılacağını gösterir. Aşağıdaki argümanlara dikkat edin:

• ölçek=DOĞRU : Bu, R’ye, veri kümesindeki değişkenlerin her birinin ortalaması 0 ve standart sapması 1 olacak şekilde ölçeklendirilmesi gerektiğini söyler. Bu, farklı birimlerle ölçüldüğünde hiçbir yordayıcı değişkenin modelde çok fazla etkiye sahip olmamasını sağlar.
• validation=”CV” : Bu, R’ye model performansını değerlendirmek için k-katlı çapraz doğrulama kullanmasını söyler. Bunun varsayılan olarak k=10 kat kullandığını unutmayın. Ayrıca Birini Dışarıda Bırakma çapraz doğrulaması gerçekleştirmek yerine “LOOCV”yi belirtebileceğinizi de unutmayın.

 #make this example reproducible
set.seed(1)

#fit PCR model
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale= TRUE , validation=" CV ")

Adım 3: PLS bileşenlerinin sayısını seçin

Modeli yerleştirdikten sonra kaç tane PLS bileşeni tutacağımızı belirlememiz gerekiyor.

Bunu yapmak için k-çapraz doğrulamayla hesaplanan test kök ortalama kare hatasına (test RMSE) bakmanız yeterlidir:

 #view summary of model fitting
summary(model)

Data: 
	Y dimension: 32 1
Fit method: kernelpls
Number of components considered: 5

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept) 1 comp 2 comps 3 comps 4 comps 5 comps
CV 69.66 40.57 35.48 36.22 36.74 36.67
adjCV 69.66 40.41 35.12 35.80 36.27 36.20

TRAINING: % variance explained
    1 comp 2 comps 3 comps 4 comps 5 comps
X 68.66 89.27 95.82 97.94 100.00
hp 71.84 81.74 82.00 82.02 82.03

Sonuçta iki ilginç tablo var:

1. DOĞRULAMA: RMSEP

Bu tablo bize k-katlı çapraz doğrulamayla hesaplanan RMSE testini anlatır. Aşağıdakileri görebiliriz:

• Modelde sadece orijinal terimi kullanırsak testin RMSE’si 69,66 olur.
• İlk PLS bileşenini de eklersek RMSE testi 40,57’ye düşüyor.
• İkinci PLS bileşenini de eklersek RMSE testi 35,48’e düşüyor.

Ek PLS bileşenlerinin eklenmesinin aslında testin RMSE’sinde artışa yol açtığını görebiliriz. Dolayısıyla nihai modelde yalnızca iki PLS bileşeninin kullanılmasının optimal olacağı görülmektedir.

2. EĞİTİM: açıklanan varyans yüzdesi

Bu tablo bize PLS bileşenleri tarafından açıklanan yanıt değişkenindeki varyansın yüzdesini gösterir. Aşağıdakileri görebiliriz:

• Yalnızca ilk PLS bileşenini kullanarak yanıt değişkenindeki varyasyonun %68,66’sını açıklayabiliriz.
• İkinci PLS bileşenini ekleyerek yanıt değişkenindeki varyasyonun %89,27’sini açıklayabiliriz.

Daha fazla PLS bileşeni kullanarak hala daha fazla varyansı açıklayabileceğimizi unutmayın, ancak ikiden fazla PLS bileşeni eklemenin aslında açıklanan varyans yüzdesini çok fazla artırmadığını görebiliriz.

Validationplot() işlevini kullanarak RMSE testini (MSE ve R-kare testiyle birlikte) PLS bileşenlerinin sayısının bir fonksiyonu olarak da görselleştirebiliriz.

 #visualize cross-validation plots
validationplot(model)
validationplot(model, val.type=" MSEP ")
validationplot(model, val.type=" R2 ") 

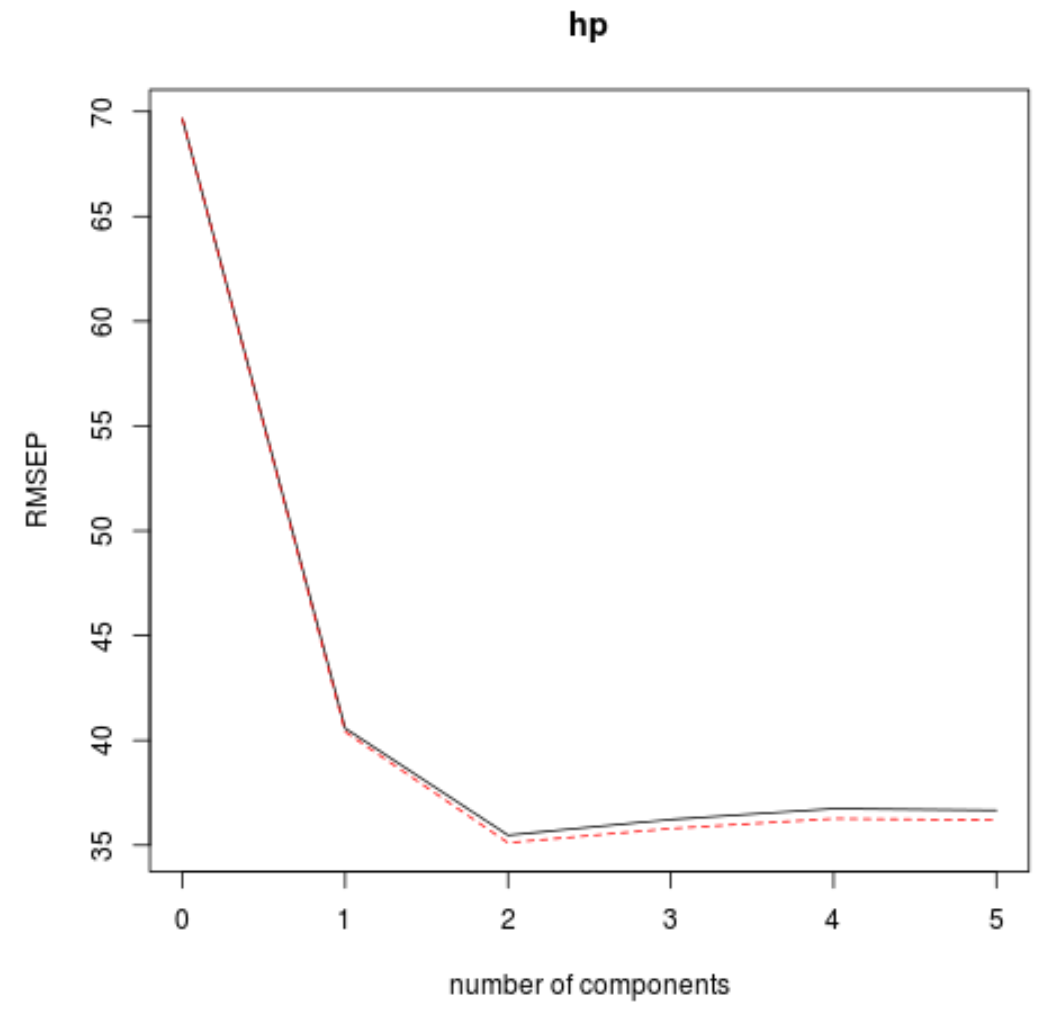
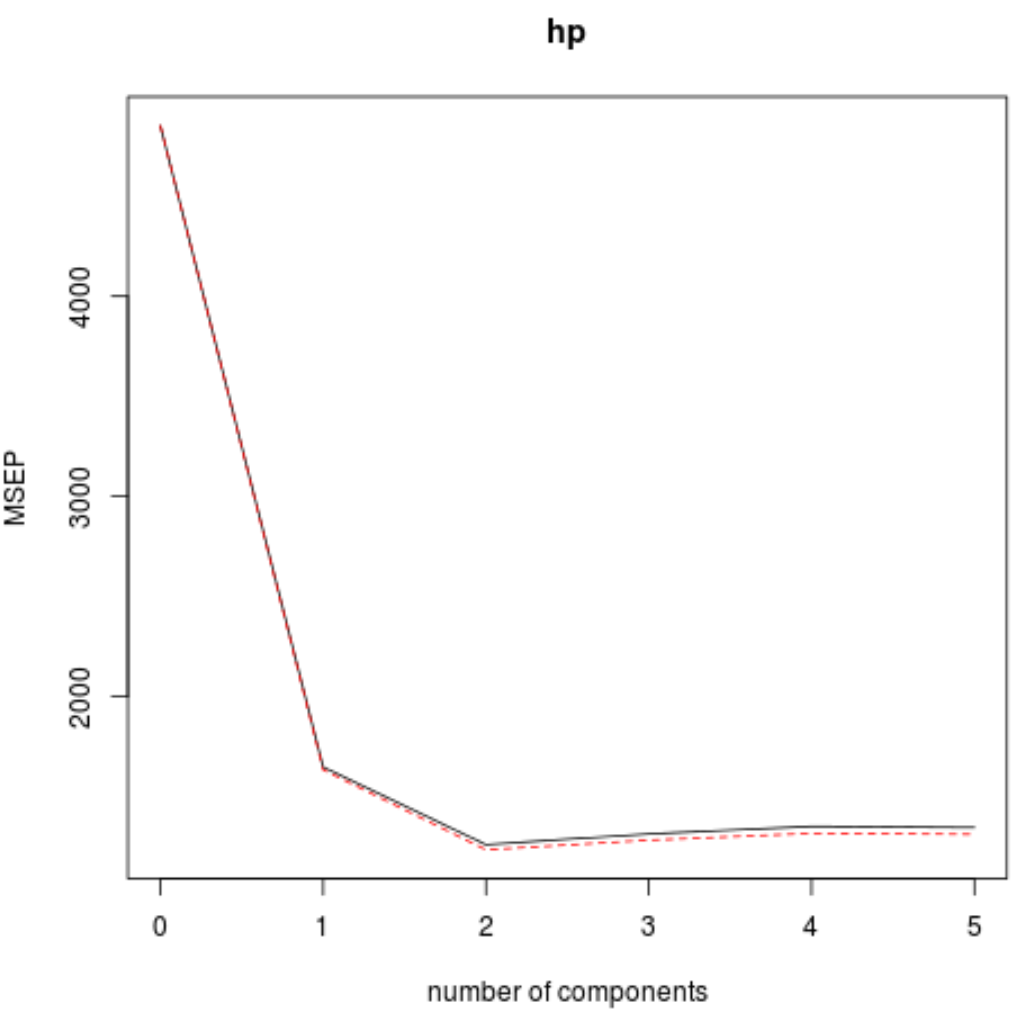
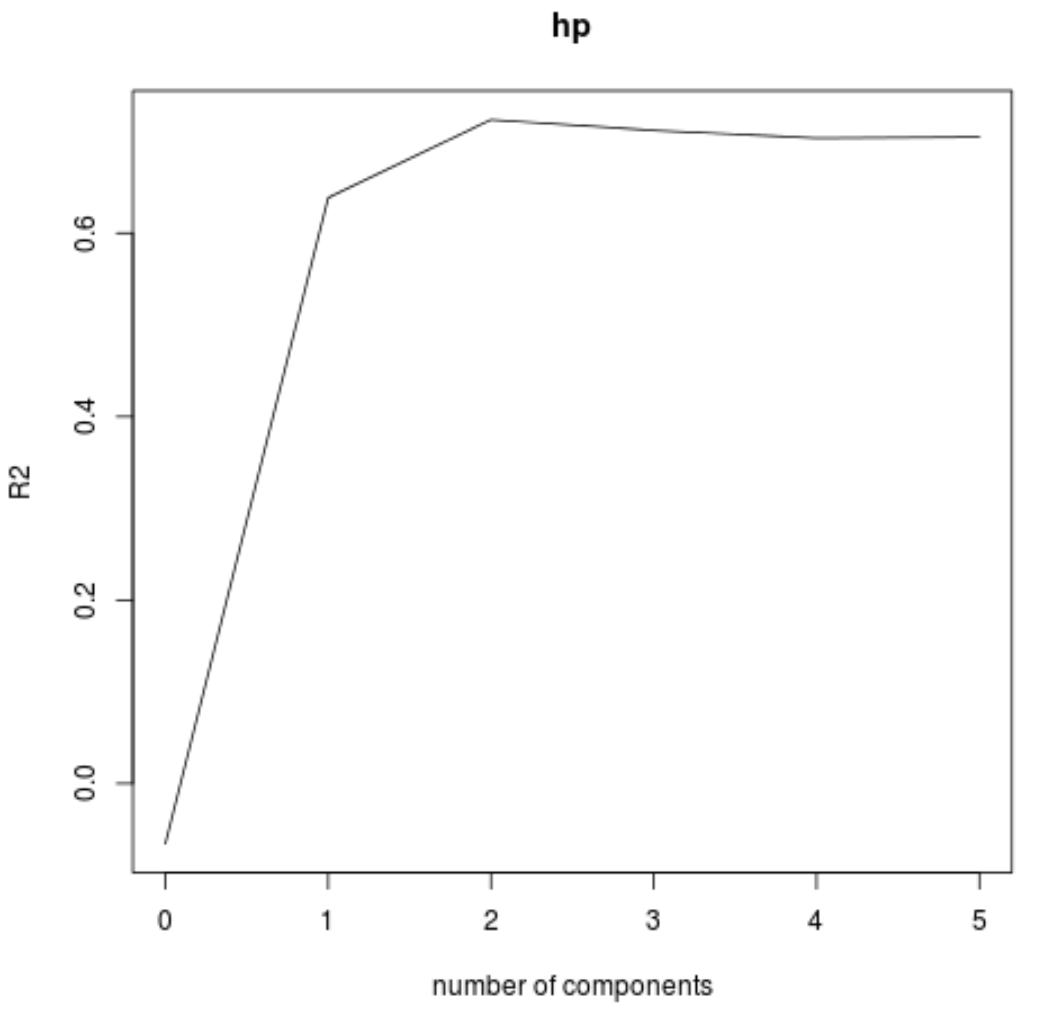
Her grafikte, iki PLS bileşeni eklendiğinde model uyumunun arttığını ancak daha fazla PLS bileşeni eklediğimizde bozulma eğiliminde olduğunu görebiliriz.

Bu nedenle optimal model yalnızca ilk iki PLS bileşenini içerir.

Adım 4: Tahminlerde bulunmak için son modeli kullanın

Yeni gözlemler hakkında tahminlerde bulunmak için son modeli iki PLS bileşeniyle kullanabiliriz.

Aşağıdaki kod, orijinal veri kümesinin bir eğitim ve test kümesine nasıl bölüneceğini ve test kümesi üzerinde tahminler yapmak için iki PLS bileşeniyle son modelin nasıl kullanılacağını gösterir.

 #define training and testing sets
train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")]
y_test <- mtcars[26: nrow (mtcars), c("hp")]
test <- mtcars[26: nrow (mtcars), c("mpg", "disp", "drat", "wt", "qsec")]
    
#use model to make predictions on a test set
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=train, scale= TRUE , validation=" CV ")
pcr_pred <- predict(model, test, ncomp= 2 )

#calculate RMSE
sqrt ( mean ((pcr_pred - y_test)^2))

[1] 54.89609

Testin RMSE’sinin 54,89609 olduğunu görüyoruz. Bu, test seti gözlemleri için tahmin edilen hp değeri ile gözlenen hp değeri arasındaki ortalama sapmadır.

İki temel bileşene sahip eşdeğer bir temel bileşenler regresyon modelinin 56,86549 değerinde bir test RMSE’si ürettiğini unutmayın. Dolayısıyla PLS modeli bu veri seti için PCR modelinden biraz daha iyi performans gösterdi.

Bu örnekteki R kodunun tam kullanımını burada bulabilirsiniz.