R'de korelasyon testi nasıl yapılır (örneklerle)

İki değişken arasındaki ilişkiyi ölçmenin bir yolu, iki değişken arasındaki doğrusal ilişkinin bir ölçüsü olan Pearson korelasyon katsayısını kullanmaktır .

Her zaman -1 ile 1 arasında bir değer alır; burada:

• -1, iki değişken arasında tamamen negatif bir doğrusal korelasyonu gösterir
• 0, iki değişken arasında doğrusal bir korelasyon olmadığını gösterir
• 1, iki değişken arasında mükemmel pozitif doğrusal bir korelasyonu gösterir

Bir korelasyon katsayısının istatistiksel olarak anlamlı olup olmadığını belirlemek için karşılık gelen t-puanını ve p-değerini hesaplayabilirsiniz.

Korelasyon katsayısının (r) t-puanını hesaplama formülü şöyledir:

t = r * √ n-2 / √ 1-r ²

P-değeri, n-2 serbestlik derecesine sahip t-dağılımı için karşılık gelen iki kuyruklu p-değeri olarak hesaplanır.

Örnek: R’de korelasyon testi

İki değişken arasındaki korelasyon katsayısının istatistiksel olarak anlamlı olup olmadığını belirlemek için aşağıdaki sözdizimini kullanarak R’de bir korelasyon testi gerçekleştirebilirsiniz:

cor.test(x, y, method=c(“pearson”, “kendall”, “mızrakçı”))

Altın:

• x, y: dijital veri vektörleri.
• yöntem: İki vektör arasındaki korelasyonu hesaplamak için kullanılan yöntem. Varsayılan “Pearson”dur.

Örneğin, R’de aşağıdaki iki vektöre sahip olduğumuzu varsayalım:

 x <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23)
y <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43)

İki değişken arasında korelasyon testi yapmadan önce ilişkilerini görselleştirmek için hızlı bir dağılım grafiği oluşturabiliriz:

 #create scatterplot
plot(x, y, pch= 16 )

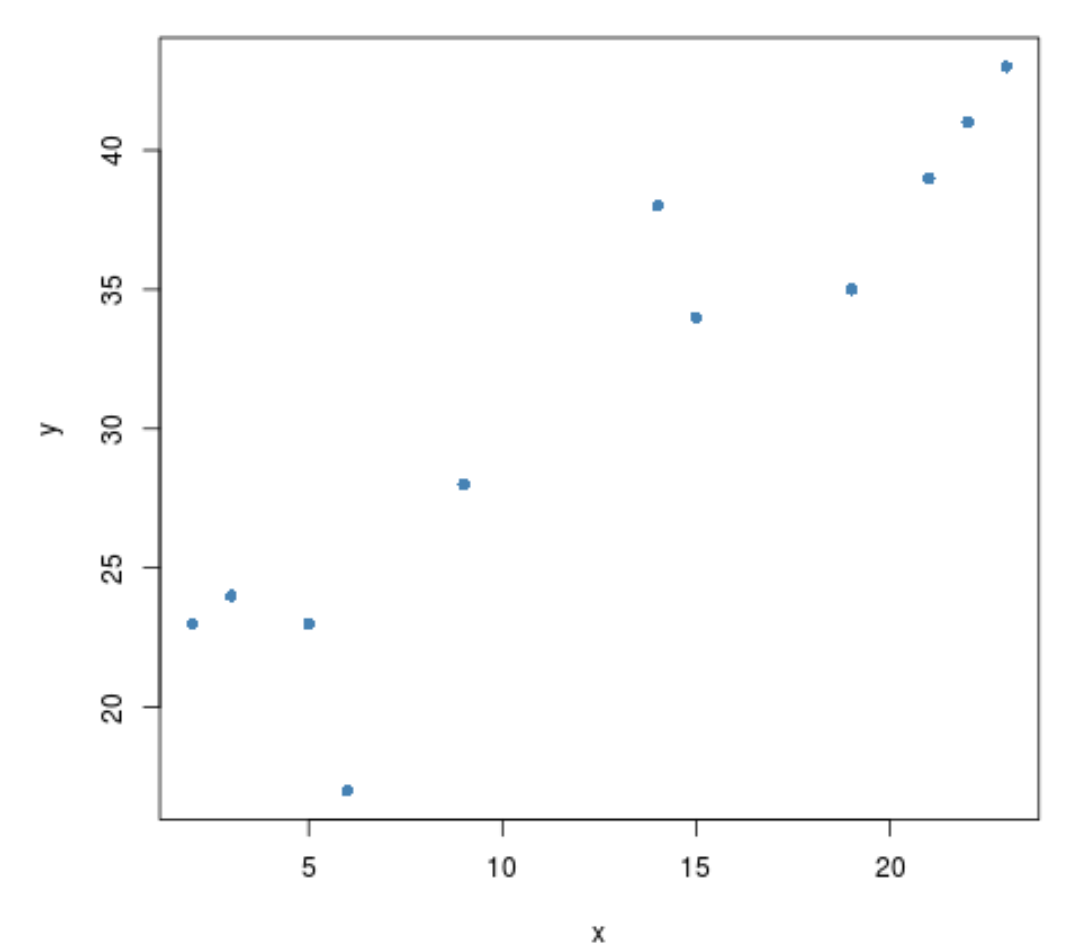
İki değişken arasında pozitif bir ilişkinin olduğu görülmektedir. Yani biri arttıkça diğeri de artma eğilimindedir.

Bu korelasyonun istatistiksel olarak anlamlı olup olmadığını görmek için bir korelasyon testi yapabiliriz:

 #perform correlation test between the two vectors
cor.test(x, y)

	Pearson's product-moment correlation

data: x and y
t = 7.8756, df = 10, p-value = 1.35e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7575203 0.9799783
sample estimates:
      horn 
0.9279869

İki vektör arasındaki korelasyon katsayısı 0,9279869 olarak ortaya çıkıyor.

Test istatistiği 7,8756 ve buna karşılık gelen p değeri 1,35e-05 olarak ortaya çıkıyor.

Bu değer 0,05’ten küçük olduğundan iki değişken arasındaki ilişkinin istatistiksel olarak anlamlı olduğunu söyleyebilecek yeterli kanıtımız vardır.

Ek kaynaklar

Aşağıdaki eğitimler korelasyon katsayıları hakkında ek bilgi sağlar:

Pearson Korelasyon Katsayısına Giriş
“Güçlü” bir korelasyon olarak kabul edilen şey nedir?
Pearson korelasyonunun beş hipotezi