R'de normallik nasıl test edilir (4 yöntem)

Birçok istatistiksel test, veri setlerinin normal şekilde dağıldığını varsayar .

R’de bu varsayımı kontrol etmenin dört yaygın yolu vardır:

1. (Görsel yöntem) Bir histogram oluşturun.

• Histogram yaklaşık olarak “çan” şeklindeyse verilerin normal dağıldığı varsayılır.

2. (Görsel yöntem) Bir QQ grafiği oluşturun.

• Grafikteki noktalar kabaca düz bir çapraz çizgi boyunca uzanıyorsa, verilerin normal dağıldığı varsayılır.

3. (Resmi istatistiksel test) Shapiro-Wilk testi yapın.

• Testin p değeri α = 0,05’ten büyükse verilerin normal dağıldığı varsayılır.

4. (Resmi istatistiksel test) Kolmogorov-Smirnov testini yapın.

• Testin p değeri α = 0,05’ten büyükse verilerin normal dağıldığı varsayılır.

Aşağıdaki örnekler bu yöntemlerin her birinin pratikte nasıl kullanılacağını göstermektedir.

Yöntem 1: Histogram Oluşturma

Aşağıdaki kod, R’de normal olarak dağıtılan ve normal olarak dağıtılmayan bir veri kümesi için histogramın nasıl oluşturulacağını gösterir:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create histogram for both datasets
hist(normal_data, col=' steelblue ', main=' Normal ')
hist(non_normal_data, col=' steelblue ', main=' Non-normal ') 

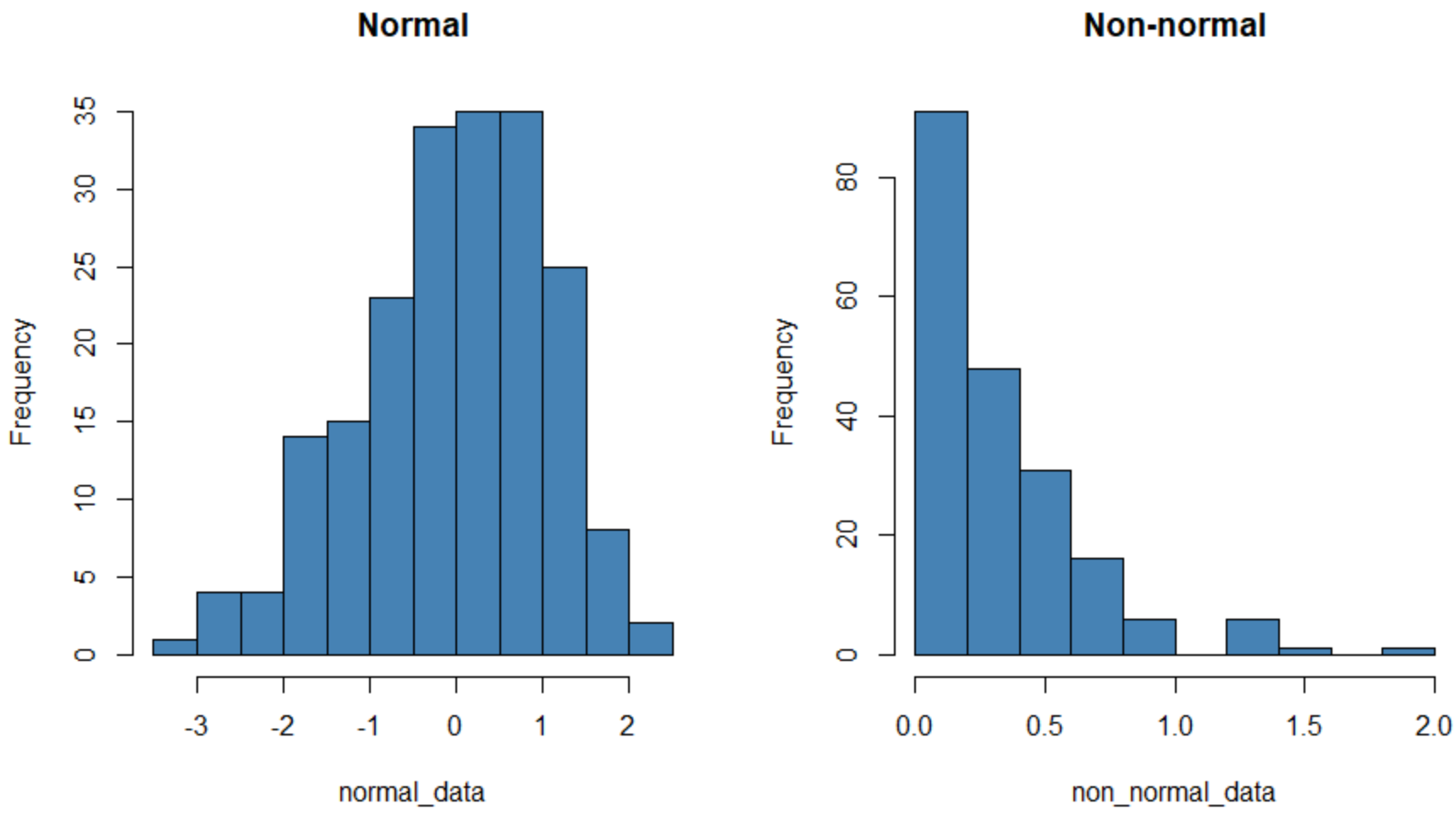
Soldaki histogram normal olarak dağılan bir veri setini (kabaca “çan” şeklinde) gösterirken sağdaki histogram normal olarak dağılmayan bir veri setini gösterir.

Yöntem 2: QQ Grafiği Oluşturma

Aşağıdaki kod, R’de normal olarak dağıtılan ve normal olarak dağıtılmayan bir veri kümesi için QQ grafiğinin nasıl oluşturulacağını gösterir:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create QQ plot for both datasets
qqnorm(normal_data, main=' Normal ')
qqline(normal_data)

qqnorm(non_normal_data, main=' Non-normal ')
qqline(non_normal_data)

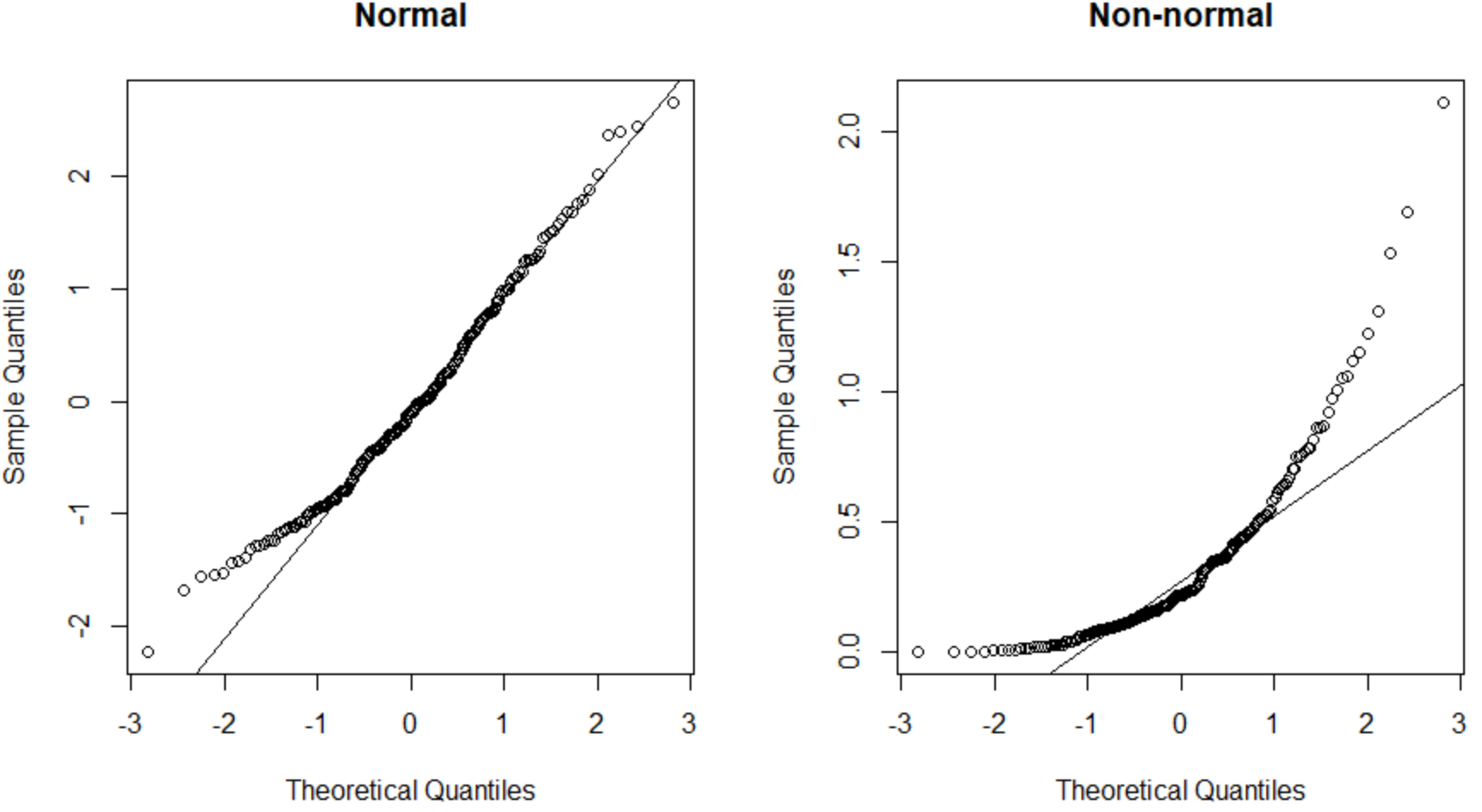
Soldaki QQ grafiği, normal olarak dağıtılan bir veri kümesini sunar (noktalar düz bir çapraz çizgi boyunca düşer) ve sağdaki QQ grafiği, normal şekilde dağıtılmayan bir veri kümesini sunar.

Yöntem 3: Shapiro-Wilk testi gerçekleştirin

Aşağıdaki kod, R’de normal olarak dağıtılan ve normal olarak dağıtılmayan bir veri kümesi üzerinde Shapiro-Wilk testinin nasıl gerçekleştirileceğini gösterir:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform shapiro-wilk test
shapiro. test (normal_data)

	Shapiro-Wilk normality test

data: normal_data
W = 0.99248, p-value = 0.3952

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform shapiro-wilk test
shapiro. test (non_normal_data)

	Shapiro-Wilk normality test

data: non_normal_data
W = 0.84153, p-value = 1.698e-13

İlk testin p değerinin 0,05’ten küçük olmaması verilerin normal dağıldığını gösterir.

İkinci testin p değerinin 0,05’ten küçük olması verilerin normal dağılmadığını göstermektedir.

Yöntem 4: Kolmogorov-Smirnov testi yapın

Aşağıdaki kod, R’de normal olarak dağıtılan ve normal olarak dağıtılmayan bir veri kümesi üzerinde Kolmogorov-Smirnov testinin nasıl gerçekleştirileceğini gösterir:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform kolmogorov-smirnov test
ks. test (normal_data, ' pnorm ')

	One-sample Kolmogorov–Smirnov test

data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform kolmogorov-smirnov test
ks. test (non_normal_data, ' pnorm ') 
	One-sample Kolmogorov–Smirnov test

data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided

İlk testin p değerinin 0,05’ten küçük olmaması verilerin normal dağıldığını gösterir.

İkinci testin p değerinin 0,05’ten küçük olması verilerin normal dağılmadığını göstermektedir.

Normal olmayan veriler nasıl işlenir?

Belirli bir veri kümesi normal şekilde dağılmıyorsa , onu daha normal bir şekilde dağıtmak için genellikle aşağıdaki dönüşümlerden birini gerçekleştirebiliriz:

1. Log dönüşümü: x değerlerini log(x)’ e dönüştürün.

2. Karekök dönüşümü: x’in değerlerini √x’e dönüştürün.

3. Küp kök dönüşümü: x’in değerlerini x ^1/3’e dönüştürün.

Bu dönüşümlerin gerçekleştirilmesiyle veri kümesi genel olarak daha normal dağılmış hale gelir.

Bu dönüşümlerin R’de nasıl gerçekleştirileceğini görmek için bu eğitimi okuyun.

Ek kaynaklar

R’de histogramlar nasıl oluşturulur
R’de QQ grafiği nasıl oluşturulur ve yorumlanır
R’de Shapiro-Wilk testi nasıl yapılır
R’de Kolmogorov-Smirnov testi nasıl yapılır?