R'de önyükleme nasıl yapılır (örneklerle)

Önyükleme, herhangi bir istatistiğin standart hatasını tahmin etmek ve istatistik için birgüven aralığı oluşturmak için kullanılabilecek bir yöntemdir.

Önyükleme için temel süreç aşağıdaki gibidir:

• Belirli bir veri kümesinden değiştirilerek k adet kopya örnek alın.
• Her örnek için ilgilenilen istatistiği hesaplayın.
• Bu, belirli bir istatistik için k farklı tahmin verir; bunu daha sonra istatistiğin standart hatasını hesaplamak ve istatistik için bir güven aralığı oluşturmak için kullanabilirsiniz.

Bootstrap kütüphanesindeki aşağıdaki işlevleri kullanarak R’de önyükleme yapabiliriz:

1. Önyükleme örnekleri oluşturun.

önyükleme (veri, istatistik, R,…)

Altın:

• veri: bir vektör, matris veya veri bloğu
• istatistik: başlatılacak istatistikleri üreten bir fonksiyon
• A: Önyükleme tekrarlarının sayısı

2. Bir önyükleme güven aralığı oluşturun.

boot.ci(önyükleme nesnesi, yapılandırma, tür)

Altın:

• bootobject: Boot() işlevi tarafından döndürülen bir nesne
• conf: Hesaplanacak güven aralığı. Varsayılan değer 0,95’tir
• tür: Hesaplanacak güven aralığı türü. Seçenekler arasında ‘standart’, ‘temel’, ‘saplama’, ‘perc’, ‘bca’ ve ‘tümü’ yer alır – varsayılan olarak ‘tümü’

Aşağıdaki örnekler bu fonksiyonların pratikte nasıl kullanılacağını göstermektedir.

Örnek 1: tek bir istatistiği önyükleme

Aşağıdaki kod, basit bir doğrusal regresyon modelinin R-karesine ilişkin standart hatanın nasıl hesaplanacağını gösterir:

 set.seed(0)
library (boot)

#define function to calculate R-squared
rsq_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (summary(fit)$r.square) #return R-squared of model
}
#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=rsq_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = rsq_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
     original bias std. error
t1* 0.7183433 0.002164339 0.06513426

Sonuçlardan şunları görebiliriz:

• Bu regresyon modelinin tahmini R-kare değeri 0,7183433’tür .
• Bu tahminin standart hatası 0,06513426’dır .

Ayrıca ön yüklemeli örneklerin dağılımını da hızlı bir şekilde görselleştirebiliyoruz:

 plot(reps)

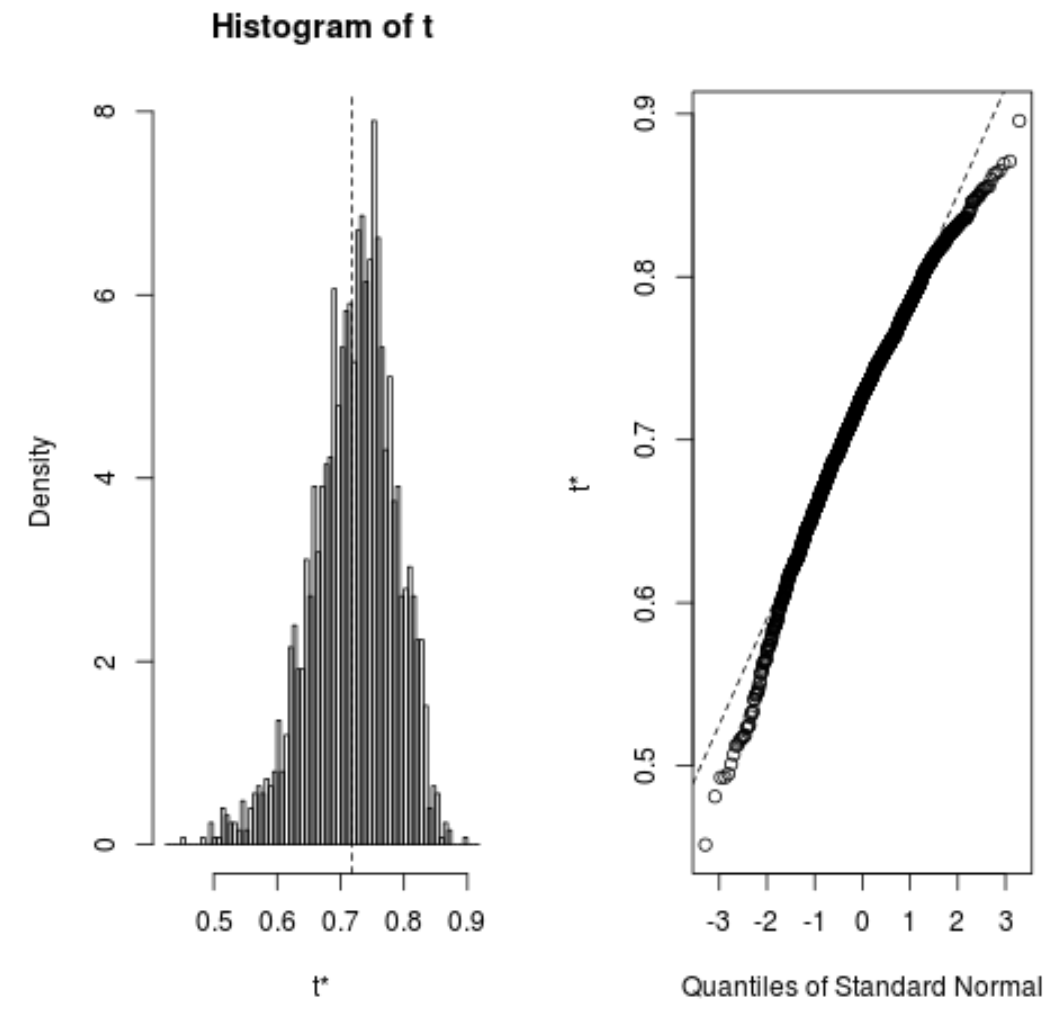
Modelin tahmini R-karesine ilişkin %95 güven aralığını hesaplamak için aşağıdaki kodu da kullanabiliriz:

 #calculate adjusted bootstrap percentile (BCa) interval
boot.ci(reps, type=" bca ")

CALL: 
boot.ci(boot.out = reps, type = "bca")

Intervals: 
Level BCa          
95% (0.5350, 0.8188)  
Calculations and Intervals on Original Scale

Sonuçtan, gerçek R-kare değerleri için önyüklemeli %95 güven aralığının (0,5350, 0,8188) olduğunu görebiliriz.

Örnek 2: birden fazla istatistiği önyükleme

Aşağıdaki kod, çoklu doğrusal regresyon modelinde her katsayı için standart hatanın nasıl hesaplanacağını gösterir:

 set.seed(0)
library (boot)

#define function to calculate fitted regression coefficients
coef_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (coef(fit)) #return coefficient estimates of model
}

#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=coef_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = coef_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
       original bias std. error
t1* 29.59985476 -5.058601e-02 1.49354577
t2* -0.04121512 6.549384e-05 0.00527082

Sonuçlardan şunları görebiliriz:

• Model kesişimi için tahmin edilen katsayı 29,59985476 ve bu tahminin standart hatası 1,49354577’dir .
• Modeldeki yordayıcı değişken disp’nin tahmin edilen katsayısı -0,04121512 ve bu tahminin standart hatası 0,00527082’dir .

Ayrıca ön yüklemeli örneklerin dağılımını da hızlı bir şekilde görselleştirebiliyoruz:

 plot(reps, index=1) #intercept of model
plot(reps, index=2) #disp predictor variable

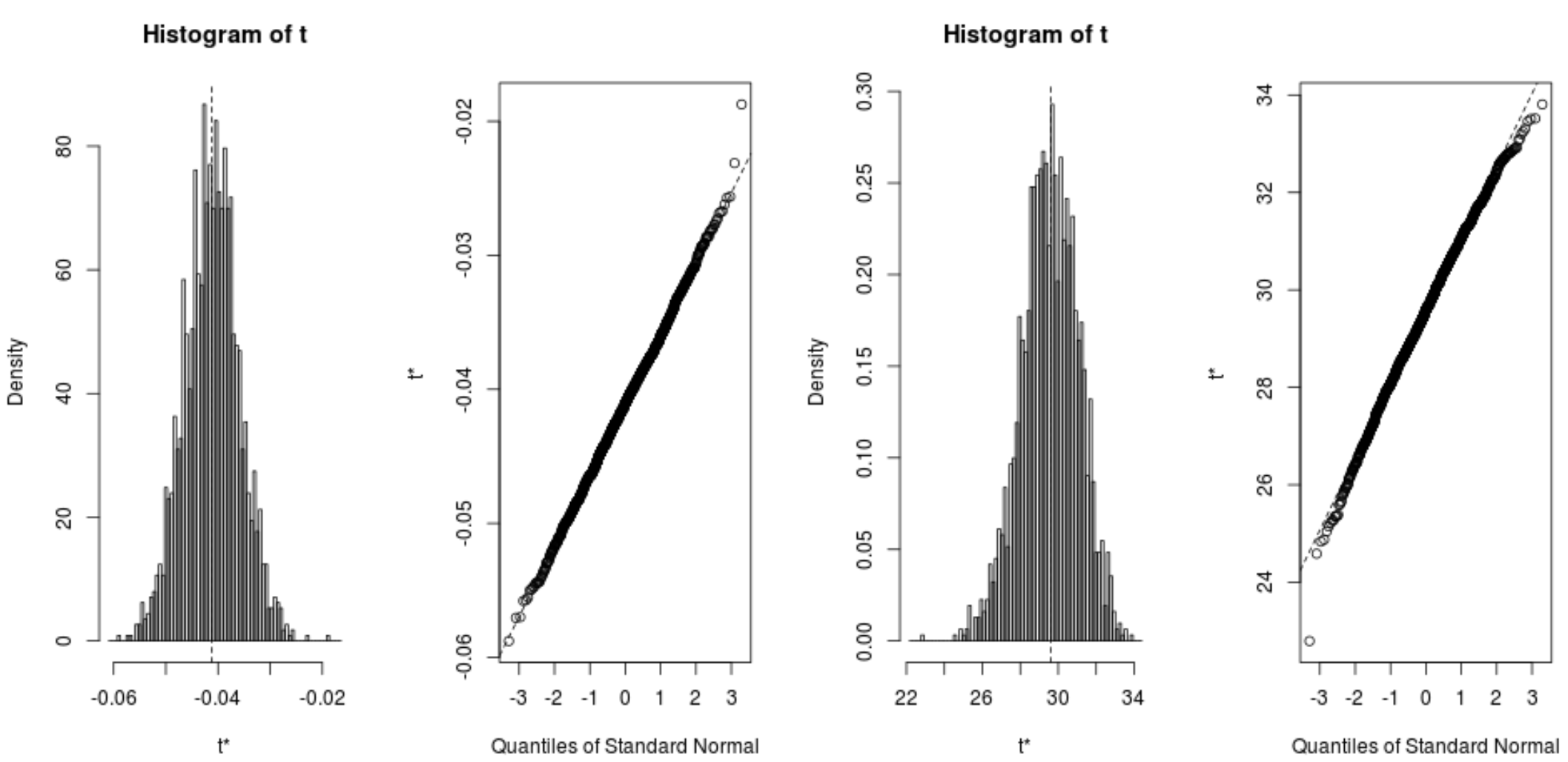
Her katsayının %95 güven aralıklarını hesaplamak için aşağıdaki kodu da kullanabiliriz:

 #calculate adjusted bootstrap percentile (BCa) intervals
boot.ci(reps, type=" bca ", index=1) #intercept of model
boot.ci(reps, type=" bca ", index=2) #disp predictor variable

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 1)

Intervals: 
Level BCa          
95% (26.78, 32.66)  
Calculations and Intervals on Original Scale
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 2000 bootstrap replicates

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 2)

Intervals: 
Level BCa          
95% (-0.0520, -0.0312)  
Calculations and Intervals on Original Scale

Sonuçlardan, model katsayıları için önyüklemeli %95 güven aralıklarının aşağıdaki gibi olduğunu görebiliriz:

• Müdahale için IC: (26,78, 32,66)
• Dağıtım için CI: (-.0520, -.0312)

Ek kaynaklar

R’de basit doğrusal regresyon nasıl gerçekleştirilir
R’de çoklu doğrusal regresyon nasıl gerçekleştirilir
Güven Aralıklarına Giriş